개별항 이항 분포 확률을 반환합니다. 고정된 횟수의 검정이나 시행을 거치는 문제에서 시행의 결과값이 성공 또는 실패 중 하나이고, 시행이 서로 독립적이며, 성공 확률이 전체 실험에서 일정하게 나타나는 경우 BINOMDIST 함수를 사용합니다. 예를 들어 앞으로 태어날 세 명의 아기 중 두 명이 남자 아기일 확률을 계산할 때 이 함수를 사용할 수 있습니다.
중요: 이 함수는 보다 정확하고 이름에서 용도를 짐작할 수 있는 하나 이상의 새 함수로 대체되었습니다. 이전 Excel 버전과의 호환성을 위해 이러한 함수를 계속 사용할 수 있지만, 이후 버전의 Excel에서는 사용하지 못할 수 있으므로 지금부터 새 함수를 사용하는 것이 좋습니다.
새 함수에 대한 자세한 내용은 BINOM.DIST 함수를 참조하세요.
구문
BINOMDIST(number_s,trials,probability_s,cumulative)
BINOMDIST 함수 구문에는 다음과 같은 인수가 사용됩니다.
-
number_s 필수 요소입니다. 시행에서의 성공 횟수입니다.
-
trials 필수 요소입니다. 독립 시행 횟수입니다.
-
probability_s 필수 요소입니다. 각 시행에서 성공할 확률입니다.
-
cumulative 필수 요소입니다. 함수의 형식을 결정하는 논리 값입니다. 누적이 TRUE이면 BINOMDIST는 최대 number_s 성공이 있을 확률인 누적 분포 함수를 반환합니다. FALSE이면 성공 가능성이 number_s 확률 질량 함수를 반환합니다.
주의
-
number_s 및 trials는 정수로 변환되며 소수점 이하는 무시됩니다.
-
number_s, trials 또는 probability_s가 숫자가 아니면 BINOMDIST에서는 #VALUE! 오류 값이 반환됩니다.
-
number_s < 0 또는 number_s > trials이면 BINOMDIST에서는 #NUM! 오류 값이 반환됩니다.
-
probability_s < 0 또는 probability_s > 1이면 BINOMDIST에서는 #NUM! 오류 값이 반환됩니다.
-
x = number_s, n = trials이고 p = probability_s이면 이항 확률 질량 함수는 다음과 같습니다.
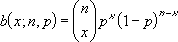
설명:

은 COMBIN(n,x)입니다.
-
x = number_s, n = trials 및 p = probability_s이면 누적 이항 분포는 다음과 같습니다.
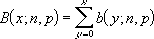
예제
다음 표의 예제 데이터를 복사하여 새 Excel 워크시트의 A1 셀에 붙여 넣습니다. 수식의 결과를 표시하려면 수식을 선택하고 F2 키를 누른 다음 Enter 키를 누릅니다. 필요한 경우 열 너비를 조정하면 데이터를 모두 표시할 수 있습니다.
|
데이터 |
설명 |
|
|
6 |
성공 횟수입니다. |
|
|
10 |
독립 시행 횟수입니다. |
|
|
0.5 |
각 시행의 성공 확률입니다. |
|
|
수식 |
설명 |
결과 |
|
=BINOMDIST(A2,A3,A4,FALSE) |
10회의 시행 중 정확히 6회가 성공할 확률입니다. |
0.2050781 |










