When you include multiple data sources in an Access query, you use joins to limit the records that you want to see, based on how the data sources are related to each other. You also use joins to combine records from both data sources, so that each pair of records from the sources becomes one record in the query results.
This article discusses the various types of joins and shows you how to use them in a query. By default, a join is automatically created if there is already a relationship between two data sources that you use in a query. A join is also created if there are fields that clearly correspond to each other. You can delete an automatically created join. This article provides basic information about table relationships, including how to create one.
Note: You can join queries in the same way that you join tables, and can also join both.
In this article
Overview
A database is a collection of tables of data that bear logical relationships to each other. You use relationships to connect tables by fields that they have in common. A table can be part of any number of relationships, but each relationship always has exactly two tables. In a query, a relationship is represented by a join.
When you add tables to a query, Access creates joins that are based on relationships that have been defined between the tables. You can manually create joins in queries, even if they do not represent relationships that have already been defined. If you use other queries (instead of or in addition to tables) as sources of data for a query, you can create joins between the source queries, and also between those queries and any tables that you use as sources of data.
Joins behave similarly to query criteria in that they establish rules that the data must match to be included in the query operations. Unlike criteria, joins also specify that each pair of rows that satisfy the join conditions will be combined in the recordset to form a single row.
There are four basic types of joins: inner joins, outer joins, cross joins, and unequal joins. This article explores each type of join you can use, why you use each type, and how to create the joins.
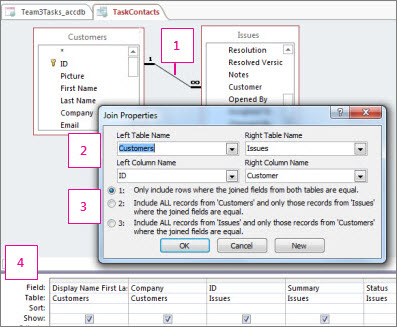
Joins are to queries what relationships are to tables: an indication of how data in two sources can be combined based on data values they have in common. Here’s an illustration of a join in query Design View, with the join’s properties open in a dialog box:
This line between the tables represents the join. Double-click a join to open the Join Properties dialog box (depicted) and review or change the join.
Joins are sometimes directional. This area of the dialog box shows you which table is which in the join, and which fields are used to join the tables.
This area determines the type of join: option 1 is an inner join, 2 is a left outer join, and 3 is a right outer join.
Fields from both tables can be used, and data that pertains to a given task is displayed from each. In an inner join, no other data is included. In an outer join, unrelated records from one table are also included in the query results.
Types of joins
There are four basic types of joins: inner joins, outer joins, cross joins, and unequal joins. Cross joins and unequal joins are advanced join types and are rarely used, but you should know about them to have a full understanding of how joins work.
Inner joins: only related data from both tables combined
An inner join is one in which Access only includes data from a table if there is corresponding data in the related table, and vice versa. Most of the time, you will use inner joins. When you create a join and don’t specify what kind of join it is, Access assumes you want an inner join. Inner joins are useful because they let you combine data from two sources based on shared values – so you only see data when there’s a complete picture.
Outer joins: all the related data combined correctly, plus all the remaining records from one table
An outer join is like an inner join, but adds the remaining rows from one of the tables. Outer joins are directional: a left outer join includes all the records from the left table – the first table in the join – and a right outer join includes all the records from the right table – the second table in the join.
Full outer joins: all the data, combined where feasible
In some systems, an outer join can include all rows from both tables, with rows combined when they correspond. This is called a full outer join, and Access doesn’t explicitly support them. However, you can use a cross join and criteria to achieve the same effect.
Cross joins: all the data, combined every possible way
Most of the time, a cross join is a side effect of adding two tables to a query and then forgetting to join them. Access interprets this to mean that you want to see every record from one table combined with every record from the other table – every possible combination of records. Because no data can be combined, this kind of join rarely produces useful results. But there are a few cases when a cross join is just what you need.
Unequal joins: like a regular join, but using a different comparison to combine rows
Unequal joins use an operator other than the equal sign (=) to compare values and determine whether and how to combine the data. Unequal joins aren’t explicitly supported, but you can use a cross join and criteria to achieve the same effect.
Show rows where a common value exists in both of the joined tables
If you want to show only those rows that have matching values in the joined field, you use an inner join. Access creates inner joins automatically.
Inner joins are the most common type of join. They tell a query that rows from one of the joined tables correspond to rows in the other table, on the basis of the data in the joined fields. When a query with an inner join is run, only those rows where a common value exists in both of the joined tables will be included in the query operations.
How do I use an inner join?
Most of the time, you don't need to do anything to use an inner join. If the tables that you add to a query already have relationships, Access automatically creates an inner join between each pair of related tables, when you add the tables. If referential integrity is enforced, Access also displays a "1" above the join line to show which table is on the "one" side of a one-to-many relationship and an infinity symbol (∞) to show which table is on the "many" side.
Even if you haven't created relationships, Access automatically creates inner joins if you add two tables to a query and those tables each have a field with the same or compatible data type and one of the join fields is a primary key. The "one" and "many" symbols are not displayed in this case, because referential integrity is not enforced.
If you add queries to your query, and have not created relationships between those queries, Access does not automatically create inner joins between those queries or between queries and tables. Generally, you should create them yourself. You create an inner join by dragging a field from one data source to a field on another data source. Access displays a line between the two fields to show that a join has been created.
SQL syntax for an inner join
Inner joins are specified in SQL in the FROM clause, as shown below:
FROM table1 INNER JOIN table2 ON table1.field1 compare table2.field2
The INNER JOIN operation has these parts:
|
Part |
Description |
|
table1, table2 |
The names of the tables from which records are combined. |
|
field1, field2 |
The names of the fields that are joined. If they are not numeric, the fields must be of the same data type and contain the same kind of data, but they do not have to have the same name. |
|
compare |
Any relational comparison operator: "=," "<," ">," "<=," ">=," or "<>." |
For more information about inner join syntax, see the topic INNER JOIN Operation.
Show all rows from one table, and corresponding rows from the other table
Outer joins tell a query that although some of the rows on both sides of the join correspond exactly, the query should include all of the rows from one table, and also those rows from the other table that share a common value on both sides of the join.
Outer joins can be left outer joins or can be right outer joins. In a left outer join, the query includes all of the rows from the first table in the SQL statement FROM clause, and only those rows from the other table where the joining field contains values common to both tables. In a right outer join, the query includes all of the rows from the second table in the SQL statement FROM clause, and only those rows from the other table where the joining field contains values common to both tables.
Note: You can easily tell which table is the left table or the right table in a given join by double-clicking the join and then looking in the Join Properties dialog box. You can also switch to SQL view, and then examine the FROM clause.
Because some of the rows on one side of an outer join will not have corresponding rows from the other table, some of the fields returned in the query results from that other table will be empty when the rows do not correspond.
How do I use an outer join?
You create an outer join by modifying an existing inner join. If no inner join exists, you create one, and then change it to an outer join.
Change an inner join to an outer join
-
In query Design view, double-click the join you want to change.
The Join Properties dialog box appears.
-
In the Join Properties dialog box, note the choices listed beside option 2 and option 3.
-
Click the option that you want to use, and then click OK.
-
Access displays the join and shows an arrow that points from the data source where all rows will be included to the data source where only those rows that satisfy the join condition will be included.
Ambiguous outer joins
If you create a query that contains a LEFT JOIN and an INNER JOIN, Access may not be able to determine which join operation to perform first. Because the results are different depending on whether the left join or the inner join is performed first, Access displays an error message:
To correct this error, you must modify the query so that it is clear which join to perform first.
SQL syntax for an outer join
Outer joins are specified in SQL in the FROM clause, as shown below:
FROM table1 [ LEFT | RIGHT ] JOIN table2ON table1.field1 compare table2.field2
The LEFT JOIN and RIGHT JOIN operations have these parts:
|
Part |
Description |
|
table1, table2 |
The names of the tables from which records are combined. |
|
field1, field2 |
The names of the fields that are joined. The fields must be of the same data type and contain the same kind of data, but they do not need to have the same name. |
|
compare |
Any relational comparison operator: "=," "<," ">," "<=," ">=," or "<>." |
For more information about outer join syntax, see the topic LEFT JOIN, RIGHT JOIN Operations.
Show all rows from both tables, and join them where a common value exists
When you want to show all rows from two tables and join them based on common values, you use a full outer join. Access does not explicitly support full outer joins, but you can achieve the same effect by using a union query. The following procedure explains how to do this, but if you want more information about union queries, see the See Also section.
To use a union query to perform a full outer join:
-
Create a query that has a left outer join on the field that you want use for a full outer join.
-
On the Home tab, in the Views group, click View, and then click SQL View.
-
Press CTRL+C to copy the SQL code.
-
Delete the semicolon at the end of the FROM clause, and then press ENTER.
-
Type UNION, and then press ENTER.
Note: Do not use the ALL keyword when you use a union query to perform a full outer join.
-
Press CTRL+V to paste the SQL code that you copied in step 3.
-
In the code that you pasted, change LEFT JOIN to RIGHT JOIN.
-
Delete the semicolon at the end of the second FROM clause, and then press ENTER.
-
Add a WHERE clause that specifies that the value of the join field is NULL in the first table listed in the FROM clause (the left table).
For example, if the FROM clause is:
FROM Products RIGHT JOIN [Order Details] ON Products.ID = [Order Details].[Product ID]
You would add the following WHERE clause:
WHERE Products.ID IS NULL
-
Type a semicolon (;) at the end of the WHERE clause to indicate the end of the union query.
-
On the Design tab, in the Results group, click Run.
Cross joins
Cross joins are different from inner and outer joins in that they are not explicitly represented in Access. In a cross join, each row from one table is combined with each row from another table, resulting in what is called a cross product or a Cartesian product. Any time you run a query that has tables that are not explicitly joined, a cross product is the result. Cross joins are usually unintentional, but there are cases where they can be useful.
Why would I use a cross join?
If you want to examine every possible combination of rows between two tables or queries, use a cross join. For example, suppose your business has had a spectacular year, and you are considering giving rebates to your customers. You can build a query that sums each customer's purchases, create a small table that has several possible rebate percentages, and combine the two in another query that performs a cross join. You end up with a query that displays a set of hypothetical rebates for each customer.
How do I use a cross join?
A cross join is produced any time you include tables or queries in your query and do not create at least one explicit join for each table or query. Access combines every row from each table or query that is not explicitly joined to any other table or query to every other row in the results. Consider the rebate scenario from the preceding paragraph. Assume you have 91 customers, and that you want to look at five possible rebate percentages. Your cross join produces 455 rows (the product of 91 and 5).
As you might imagine, unintentional cross joins can create huge numbers of rows in your query results. Moreover, these results are generally meaningless, because if you don't actually intend to combine every row with every other row, most of the combined rows that appear in the results will not make sense. Finally, queries that use unintentional cross joins can take a very long time to run.
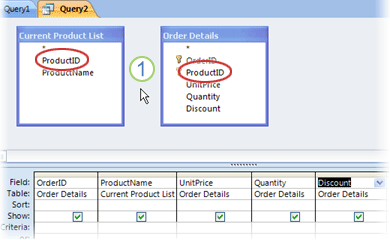
1. The circled fields should be joined to each other.

1. Note the very large number of records.

1. Note that the number of records is much smaller.
Join tables based on an inequality of field values
Joins do not have to be based on the equivalence of the joined fields. A join can be based on any comparison operator, such as greater than (>), less than (<), or does not equal (<>). Joins that are not based on equivalence are called unequal joins.
If you want to combine the rows of two sources of data based on field values that are not equal, you use an unequal join. Typically, unequal joins are based on either the greater than (>), less than (<), greater than or equal to (>=), or less than or equal to (<=) comparison operators. Unequal joins that are based on the does not equal (<>) operator can return almost as many rows as cross joins, and the results can be difficult to interpret.
How do I use an unequal join?
Unequal joins are not supported in Design view. If you wish to use them, you must do so by using SQL view. However, you can create a join in Design view, switch to SQL view, find the equals (=) comparison operator, and change it to the operator you want to use. After you do this, you can only open the query in Design view again if you first change the comparison operator back to equals (=) in SQL view.
Delete a join
If Access automatically creates a join that you do not want, or if you create a join by mistake — for example, a join between two fields that have dissimilar data types — you can delete the join.
-
In the query design grid, click the join you want to remove.
-
Press DELETE.
-or-
-
In the query design grid, right-click the join you want to remove, and then click Delete.