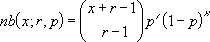Returns the negative binomial distribution. NEGBINOMDIST returns the probability that there will be number_f failures before the number_s-th success, when the constant probability of a success is probability_s. This function is similar to the binomial distribution, except that the number of successes is fixed, and the number of trials is variable. Like the binomial, trials are assumed to be independent.
For example, you need to find 10 people with excellent reflexes, and you know the probability that a candidate has these qualifications is 0.3. NEGBINOMDIST calculates the probability that you will interview a certain number of unqualified candidates before finding all 10 qualified candidates.
Syntax
NEGBINOMDIST(number_f,number_s,probability_s)
Number_f is the number of failures.
Number_s is the threshold number of successes.
Probability_s is the probability of a success.
Remarks
-
Number_f and number_s should be >= 0.
-
Number_f and number_s are truncated to integers.
-
If any argument is nonnumeric, NEGBINOMDIST returns the #VALUE! error value.
-
If probability_s < 0 or if probability > 1, NEGBINOMDIST returns the #NUM! error value.
-
The equation for the negative binomial distribution is:
where:
x is number_f, r is number_s, and p is probability_s.
Example
|
Number_f |
Number_s |
Probability_s |
Formula |
Description (Result) |
|
10 |
5 |
0.25 |
=NEGBINOMDIST([Number_f], [Number_s], [Probability_s]) |
Negative binomial distribution for the specified arguments (0.055049) |