Önemli: Office 2016 ve Office 2019 desteği 14 Ekim 2025 tarihinde sona erdi. Her yerde, her cihazdan çalışmak ve destek almaya devam etmek için Microsoft 365’e yükseltin. Microsoft 365’i edinin
Bu makalede, en uygun ürün karışımını belirlemek için durum analizi için kullanabileceğiniz bir Microsoft Excel eklenti programı olan Çözücü'nün kullanımı ele alınmaktadır.
Kârlılığı en üst düzeye çıkaran aylık ürün karışımını nasıl belirleyebilirim?
Şirketlerin genellikle aylık olarak üretecekleri her ürünün miktarını belirlemesi gerekir. En basit haliyle , ürün karışımı sorunu, kârı en üst düzeye çıkarmak için bir ay boyunca üretilmesi gereken her ürünün miktarının nasıl belirleneceğini içerir. Ürün karışımı genellikle aşağıdaki kısıtlamalara uymalıdır:
-
Ürün karışımı kullanılabilir kaynaklardan daha fazla kaynak kullanamaz.
-
Her ürün için sınırlı bir talep vardır. Bir ay boyunca talebin gerektirdiğinden daha fazla ürün üretemiyoruz, çünkü fazla üretim boşa harcanıyor (örneğin, bozulabilir bir ilaç).
Şimdi ürün karışımı sorununun aşağıdaki örneğini çözelim. Bu sorunun çözümünü Şekil 27-1'de gösterilen dosya Prodmix.xlsx bulabilirsiniz.
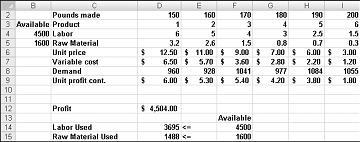
Tesisinde altı farklı ürün üreten bir uyuşturucu şirketinde çalıştığımızı düşünelim. Her ürünün üretimi için işçilik ve hammadde gerekir. Şekil 27-1'deki 4. satır, her ürünün poundunu üretmek için gereken işçilik saatlerini, 5. satırda ise her ürünün poundunu üretmek için gereken hammaddenin libresi gösterilir. Örneğin, bir pound Product 1 üretmek için altı saat işçilik ve 3,2 pound ham madde gerekir. Her ilaç için, pound başına fiyat 6. satırda, pound başına birim maliyet 7. satırda ve pound başına kar katkısı 9. satırda verilir. Örneğin Ürün 2, pound başına 11,00 ABD doları karşılığında satışta bulunur, pound başına 5,70 ABD doları birim maliyetine neden olur ve pound başına 5,30 ABD doları kar sağlar. Her ilaç için ayın talebi 8. satırda verilir. Örneğin, Ürün 3 için talep 1041 pound'dır. Bu ay 4500 saatlik işçilik ve 1600 pound ham madde mevcuttur. Bu şirket aylık kârını nasıl en üst düzeye çıkarabilir?
Excel Çözücü hakkında hiçbir şey bilmiyor olsaydık, ürün karışımıyla ilişkili kar ve kaynak kullanımını izlemek için bir çalışma sayfası oluşturarak bu soruna saldırırdık. Daha sonra, mevcut olandan daha fazla işçilik veya ham madde kullanmadan ve talebin üzerinde herhangi bir ilaç üretmeden kârı iyileştirmek için ürün karışımını değiştirmek için deneme ve hata kullanırız. Çözücü'yü bu işlemde yalnızca deneme ve hata aşamasında kullanırız. Temelde Çözücü, deneme ve hata aramasını kusursuz bir şekilde gerçekleştiren bir iyileştirme altyapısıdır.
Ürün karışımı sorununu çözmenin bir anahtarı, belirli bir ürün karışımıyla ilişkili kaynak kullanımını ve kârı verimli bir şekilde hesaplamaktır. Bu hesaplamayı yapmak için kullanabileceğimiz önemli bir araç TOPLA.ÇARPIM işlevidir. TOPLA.ÇARPIM işlevi hücre aralıklarındaki karşılık gelen değerleri çarpar ve bu değerlerin toplamını döndürür. bir TOPLA.ÇARPIM değerlendirmesinde kullanılan her hücre aralığı aynı boyutlara sahip olmalıdır; bu da TOPLA.ÇARPIM iki satır veya iki sütunla kullanabileceğinizi ancak bir sütun ve bir satırla kullanamayabileceğinizi gösterir.
Ürün karışımı örneğimizde TOPLA.ÇARPIM işlevini nasıl kullanabileceğimize bir örnek olarak kaynak kullanımımızı hesaplamayı deneyelim. İşgücü kullanımımız şu şekilde hesaplanır:
(İlaç 1 pound başına kullanılan işçilik)*(İlaç 1 libre üretildi)+ (İlaç 2 pound başına kullanılan işçilik)*(Üretilen ilaç 2 pound) + ... (İlaç 6'nın poundu başına kullanılan işçilik)*(İlaç 6 libre üretildi)
İşgücü kullanımını D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 olarak daha yorucu bir şekilde hesaplayabiliriz. Benzer şekilde ham madde kullanımı da D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5 olarak hesaplanabilir. Ancak, çalışma sayfasına altı ürün için bu formüllerin girilmesi zaman alır. Örneğin, tesisinde 50 ürün üreten bir şirketle çalışıyorsanız ne kadar süreceğini düşünün. İşgücü ve ham madde kullanımını hesaplamanın çok daha kolay bir yolu, formül TOPLA.ÇARPIM($D$2:$I$2,D4:I4) formülünü D14'ten D15'e kopyalamaktır. Bu formül D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (işçi kullanımımızdır) hesaplar ancak girmek çok daha kolaydır! D2:I2 aralığıyla $ işaretini kullandığıma dikkat edin, böylece formülü kopyalarken 2. satırdaki ürün karışımını yakalamaya devam ediyorum. D15 hücresindeki formül, ham madde kullanımını hesaplar.
Benzer şekilde, kârımız
(Pound başına ilaç 1 kar)*(Üretilen ilaç 1 pound) + (Pound başına ilaç 2 kar)*(Üretilen ilaç 2 pound) + ... (İlaç 6 pound başına kar)*(İlaç 6 pound üretilen)
Kar, D12 hücresinde TOPLA.ÇARPIM(D9:I9,$D$2:$I$2) formülüyle kolayca hesaplanır.
Artık ürün karışımı Çözücü modelimizin üç bileşenini tanımlayabiliriz.
-
Hedef hücre. Hedefimiz kârı en üst düzeye çıkarmaktır (D12 hücresinde hesaplanır).
-
Hücreleri değiştirme. Her ürünün üretilen pound sayısı (D2:I2 hücre aralığında listelenir)
-
Kısıtlama -ları. Aşağıdaki kısıtlamalara sahibiz:
-
Mevcut olandan daha fazla işçilik veya hammadde kullanmayın. Yani, D14:D15 hücrelerindeki değerler (kullanılan kaynaklar), F14:F15 hücrelerindeki değerlerden (kullanılabilir kaynaklar) küçük veya buna eşit olmalıdır.
-
Talepten daha fazla ilaç üretmeyin. Yani, D2:I2 hücrelerindeki değerler (her bir ilaçtan üretilen pound) her bir ilacın talebine eşit veya daha az olmalıdır (D8:I8 hücrelerinde listelenmiştir).
-
Negatif miktarda ilaç üretemiyoruz.
-
Size hedef hücreyi girme, hücreleri değiştirme ve kısıtlamaları Çözücü'ye dönüştürmeyi göstereceğim. Ardından tek yapmanız gereken, kârı en üst düzeye çıkaran ürün karışımını bulmak için Çöz düğmesine tıklamaktır!
Başlamak için Veri sekmesine tıklayın ve Çözümleme grubunda Çözücü'ye tıklayın.
Not: "Excel Çözücü ile İyileştirmeye Giriş" başlıklı 26. Bölümde açıklandığı gibi Çözücü, Microsoft Office Düğmesi'ne, ardından Excel Seçenekleri'ne ve ardından Eklentiler'e tıklanarak yüklenir. Yönet listesinde Excel Eklentileri'ne tıklayın, Çözücü Eklentisi kutusunu işaretleyin ve ardından Tamam'a tıklayın.
Şekil 27-2'de gösterildiği gibi Çözücü Parametreleri iletişim kutusu görüntülenir.
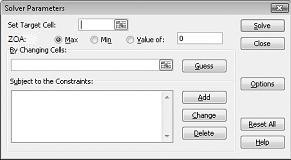
Hedef Hücreyi Ayarla kutusuna tıklayın ve ardından kar hücremizi (D12 hücresi) seçin. Hücreleri Değiştirerek kutusuna tıklayın ve ardından her bir ilacın libresini içeren D2:I2 aralığının üzerine gelin. İletişim kutusu artık Şekil 27-3'e bakmalıdır.
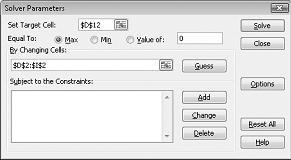
Artık modele kısıtlamalar eklemeye hazırız. Ekle düğmesine tıklayın. Şekil 27-4'te gösterilen Kısıtlama Ekle iletişim kutusunu görürsünüz.
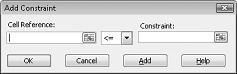
Kaynak kullanımı kısıtlamalarını eklemek için Hücre Başvurusu kutusuna tıklayın ve ardından D14:D15 aralığını seçin. Ortadaki listeden <= öğesini seçin. Kısıtlama kutusuna tıklayın ve F14:F15 hücre aralığını seçin. Kısıtlama Ekle iletişim kutusu artık Şekil 27-5 gibi görünmelidir.
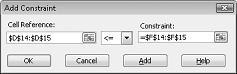
Çözücü değişen hücreler için farklı değerler denediğinde, yalnızca D14<=F14 (kullanılan işçilik kullanılabilir işçilik değerinden küçük veya buna eşittir) ve D15<=F15 (kullanılan ham madde kullanılabilir ham maddeden küçük veya buna eşit) birleşimlerinin dikkate alınacağını garanti ettik. Talep kısıtlamalarını girmek için Ekle'ye tıklayın. Şekil 27-6'da gösterildiği gibi Kısıtlama Ekle iletişim kutusunu doldurun.
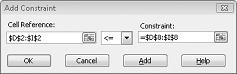
Bu kısıtlamaların eklenmesi, Çözücü değişen hücre değerleri için farklı birleşimler denediğinde yalnızca aşağıdaki parametreleri karşılayan birleşimlerin dikkate alınmasını sağlar:
-
D2<=D8 (İlaç 1'in ürettiği miktar, İlaç 1'e olan talebe eşit veya daha azdır)
-
E2<=E8 (İlaç 2'nin üretilen miktarı, İlaç 2 talebine eşit veya daha azdır)
-
F2<=F8 (Yapılan İlaç 3'ün üretilen miktarı, İlaç 3 talebine eşit veya daha azdır)
-
G2<=G8 (İlaç 4'ün üretilen miktarı, İlaç 4'e olan talebe eşit veya daha azdır)
-
H2<=H8 (İlaç 5'in üretilen miktarı, İlaç 5'e olan talebe eşit veya daha azdır)
-
I2<=I8 (İlaç 6'nın üretilen miktarı, İlaç 6'ya olan talebe eşit veya daha azdır)
Kısıtlama Ekle iletişim kutusunda Tamam'a tıklayın. Çözücü penceresi Şekil 27-7 gibi görünmelidir.
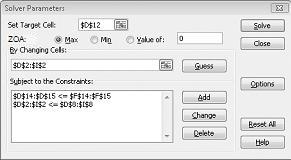
Çözücü Seçenekleri iletişim kutusuna değişen hücrelerin negatif olmamalıdır kısıtlamasını gireriz. Çözücü Parametreleri iletişim kutusunda Seçenekler düğmesine tıklayın. Sonraki sayfada Şekil 27-8'de gösterildiği gibi Doğrusal Modeli Varsay kutusunu ve Negatif Olmadığını Varsay kutusunu işaretleyin. Tamam'a tıklayın.
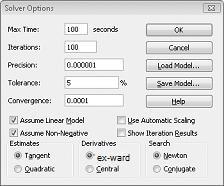
Negatif Olmayan Varsay kutusunun işaretlenmesi, Çözücü'nün yalnızca değişen her hücrenin negatif olmayan bir değer varsaydığı değişen hücrelerin birleşimlerini dikkate almalarını sağlar. Ürün karışımı sorunu doğrusal model olarak adlandırılan özel bir Çözücü sorunu türü olduğundan Doğrusal Modeli Varsay kutusunu işaretledik. Temel olarak, çözücü modeli aşağıdaki koşullar altında doğrusaldır:
-
Hedef hücre, formun terimleri bir araya getirilerek hesaplanır (değişen hücre)*(sabit).
-
Her kısıtlama "doğrusal model gereksinimini" karşılar. Bu, her kısıtlamanın formun terimleri bir araya getirilerek (hücre değiştirilerek)*(sabit) ve toplamları bir sabitle karşılaştırılarak değerlendirildiğini gösterir.
Bu Çözücü sorunu neden doğrusal? Hedef hücremiz (kar) olarak hesaplanır
(Pound başına ilaç 1 kar)*(Üretilen ilaç 1 pound) + (Pound başına ilaç 2 kar)*(Üretilen ilaç 2 pound) + ... (İlaç 6 pound başına kar)*(İlaç 6 pound üretilen)
Bu hesaplama, form terimlerini bir araya getirerek hedef hücrenin değerinin türetildiği bir desen izler (değişen hücre)*(sabit).
İşgücü kısıtlamamız, (İlaç 1'in poundu başına kullanılan emek)*(Üretilen ilaç 1 libre) + (İlaç 2'nin poundu başına kullanılan işçilik)*(Üretilen ilaç 2 libre)+ ... (Bize emek verinİlaç 6)*(Üretilen ilaç 6 pound) başına kullanılabilir işçilik için ed.
Bu nedenle, işçilik kısıtlaması formun terimleri bir araya getirilerek (hücre değiştirilerek)*(sabit) değerlendirilir ve toplamlar bir sabitle karşılaştırılır. Hem işçilik kısıtlaması hem de ham madde kısıtlaması doğrusal model gereksinimini karşılar.
Talep kısıtlamalarımız formu alır
(İlaç 1 üretildi)<=(İlaç 1 Talep) (İlaç 2 üretildi)<=(İlaç 2 Talep) §(Üretilen ilaç 6)<=(İlaç 6 Talep)
Her talep kısıtlaması doğrusal model gereksinimini de karşılar çünkü her biri formun terimleri (değişen hücre)*(sabit) bir araya getirilerek ve toplamlar bir sabitle karşılaştırılarak değerlendirilir.
Ürün karışımı modelimizin doğrusal bir model olduğunu gösterdikten sonra neden önem vemeliyiz?
-
Çözücü modeli doğrusalsa ve Doğrusal Modeli Varsay'ı seçersek Çözücü'nün Çözücü modeline en uygun çözümü bulması garanti edilir. Çözücü modeli doğrusal değilse Çözücü en uygun çözümü bulabilir veya bulamayabilir.
-
Çözücü modeli doğrusalsa ve Doğrusal Modeli Varsay'ı seçersek Çözücü, modelin en uygun çözümünü bulmak için çok verimli bir algoritma (simplex yöntemi) kullanır. Çözücü modeli doğrusalsa ve Doğrusal Modeli Varsay'ı seçmiyorsak, Çözücü çok verimsiz bir algoritma (GRG2 yöntemi) kullanır ve modelin en uygun çözümünü bulmakta zorlanabilir.
Çözücü Seçenekleri iletişim kutusunda Tamam'a tıkladıktan sonra, şekil 27-7'de daha önce gösterilen ana Çözücü iletişim kutusuna döneriz. Çöz'e tıkladığımızda Çözücü, ürün karışımı modelimiz için en uygun çözümü (varsa) hesaplar. 26. Bölümde belirttiğim gibi, ürün karışımı modeline en uygun çözüm, tüm uygulanabilir çözümler kümesi üzerinde kârı en üst düzeye çıkaran bir dizi değişen hücre değeri (her bir ilacın libresi) olacaktır. Yine uygulanabilir bir çözüm, tüm kısıtlamaları karşılayan değişen hücre değerleri kümesidir. Şekil 27-9'da gösterilen değişen hücre değerleri uygulanabilir bir çözümdür çünkü tüm üretim düzeyleri negatif değildir, üretim düzeyleri talebi aşmaz ve kaynak kullanımı kullanılabilir kaynakları aşmaz.
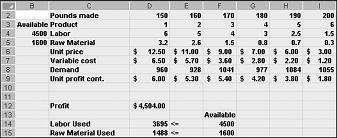
Sonraki sayfada Şekil 27-10'da gösterilen değişen hücre değerleri, aşağıdaki nedenlerle uygulanabilir bir çözümü temsil eder:
-
İlaç 5'in talepten daha fazlasını üretiyoruz.
-
Mevcut olandan daha fazla iş gücü kullanırız.
-
Mevcut olandan daha fazla ham madde kullanıyoruz.
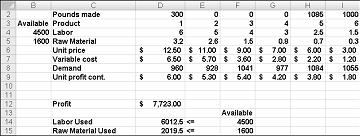
Çöz'e tıkladıktan sonra Çözücü, Şekil 27-11'de gösterilen en uygun çözümü hızla bulur. Çalışma sayfasındaki en uygun çözüm değerlerini korumak için Çözücü Çözümünü Koru'ya seçmeniz gerekir.
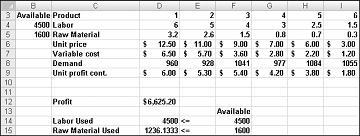
İlaç şirketimiz, 596.67 pound İlaç 4, 1084 pound İlaç 5 üreterek aylık kârını 6,625.20 $ seviyesinde en üst düzeye çıkarabilir ve diğer ilaçların hiçbiri! 6.625,20 ABD doları tutarındaki maksimum kârı başka şekillerde elde edebilir miyiz, karara varamayız. Emin olabileceğimiz tek şey, sınırlı kaynak ve talebimizle bu ay 6.627.20 ABD dolarından fazlasını yapma imkanının olmadığıdır.
Her ürün için talebin karşılanması gerektiğini varsayalım. (Dosya Prodmix.xlsx Uygun Çözüm Yok çalışma sayfasına bakın.) Ardından talep kısıtlamalarımızı D2:I2<=D8:I8 yerine D2:I2>=D8:I8 olarak değiştirmeliyiz. Bunu yapmak için Çözücü'yü açın, D2:I2<=D8:I8 kısıtlamasını seçin ve değiştir'e tıklayın. Şekil 27-12'de gösterilen Kısıtlamayı Değiştir iletişim kutusu görüntülenir.
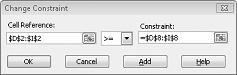
>= öğesini seçin ve ardından Tamam'a tıklayın. Artık Çözücü'nün yalnızca tüm talepleri karşılayan hücre değerlerini değiştirmeyi düşüneceğini garanti ettik. Çöz'e tıkladığınızda "Çözücü uygun bir çözüm bulamadı" iletisini görürsünüz. Bu ileti, modelimizde hata yaptığımız anlamına gelmez, ancak sınırlı kaynaklarımızla tüm ürünler için talebi karşılayamayız. Çözücü, her ürün için talebi karşılamak istiyorsak daha fazla iş gücü, daha fazla ham madde veya her ikisini birden eklememiz gerektiğini söylüyor.
Her ürün için sınırsız talebe izin verirsek ve her bir ilacın negatif miktarlarının üretilmesine izin verirsek ne olacağını görelim. (Bu Çözücü sorununu dosya Prodmix.xlsx Değerleri Ayarlama Yakınsanma çalışma sayfasında görebilirsiniz.) Bu duruma en uygun çözümü bulmak için Çözücü'yü açın, Seçenekler düğmesine tıklayın ve Negatif Olmayan Varsay kutusunu temizleyin. Çözücü Parametreleri iletişim kutusunda, talep kısıtlaması D2:I2<=D8:I8'i seçin ve ardından kısıtlamayı kaldırmak için Sil'e tıklayın. Çöz'e tıkladığınızda, Çözücü "Hücre Değerlerini Ayarlama Yakınsanmasın" iletisini döndürür. Bu ileti, hedef hücre en üst düzeye çıkarılacaksa (örneğimizde olduğu gibi), rastgele olarak büyük hedef hücre değerlerine sahip uygulanabilir çözümler olduğu anlamına gelir. (Hedef hücre simge durumuna küçültülecekse, "Hücre Değerlerini Ayarlama Yakınsanmasın" iletisi, rastgele küçük hedef hücre değerlerine sahip uygulanabilir çözümler olduğu anlamına gelir.) Bizim durumumuzda, bir ilacın negatif üretimine izin vererek, rastgele olarak büyük miktarlarda başka ilaçlar üretmek için kullanılabilecek "kaynak" oluştururuz. Sınırsız talebimiz göz önüne alındığında, bu sınırsız kar elde etmemize olanak tanır. Gerçek bir durumda, sonsuz miktarda para kazanamayız. Kısacası, "Değerleri Ayarlama Yakınsanma" ifadesini görürseniz modelinizde bir hata vardır.
-
İlaç şirketimizin, geçerli işçilik maliyetlerinden 1 $ daha fazla saatte 500 saate kadar iş gücü satın alabildiğini varsayalım. Kârı nasıl en üst düzeye çıkarabiliriz?
-
Bir yonga üretim tesisinde, dört teknisyen (A, B, C ve D) üç ürün üretir (Ürünler 1, 2 ve 3). Bu ay, yonga üreticisi 80 adet Ürün 1, 50 adet Ürün 2 ve en fazla 50 adet Ürün 3 satabilir. Teknisyen A sadece Ürünler 1 ve 3 yapabilir. Teknisyen B sadece Ürünler 1 ve 2 yapabilir. Teknisyen C sadece Ürün 3 yapabilir. Teknisyen D sadece Ürün 2 yapabilir. Üretilen her birim için ürünler şu kâra katkıda bulunur: Ürün 1, $6; Ürün 2, $7; ve Ürün 3, $10. Her teknisyenin bir ürün üretmesi gereken süre (saat cinsinden) aşağıdaki gibidir:
Ürün
Teknisyen A
Teknisyen B
Teknisyen C
Teknisyen D
1
2
2,5
Yapılamaz
Yapılamaz
2
Yapılamaz
3
Yapılamaz
3,5
3
3
Yapılamaz
4
Yapılamaz
-
Her teknisyen ayda 120 saate kadar çalışabilir. Yonga üreticisi aylık kârını nasıl en üst düzeye çıkarabilir? Kesirli birim sayısının üretilebileceğini varsayalım.
-
Bir bilgisayar üretim tesisi fareler, klavyeler ve video oyunu oyun çubukları üretir. Birim başına kar, birim başına iş gücü kullanımı, aylık talep ve birim başına makine zamanı kullanımı aşağıdaki tabloda verilmiştir:
Fareler
Klavyeler
Joystick
Kar/birim
8 ABD doları
11 ABD doları
9 ABD doları
İşgücü kullanımı/birimi
0,2 saat
0,3 saat
0,24 saat
Makine zamanı/birimi
.04 saat
0,055 saat
.04 saat
Aylık talep
15.000
27,000
11,000
-
Her ay toplam 13.000 iş saati ve 3000 saat makine süresi mevcuttur. Üretici, fabrikanın aylık kar katkısını nasıl en üst düzeye çıkarabilir?
-
Her ilaç için en az 200 birim talebin karşılanması gerektiğini varsayarak ilaç örneğimizi çözün.
-
Jason elmas bilezikler, kolyeler ve küpeler yapar. Ayda en fazla 160 saat çalışmak istiyor. 800 ons elması var. Her ürünü üretmek için gereken kar, işçilik süresi ve elmasların onsları aşağıda verilmiştir. Her ürün için talep sınırsızsa, Jason kârını nasıl en üst düzeye çıkarabilir?
Ürün
Birim kar
Birim başına çalışma saatleri
Birim başına ons elmas
Bilezik
300 TL
.35
1.2
Kolye
200 TL
.15
.75
Küpe
100 TL
0,05
.5










