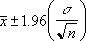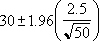Normal dağılıma sahip bir popülasyon ortalaması için güvenilirlik aralığını döndürür. Güvenilirlik aralığı, örnek ortalamanın her iki tarafındaki aralıktır. Örneğin, bir ürünü posta yoluyla sipariş ederseniz, belirli bir güven düzeyiyle ürünün en erken ve en son ulaşacağını belirleyebilirsiniz.
Söz dizimi
GÜVENİlİRLİk(alfa,standard_dev,boyut)
Alfa güvenilirlik düzeyini hesaplamak için kullanılan anlam düzeyidir. Güvenirlik düzeyi, %100*(1 - alfa)'ya eşittir; veya başka bir deyişle 0,05 düzeyindeki bir alfa, yüzde 95 güvenirlik düzeyi belirtir.
Standart_sapma veri aralığının popülasyon standart sapmasıdır ve bilindiği varsayılır.
Boyut örnek boyutudur.
Açıklamalar
-
Bağımsız değişken sayısal değilse GÜVENİlİRLİk işlevi #VALUE! hata değeri verir.
-
Alfa ≤ 0 veya alfa ≥ 1 ise GÜVENİlİRLİk, #NUM verir! hata değeri verir.
-
standard_dev ≤ 0 ise GÜVENİlİRLİk işlevi #NUM! hata değerini verir.
-
Boyut, tamsayı değilse, fazlalıkları atılır.
-
Boyut 1< ise GÜVENİlİRLİk işlevi #NUM! hata değerini verir.
-
Alfanın 0,05'e eşit olduğunu varsayarsak, standart normal eğrinin altındaki (1 - alfa)ya veya yüzde 95'e eşit olan alanı hesaplamamız gerekir. Bu değer, ± 1,96'dır. Öyleyse, GÜVENİRLİK aralığı:
Örnek
50 yolcu örneğimizde ortalama işe seyahat uzunluğunun 30 dakika olduğunu ve popülasyon standart sapması 2,5 olduğunu gözlemlediğimizi varsayalım. Popülasyon ortalamasının aralıkta olduğundan yüzde 95 emin olabilirsiniz:
|
Alfa |
StdDev |
Boyut |
Formül |
Açıklama (Sonuç) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=GÜVENİlİRLİk([Alfa],[StdDev],[Boyut]) |
Bir popülasyon ortalaması için güvenirlik aralığı. Başka bir deyişle, işe seyahatin ortalama uzunluğu 30 ± 0,692951 dakika veya 29,3 ile 30,7 dakika arasındadır. (0.692951) |