Renvoie la probabilité d’une variable aléatoire discrète suivant la loi binomiale. Utilisez la fonction LOI.BINOMIALE pour résoudre des problèmes comportant un nombre de tests ou d’essais déterminé, lorsque le résultat des essais ne peut être qu’un succès ou un échec, lorsque les essais sont indépendants ou lorsque la probabilité de succès est constante au cours des expérimentations. La fonction LOI.BINOMIALE peut, par exemple, calculer la probabilité pour que deux des trois enfants à naître soient des garçons.
Important : Cette fonction a été remplacée par une ou plusieurs nouvelles fonctions proposant une meilleure précision et dont les noms reflètent mieux leur rôle. Bien que cette fonction soit toujours disponible à des fins de compatibilité descendante, nous vous conseillons d’utiliser les nouvelles fonctions dès maintenant, car cette fonction risque de ne plus être disponible dans les versions ultérieures d’Excel.
Pour plus d’informations sur la nouvelle fonction, voir fonction LOI.BINOMIALE.N.
Syntaxe
LOI.BINOMIALE(nombre_s,essais,probabilité_s,cumulative)
La syntaxe de la fonction LOI.BINOMIALE contient les arguments suivants :
-
nombre_s Obligatoire. Représente le nombre d’essais réussis.
-
essais Obligatoire. Représente le nombre d’essais indépendants.
-
probabilité_s Obligatoire. Représente la probabilité de succès de chaque essai.
-
cumulative Obligatoire. Représente une valeur logique qui détermine le mode de calcul de la fonction. Si l’argument cumulative a la valeur VRAI, alors LOI.BINOMIALE renvoie la fonction de distribution cumulée qui représente la probabilité qu’il y ait au plus nombre_s succès ; si l’argument cumulative a la valeur FAUX, LOI.BINOMIALE renvoie la fonction de probabilité de masse qui représente la probabilité qu’il y ait nombre_s succès.
Remarques
-
Les arguments nombre_s et essais sont tronqués à leur partie entière.
-
Si number_s, essais ou probability_s n’est pas numérique, BINOMDIST renvoie la #VALUE ! renvoie la valeur d’erreur.
-
Si number_s < 0 ou number_s > essais, BINOMDIST renvoie le #NUM ! renvoie la valeur d’erreur.
-
Si probability_s < 0 ou probability_s > 1, BINOMDIST renvoie la #NUM ! renvoie la valeur d’erreur.
-
Si x = nombre_s, n = essais, et p = probabilité_s, la fonction de masse de probabilité binomiale est :
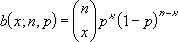
où :

est COMBIN(n,x).
-
Si x = nombre_s, n = essais, et p = probabilité_s, la distribution binomiale cumulative est :
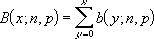
Exemple
Copiez les données d’exemple dans le tableau suivant, et collez-le dans la cellule A1 d’un nouveau classeur Excel. Pour que les formules affichent des résultats, sélectionnez-les, appuyez sur F2, puis sur Entrée. Si nécessaire, vous pouvez modifier la largeur des colonnes pour afficher toutes les données.
|
Données |
Description |
|
|
6 |
Nombre d’essais réussis |
|
|
10 |
Nombre d’essais indépendants |
|
|
0,5 |
Probabilité de succès de chaque essai |
|
|
Formule |
Description |
Résultat |
|
=LOI.BINOMIALE(A2,A3,A4,FAUX) |
Probabilité d’obtenir exactement 6 essais réussis sur 10. |
0,2050781 |










