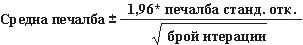Тази статия е адаптирана от анализа на данни на Microsoft Excel и моделирането на бизнеса от Уейн Уинстън.
-
Кой използва симулацията на Монте Карло?
-
Какво се случва, когато въведете =RAND() в клетка?
-
Как можете да симулирате стойности на отделна случайна променлива?
-
Как можете да симулирате стойности на нормална случайна променлива?
-
Как една фирма за поздравителни картички може да определи колко картички да се създадат?
Бихме искали да оценим точно вероятността за несигурни събития. Каква е например вероятността паричните потоци на новия продукт да имат положителна нетна настояща стойност (NPV)? Какъв е рисковият фактор на нашето инвестиционно портфолио? Симулацията на Монте Карло ни дава възможност да моделираме ситуации, които са свързани с несигурност, и след това да ги разиграем хиляди пъти на компютър.
Забележка: Симулацията на име Монте Карло идва от компютърните симулации, извършени през 30-те и 40-те, за да се прецени вероятността верижната реакция, необходима за детонатната бомба да проработи успешно. Физиците, участващи в тази работа, са били големи почитатели на хазарта, така че дадоха симулации кодово име Монте Карло.
В следващите пет глави ще видите примери как можете да използвате Excel за извършване на симулации на Монте Карло.
Много компании използват симулацията "Монте Карло" като важна част от процеса на вземане на решения. Ето някои примери.
-
Симулации на general Motors, Proctor и Gamble, Pfizer, Bristol-Myers Squibb и Eli Lilly за оценка на средната възвръщаемост и рисковия фактор на новите продукти. В ГМО тази информация се използва от изпълнителния директор, за да се определи кои продукти се пускат на пазара.
-
ГМО използва симулация за дейности като прогнозиране на нетния доход за корпорацията, прогнозиране на структурните разходи и разходите за закупуване и определяне на неговата податливост към различни видове риск (като например промени в лихвените курсове и колебания в обменния курс).
-
Lilly използва симулация за определяне на оптималния капацитет на растенията за всяко лекарство.
-
Proctor и Gamble използват симулация за моделиране и оптимално хеджиране на валутния риск.
-
Sears uses simulation to determine how many units of each product line should be ordered from suppliers – например the number of pairs of Dockers trousers that should be ordered this year.
-
Нефтените и нарко-компаниите използват симулация, за да изложат "реални опции", например стойността на опция за разширяване, свиване или отлагане на даден проект.
-
Финансовите планировчи използват симулацията на Монте Карло за определяне на оптимални инвестиционни стратегии за оттеглянето на своите клиенти.
Когато въведете формулата =RAND() в дадена клетка, получавате число, което е също толкова вероятно да приеме всяка стойност между 0 и 1. По този начин, около 25 процента от времето, трябва да получите число по-малко или равно на 0,25; около 10 процента от времето трябва да получите число, което е поне 0,90 и т.н. За да покажете как работи функцията RAND, погледнете файла Randdemo.xlsx, показан на фигура 60–1.
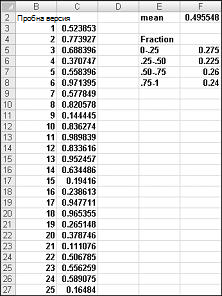
Забележка: Когато отворите файла Randdemo.xlsx, няма да видите същите случайни числа, показани на фигура 60-1. Функцията RAND винаги преизчислява автоматично числата, които генерира при отваряне на работен лист или при въвеждане на нова информация в работния лист.
Първо, копирайте от клетка C3 в C4:C402 формулата =RAND(). След това наименуване на диапазона C3:C402 Data. След това в колона F можете да проследявате средната стойност на 400 случайни числа (клетка F2) и да използвате функцията COUNTIF, за да определите дробите, които са между 0 и 0,25, 0,25 и 0,50, 0,50 и 0,75 и 0,75 и 1. Когато натиснете клавиша F9, случайните числа се преизчисляват. Обърнете внимание, че средната стойност на 400 числа винаги е приблизително 0,5 и че около 25 процента от резултатите са на интервали от 0,25. Тези резултати съответстват на определението за случайно число. Също така обърнете внимание, че стойностите, генерирани от RAND в различни клетки, са независими. Ако например случайното число, генерирано в клетка C3, е голямо число (например 0,99), то не ни казва нищо за стойностите на другите генерирани случайни числа.
Да предположим, че търсенето на календар се управлява от следната отделна случайна променлива:
|
Търсене |
"вероятност" |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Как можем да накараме Excel да изпълни или симулира това търсене на календари много пъти? Номерът е да свържете всяка възможна стойност на функцията RAND с възможно търсене на календари. Следващата задача гарантира, че търсенето на 10 000 ще е 10 процента от времето и т.н.
|
Търсене |
Присвоено случайно число |
|---|---|
|
10 000 |
По-малко от 0,10 |
|
20 000 |
По-голямо или равно на 0,10 и по-малко от 0,45 |
|
40,000 |
По-голямо или равно на 0,45 и по-малко от 0,75 |
|
60 000 |
По-голямо или равно на 0,75 |
За да демонстрирате симулацията на търсенето, погледнете файла Discretesim.xlsx, показан на фигура 60-2 на следващата страница.
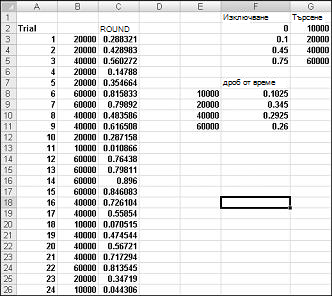
Ключът към нашата симулация е да използваме случайно число, за да инициирате търсене от диапазона на таблицата F2:G5 (наименувано търсене). Случайни числа, по-големи или равни на 0 и по-малки от 0,10, ще доведат до търсене с 10 000; случайни числа, по-големи или равни на 0,10 и по-малки от 0,45, ще доведат до търсене от 20 000; случайни числа, по-големи или равни на 0,45 и по-малки от 0,75, ще доведат до търсене от 40 000; и случайни числа, по-големи или равни на 0,75, ще доведат до търсене на 60 000. Генерирате 400 случайни числа, като копирате от C3 до C4:C402 формулата RAND(). След това генерирате 400 пробни версии или итерации на търсенето в календара, като копирате от B3 в B4:B402 формулата VLOOKUP(C3;справка;2). Тази формула гарантира, че всяко случайно число, по-малко от 0,10, генерира търсене на 10 000, всяко случайно число между 0,10 и 0,45 генерира търсене от 20 000 и т.н. В диапазона от клетки F8:F11 използвайте функцията COUNTIF, за да определите дробта на нашите 400 итерации, породили всяко търсене. Когато натиснете F9, за да преизчислим случайните числа, симулираните вероятности са близо до нашите предполагаеми вероятности за търсене.
Ако въведете в някоя клетка формулата NORMINV(rand();mu,sigma), ще генерирате симулирана стойност на нормална случайна променлива, която има средно mu и сигма на стандартното отклонение. Тази процедура е показана във файла Normalsim.xlsx, показан на фигура 60-3.
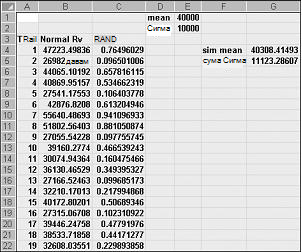
Да предположим, че искаме да симулираме 400 опита или итерации за нормална случайна променлива със средна стойност 40 000 и стандартно отклонение 10 000. (Можете да въведете тези стойности в клетките E1 и E2 и да наименуване съответно на тези клетки със средна стойност и сигма.) Копирането на формулата =RAND() от C4 до C5:C403 генерира 400 различни случайни числа. Копирането от B4 до B5:B403 на формулата NORMINV(C4;средно;сигма) генерира 400 различни стойности на опити от нормална случайна променлива със средна стойност 40 000 и стандартно отклонение 10 000. Когато натиснете клавиша F9, за да преизчислим случайните числа, средната стойност остава близо до 40 000, а стандартното отклонение е близо до 10 000.
По същество за случайно число x формулата NORMINV(p,mu,sigma) генерира p-тияпроцентил на нормална случайна променлива със средно му исигма при стандартно отклонение. Например случайното число 0,77 в клетка C4 (вж. фигура 60-3) генерира в клетка B4 приблизително 77-я процентил на нормална случайна променлива със средна стойност 40 000 и стандартно отклонение 10 000.
В този раздел ще видите как симулацията на Монте Карло може да се използва като инструмент за вземане на решения. Да предположим, че търсенето на картичка за св. Валентин се управлява от следната отделна случайна променлива:
|
Търсене |
"вероятност" |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Поздравителната картичка се продава за 4,00 щ.в., а променливият разход за произвеждане на всяка картичка е 1,50 щ.в. Левите карти трябва да се изхвърлят на стойност от 0,20 щ.в. на карта. Колко картички трябва да се отпечатат?
По принцип симулираме всяко възможно количество в производството (10 000, 20 000, 40 000 или 60 000) много пъти (например 1000 итерации). След това определяме кое количество по поръчка дава максималната средна печалба над 1000 итерации. Можете да намерите данните за този раздел във файловия Valentine.xlsx, показан на фигура 60-4. Можете да присвоите имената на диапазоните в клетки B1:B11 на клетки C1:C11. На диапазона от клетки G3:H6 се присвоява справка за име. Нашите параметри за продажните цени и разходите се въвеждат в клетки C4:C6.
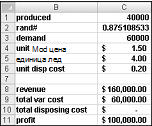
Можете да въведете пробно производствено количество (40 000 в този пример) в клетка C1. След това създайте случайно число в клетка C2 с формулата =RAND(). Както беше описано по-горе, симулирате търсенето на картата в клетка C3 с формулата VLOOKUP(rand,lookup,2). (Във формулата VLOOKUP rand е името на клетката, присвоено на клетка C3, а не на RAND функцията.)
Броят продадени бройки е по-малкият от нашето количество и търсене в производството. В клетка C8 изчислявате нашите приходи с формулата MIN(произведено,търсене)*unit_price. В клетка C9 изчислявате общите производствени разходи с формулата, произведена*unit_prod_cost.
Ако произвеждаме повече карти, отколкото са търсени, броят на единиците, които са останали, е равен на производство минус търсене; в противен случай няма останали единици. Изчисляваме нашите разходи за изхвърляне в клетка C10 с формулата unit_disp_cost*IF(произвежда>търсене, произвеждано – търсене,0). Накрая, в клетка C11 изчисляваме печалбата си като приход – total_var_cost total_disposing_cost.
Бихме искали един ефективен начин да натиснете F9 много пъти (например 1000) за всяко количество продукция и да обобщите очакваната ни печалба за всяко количество. Тази ситуация е такава, в която двупосочна таблица с данни идва на помощ. (Вижте глава 15 "Анализ на чувствителността с таблици с данни" за подробности относно таблиците с данни.) Таблицата с данни, използвана в този пример, е показана на фигура 60–5.
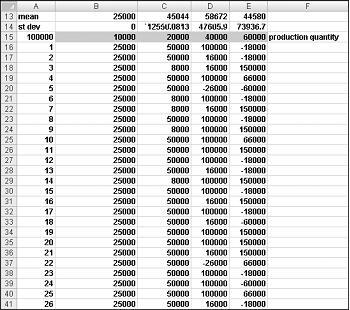
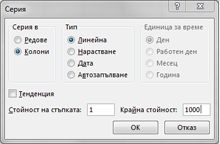
В диапазона от клетки A16:A1015 въведете числата 1 – 1000 (съответстващи на нашите 1000 опита). Един лесен начин да създадете тези стойности е да започнете с въвеждане на 1 в клетка A16. Изберете клетката и след това в раздела Начало , в групата Редактиране щракнете върху Запълване и изберете Серия , за да се покаже диалоговият прозорец Серия . В диалоговия прозорец Серия , показан на Фигура 60-6, въведете Стойност на стъпка 1 и Стойност на стоп от 1000. В областта Серия В изберете опцията Колони и след това щракнете върху OK. Числата 1 –1000 ще бъдат въведени в колона A, започвайки от клетка A16.
След това въвеждаме нашите възможни производствени количества (10 000, 20 000, 40 000, 60 000) в клетки B15:E15. Искаме да изчислим печалбата за всеки пробен номер (от 1 до 1000) и за всяко количество продукция. Препращаме към формулата за печалба (изчислена в клетка C11) в горната лява клетка на нашата таблица с данни (A15), като въвеждаме =C11.
Сега сме готови да трием Excel в симулирането на 1000 итерации на търсенето за всяко производствено количество. Изберете диапазона от таблици (A15:E1014) и след това в групата Инструменти за данни на раздела Данни щракнете върху Условен анализ и след това изберете Таблица с данни. За да настроите двупосочна таблица с данни, изберете нашето производствено количество (клетка C1) като клетка за въвеждане на ред и изберете произволна празна клетка (избрахме клетка I14) като клетка за въвеждане на колона. След като щракнете върху OK, Excel симулира 1000 стойности на търсенето за всяко количество поръчки.
За да разберете защо това работи, помислете за стойностите, поставени от таблицата с данни в диапазона от клетки C16:C1015. За всяка от тези клетки Excel ще използва стойност 20 000 в клетка C1. В C16 стойността на входната клетка на колоната 1 се поставя в празна клетка и случайното число в клетка C2 се преизчислява. Съответната печалба след това се записва в клетка C16. След това входната стойност на клетка от колоната 2 се поставя в празна клетка и случайното число в C2 отново се преизчислява. Съответната печалба се въвежда в клетка C17.
Чрез копиране от клетка B13 в C13:E13 на формулата AVERAGE(B16:B1015) изчисляваме средната симулирана печалба за всяко производствено количество. Чрез копиране от клетка B14 на C14:E14 формулата STDEV(B16:B1015), ние изчисляваме стандартното отклонение на нашите симулирани печалби за всяко количество поръчки. Всеки път, когато натиснете F9, 1000 итерации на търсенето се симулират за всяко количество за поръчка. Създаването на 40 000 карти винаги дава най-голямата очаквана печалба. Следователно изглежда, че създаването на 40 000 карти е правилното решение.
Въздействието на риска върху нашето решение Ако сме произвели 20 000 вместо 40 000 карти, очакваната ни печалба намалява приблизително с 22 процента, но нашият риск (измерен чрез стандартното отклонение на печалбата) намалява почти 73 процента. Следователно, ако сме крайно обратни на риска, създаването на 20 000 карти може да е правилното решение. Между другото, произвеждайки 10 000 карти, винаги има стандартно отклонение от 0 карти, защото ако получим 10 000 карти, ние винаги ще ги продаваме без никакви остатъци.
Забележка: В тази работна книга опцията Изчисляване е зададена на Автоматично с изключение на таблиците. (Използвайте командата Изчисление в групата Изчисление на раздела Формули.) Тази настройка гарантира, че нашата таблица с данни няма да се преизчислява, освен ако не натиснете F9, което е добра идея, тъй като една голяма таблица с данни ще забави работата ви, ако се преизчислява всеки път, когато въвеждате нещо в работния лист. Обърнете внимание, че в този пример, когато натиснете F9, средната печалба ще се промени. Това се случва, защото всеки път, когато натиснете F9, се използва различна последователност от 1000 случайни числа за генериране на искания за всяко количество поръчки.
Доверителен интервал за средна печалба Естествен въпрос, който да се зададе в тази ситуация е, в какъв интервал сме 95 процента сигурни, че истинската средна печалба ще падне? Този интервал се нарича 95 процента доверителен интервал за средната печалба. 95-процентният доверителен интервал за средната стойност на всяка изходна симулация се изчислява по следната формула:
В клетка J11 изчислявате долната граница за 95-процентния доверителен интервал върху средната печалба, когато се произвеждат 40 000 календара с формулата D13 – 1,96*D14/SQRT(1000). В клетка J12 изчислявате горната граница за нашия 95 процента доверителен интервал с формулата D13+1,96*D14/SQRT(1000). Тези изчисления са показани на фигура 60—7.
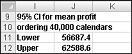
Ние сме 95 процента сигурни, че нашата средна печалба, когато 40,000 календари са подредени е между $56,687 and $62,589.
-
Дилър на GMC смята, че търсенето на пратеници от 2005 г. обикновено ще бъде разпределено със средна стойност 200 и стандартно отклонение от 30. Цената му за получаване на пратеник е 25 000 лв. и продава пратеник за 40 000 лв. Половината от всички Envoys, които не се продават на пълна цена, могат да се продават за 30 000 лв. Обмисля да поръча 200, 220, 240, 260, 280 или 300 Пратеници. Колко трябва да поръча?
-
Малък супермаркет се опитва да определи колко копия на Хора списание трябва да поръчат всяка седмица. Те вярват, че тяхното търсене на Хора се управлява от следната дискретна случайна променлива:
Търсене
"вероятност"
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Супермаркетът плаща $1,00 за всяко копие на Хора и го продава за $1,95. Всяко непродадено копие може да бъде върнато за $0,50. Колко копия на Хора трябва да съхранява поръчката?
Имате нужда от още помощ?
Винаги можете да попитате експерт в техническата общност на Excel или да получите поддръжка в Общността за отговори от.