Забележка: Бихме искали да ви осигурим най-новото помощно съдържание възможно най-бързо на вашия собствен език. Тази страница е преведена чрез автоматизация и може да съдържа граматически грешки и несъответствия. Нашата цел е това съдържание да ви бъде полезно. Можете ли да ни кажете дали информацията е била полезна за вас, в дъното на тази страница? Ето статията на английски за бърза справка.
Тази статия описва използването на Solver – добавка за Microsoft Excel, която можете да използвате за условен анализ, за да определите оптимален продуктов микс.
Как мога да определя месечния продуктов микс, който максимизира рентабилността?
Компаниите често трябва да определят количеството на всеки продукт за производство на месечна база. В най-простия си вид Проблемът със смесването на продукти включва как да се определи размерът на всеки продукт, който трябва да бъде произведен през месец, за да се увеличат печалбите. Миксът от продукти трябва обикновено да се придържа към следните ограничения:
-
Миксът от продукти не може да използва повече ресурси, отколкото са налични.
-
Има ограничено търсене за всеки продукт. Не можем да произвеждаме повече от един продукт през месец, отколкото търсенето диктува, тъй като излишната продукция се губи (например нетраен наркотик).
Нека сега решим следния пример за проблема с микса на продукта. Можете да намерите решението на този проблем във файла Prodmix. xlsx, показан на фигура 27-1.
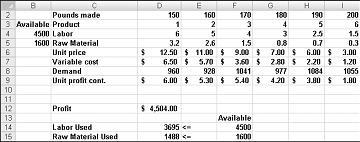
Да речем, че работим за фирма за наркотици, която произвежда шест различни продукта при тяхното растение. Производството на всеки продукт изисква трудови и сурови материали. Ред 4 във фигура 27-1 показва часовете труд, необходими за производството на паунд от всеки продукт, а ред 5 показва паунда на суровината, необходима за производството на паунд от всеки продукт. Например създаването на паунд от продукт 1 изисква шест часа труд и 3,2 паунда на суровината. За всеки наркотик цената за паунд е дадена в ред 6, единичните разходи за паунд се дават в ред 7 и печалбата за паунд е дадена в ред 9. Например продуктите 2 се продават за $11,00 за паунд, което води до разходи за единица на $5,70 за паунд и допринася за печалбата от $5,30 за паунд. Търсенето на месец за всеки наркотик е дадено в ред 8. Например търсенето на продукт 3 е 1041 паунда. Този месец са налични 4500 часа труд и 1600 паунда на суровината. Как тази фирма може да увеличи своята месечна печалба?
Ако не знаем нищо за Solver за Excel, ние ще атакуваме този проблем, като създадем работен лист, за да проследим печалбата и използването на ресурсите, свързани с продуктовия микс. След това ще използваме изпробване и грешка, за да променяме продуктовия микс, за да оптимизираме печалбата, без да използваме повече труд или суровина, отколкото е налична, и без да произвеждаме наркотици повече от търсенето. Ние използваме Solver в този процес само при етап на изпробване и грешка. По същество Solver е двигател за оптимизиране, който безупречно извършва търсенето при опит и грешки.
Ключът към решаването на проблема с продуктовия микс е ефективно да се изчисли използването на ресурсите и печалбата, свързани с даден продукт. Важен инструмент, който можем да използваме, за да направим това изчисление, е функцията SUMPRODUCT. Функцията SUMPRODUCT умножава съответните стойности в диапазони от клетки и връща сумата на тези стойности. Всеки диапазон от клетки, използван в оценка на SUMPRODUCT, трябва да има същите размери, което означава, че можете да използвате SUMPRODUCT с два реда или две колони, но не и с една колона и един ред.
Като пример как можем да използваме функцията SUMPRODUCT в нашия пример за продуктов микс, нека опитаме да изчислим използването на ресурсите си. Нашата работа по труд се изчислява чрез
(Труда се използва за паунд от наркотиците 1) * (наркотици £ 1) + (труда се използва за паунд на наркотици 2) * (наркотици 2 паунда) +.. . (Труда се използва за паунд от наркотиците 6) * (наркотици 6 паунда)
Бихме могли да изчислим използването на работната ръка по по-досаден начин като D2 * D4 + Е2 * E4 + F2 * F4 + G2 * G4 + Н2 * H4 + I2 * i4. По подобен начин употребата на сурови материали може да бъде изчислена като D2 * D5 + Е2 *E5 + F2 * F5 + G2 * G5 + Н2 * H5 + I2 * i5. Но въвеждането на тези формули в работен лист за шест продукта отнема много време. ПреДставете си колко време ще ви е необходимо, ако работите с фирма, която е произвеждала например продукти на 50 в тяхното растение. Много по-лесен начин да изчислите употребата на труда и суровината е да копирате от Г14 на D15 формулата SUMPRODUCT ($D $2: $I $2, D4: i4). Тази формула изчислява D2 * D4 + Е2 * E4 + F2 * F4 + G2 * G4 + Н2 * H4 + I2 * i4 (което е нашата употреба на труда), но е много по-лесно да се влезе! ЗаБележете, че използвам знака $ с диапазона D2: I2, така че когато копирам формулата, все още да улавям продуктовия микс от ред 2. Формулата в клетка D15 изчислява употребата на сурови материали.
По подобен начин печалбата ни се определя от
(Наркотик 1 печалба за паунд) * (наркотик 1 паунда) + (наркотици 2 печалба за паунд) * (наркотици 2 паунда) +... (Наркотици 6 печалба за паунд) * (наркотици 6 паунда)
Печалбата лесно се изчислява в клетка D12 с формулата SUMPRODUCT (D9: I9, $D $2: $I $2).
Сега можем да идентифицираме трите компонента на нашия модел на Solver за продуктов микс.
-
Целева клетка.Нашата цел е да максимизираме печалбата (изчислена в клетка D12).
-
Промяна на клетки.Броят на паундите, произведени от всеки продукт (в списъка в диапазона от клетки D2: I2)
-
Ограничения. Ние имаме следните ограничения:
-
Не използвайте повече труд или суровина, отколкото е налично. Това означава, че стойностите в клетки Г14: D15 (ресурсите, използвани) трябва да бъдат по-малки или равни на стойностите в клетките F14: F15 (наличните ресурси).
-
Да не се произвежда повече от един наркотик, отколкото е в търсенето. Това означава, че стойностите в клетките D2: I2 (паунда, произведено от всяко лекарство) трябва да бъдат по-малки или равни на търсенето за всеки наркотик (в клетка D8: I8).
-
Не можем да генерираме негативен размер на който и да е медикамент.
-
Ще ви покажем как да влезете в целевата клетка, да променяте клетки и ограничения в Solver. След това всичко, което трябва да направите, е да щракнете върху бутона реши, за да намерите продуктовия микс за оптимизиране на печалбата!
За да започнете, щракнете върху раздела данни и в групата анализ щракнете върху Solver.
Забележка: Както е обяснено в глава 26, "Въведение в оптимизацията с Solver за Excel", се инсталира Solver чрез щракване върху бутона Microsoft Office, а след това с опции на Excel, последвани от добавки. В списъка управление щракнете върху добавки на Excel, поставете отметка в полето добавка Solver и след това щракнете върху OK.
Ще се покаже диалоговият прозорец параметри на Solver, както е показано на фигура 27-2.
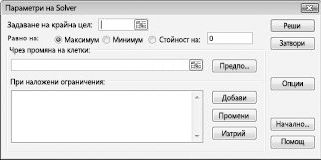
Щракнете върху полето Задай целева клетка и след това изберете нашата клетка за печалба (клетка D12). Щракнете върху полето чрез промяна на клетки и след това посочете диапазона D2: I2, който съдържа паунда, произведено от всеки наркотик. В диалоговия прозорец сега трябва да изглежда фигура 27-3.
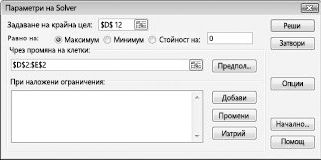
Сега сме готови да добавим ограничения за модела. Щракнете върху бутона Добави. Ще видите диалоговия прозорец Добавяне на ограничение, показан на фигура 27-4.
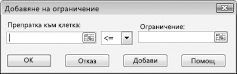
За да добавите ограниченията за използване на ресурсите, щракнете върху полето препратка към клетка и след това изберете диапазона Г14: D15. Изберете < = от средния списък. Щракнете върху полето ограничение и след това изберете диапазона от клетки F14: F15. В диалоговия прозорец Добавяне на ограничения сега трябва да изглежда като фигура 27-5.
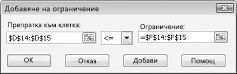
Сега се гарантира, че когато Solver се опитва да използва различни стойности за променливите клетки, само комбинации, които отговарят както на D14< = F14 (използван труд е по-малко или равно на наличната работна ръка), и D15< = F15 (суровината е по-малка или равна на ще бъдат разгледани наличните сурови материали). Щракнете върху Добавяне, за да въведете ограничения за търсенето. Попълнете диалоговия прозорец Добавяне на ограничения, както е показано на фигура 27-6.
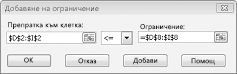
Добавянето на тези ограничения гарантира, че когато Solver изпробва различни комбинации за променливите стойности на клетките, ще бъдат разгледани само комбинации, които отговарят на следните параметри:
-
D2< = D8 (количеството, произведено от наркотик 1, е по-малко или равно на търсенето на наркотик 1)
-
E2< = Е8 (размерът на произведеното на наркотици 2 е по-малък или равен на търсенето на наркотици 2)
-
F2< = F8 (количеството, което е произведено от наркотик 3, е по-малко или равно на търсенето на наркотици 3)
-
G2< = Г8 (количеството, което е произведено от наркотик 4, е по-малко или равно на търсенето на наркотици 4)
-
H2< = H8 (количеството, произведено от наркотик 5, е по-малко или равно на търсенето на наркотици 5)
-
I2< = I8 (количеството, което е произведено от наркотик 6, е по-малко или равно на търсенето на наркотици 6)
Щракнете върху OK в диалоговия прозорец Добавяне на ограничение. Прозорецът Solver трябва да изглежда като фигура 27-7.
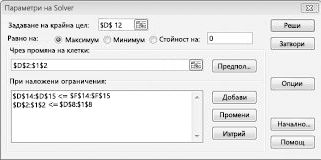
Въвеждаме ограничението, че промяната на клетките трябва да не е отрицателна в диалоговия прозорец Опции на Solver. Щракнете върху бутона "Опции" в диалоговия прозорец параметри на Solver. Поставете отметка в квадратчето Приеми линеен модел и полето Приеми неОтрицателно, както е показано на фигура 27-8 на следващата страница. Щракнете върху OK.
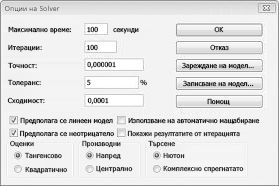
Ако отметнете квадратчето Приемай неОтрицателно, това Solver разглежда само комбинации от променящи се клетки, в които всяка промяна на клетка поема неотрицателна стойност. Проверихме полето поемане на линеен модел, защото проблемът с продуктовия микс е специален тип проблем със Solver, наречен линеен модел. По същество моделът Solver е линеен при следните условия:
-
Целевата клетка се изчислява чрез сумиране на условията във формуляра (промяна на клетка) * (константа).
-
Всяко ограничение отговаря на изискването за линеен модел. Това означава, че всяко ограничение се изчислява, като съберете условията във формуляра (промяна на клетка) * (константа) и сравнявате сумите с константа.
Защо този проблем с Solver е линеен? Нашата целева клетка (печалба) се изчислява като
(Наркотик 1 печалба за паунд) * (наркотик 1 паунда) + (наркотици 2 печалба за паунд) * (наркотици 2 паунда) +... (Наркотици 6 печалба за паунд) * (наркотици 6 паунда)
Това изчисление следва шаблон, в който стойността на целевата клетка се извлича чрез сумиране на термини във формуляра (промяна на клетка) * (константа).
Нашата принуда за труд се изчислява чрез сравняване на стойността, получена от (използва се за паунд от наркотик 1) * (наркотик £ 1) + (труда се използва за паунд на наркотици 2) * (наркотици 2 паунда) +... (Труда ниED за паунд от наркотиците 6) * (наркотици 6 паунда) към наличната работна ръка.
Следователно, ограничението за труд се изчислява чрез събиране на условията във формуляра (промяна на клетка) * (константа) и сравняване на суми към константа. Както ограничението за труд, така и ограничението за сурови материали отговарят на изискването за линеен модел.
Нашите ограничения за търсенето приемат формуляра
(Наркотик 1, произведено) < = (наркотик 1 търсенето) (наркотик 2, произведено) < = (наркотици 2) § (наркотик 6, произведено) < = (наркотици 6 търсенето)
Всяко ограничение за търсенето отговаря на изискването за линеен модел, тъй като всеки е оценен чрез събиране на условията във формуляра (промяна на клетка) * (константа) и сравняване на суми към константа.
След като сте показали, че нашият модел за продуктов микс е линеен модел, защо трябва да ни е грижа?
-
Ако модел на Solver е линеен и изберете поемане на линеен модел, Solver е гарантиран, за да намери оптималното решение за модела на Solver. Ако модел на Solver не е линеен, Solver може или не може да намери оптималното решение.
-
Ако модел на Solver е линеен и изберете поемане на линеен модел, Solver използва много ефикасен алгоритъм (Методът симплекс), за да намери оптималното решение на модела. Ако модел на Solver е линеен и не избираме поемане на линеен модел, Solver използва много неефективен алгоритъм (Методът GRG2) и може да е трудно да намери оптималното решение на модела.
След като щракнете върху OK в диалоговия прозорец Опции на Solver, се връщаме към основния диалогов прозорец на Solver, показан по-рано в фигура 27-7. Когато щракнете върху реши, Solver изчислява оптимално решение (ако има такъв) за нашия модел на продуктов микс. Както посочих в глава 26, оптимално решение за модела за продуктов микс ще бъде набор от променени стойности на клетки (паунда, произведено за всеки наркотик), което увеличава печалбата над набора от всички възможни решения. Отново осъществимо решение е набор от промени в стойностите на клетките, които отговарят на всички ограничения. Променливите стойности на клетките, показани в фигура 27-9, са осъществимо решение, тъй като всички производствени нива са неотрицателни, нивата на производство не надвишават търсенето, а използването на ресурсите не надвишава наличните ресурси.
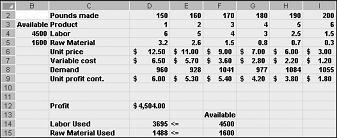
Променливите стойности на клетките, показани на фигура 27-10 на следващата страница, представляват неприложимо решение поради следните причини:
-
Ние произвеждаме повече от наркотици 5 от търсенето за тях.
-
Ние използваме повече труд от това, което е налично.
-
Използваме по-сурови материали от това, което е налично.
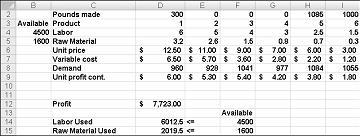
След щракване върху "решаване" Solver бързо намира оптималното решение, показано на фигура 27-11. Трябва да изберете запазване на решението на Solver, за да запазите оптималното стойности на решението в работния лист.
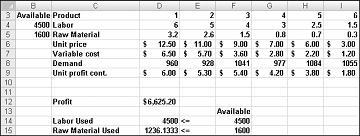
Нашата фирма за наркотици може да увеличи своята месечна печалба на ниво $6 625,20, като произвежда 596,67 паунда на наркотици 4, 1084 паунда на наркотици 5 и нито една от другите лекарства! Не можем да определим дали ще постигнем максималната печалба на $6 625,20 по други начини. Всички ние можем да сме сигурни, че с нашите ограничени ресурси и търсене няма начин да направите повече от $6 627,20 този месец.
Да предположим, че търсенето на всеки продукт трябва да бъде изпълнено. (Вижте неОсъществимия работен лист с решение във файла Prodmix. xlsx.) След това трябва да променим нашите ограничения за търсенето от D2: I2< = D8: I8 към D2: I2> = D8: I8. За да направите това, отворете Solver, изберете D2: I2< = D8: I8 ограничения и след това щракнете върху промяна. Показва се диалоговият прозорец промяна на ограничение, показан на фигура 27-12.
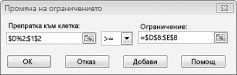
Изберете > = и след това щракнете върху OK. Сега се гарантира, че Solver ще обмисли промяна само на стойности на клетки, които отговарят на всички изисквания. Когато щракнете върху реши, ще видите съобщението "Solver не можа да намери осъществимо решение." Това съобщение не означава, че сме направили грешка в нашия модел, а по-скоро с нашите ограничени ресурси, не можем да отговорим на търсенето за всички продукти. Solver просто ни казва, че ако искаме да отговорим на търсенето за всеки продукт, трябва да добавим още труд, по-сурови материали или повече от двете.
Да видим какво ще се случи, ако разрешим неограничено търсене за всеки продукт и разрешаваме да се произведат отрицателни количества за всеки наркотик. (Можете да видите този проблем със Solver върху ЗададениТе стойности не събират работния лист във файла Prodmix. xlsx.) За да намерите оптималното решение за тази ситуация, отворете Solver, щракнете върху бутона Опции и изчистете отметката от квадратчето Приеми неОтрицателните. В диалоговия прозорец параметри на Solver изберете ограничения за търсенето D2: I2< = D8: I8 и след това щракнете върху Изтрий, за да премахнете ограничението. Когато щракнете върху реши, Solver връща съобщението "Задаване на стойности на клетки не се събират." Това съобщение означава, че ако целевата клетка трябва да бъде увеличена (както е в нашия пример), има осъществими решения с произволно големи стойности на целевите клетки. (Ако целевата клетка трябва да бъде намалена, съобщението "Задаване на стойности на клетки не съвпадат" означава, че има осъществими решения с произволно малки стойности на целевата клетка.) В нашата ситуация, като позволим отрицателно производство на наркотик, ние действаме "създаване на" ресурси, които могат да се използват за производство на произволно големи количества други лекарства. Предвид нашите неограничени изисквания, това ни позволява да реализираме неограничени печалби. В ситуация, в която не може да се направи безкраен размер пари. Накратко, ако виждате "Задаване на стойности, които не се събират", моделът ви има грешка.
-
Да предположим, че нашата фирма за лекарства може да закупи до 500 часа труд при $1 повече на час от текущите разходи за труд. Как можем да максимизираме печалбата?
-
В завод за производство на чипове четирите техници (A, B, C и D) произвеждат три продукта (продукти 1, 2 и 3). Този месец доставчикът на чип може да продаде 80 единици на продукт 1, 50 на продукти 2 и в повечето 50 единици на продукт 3. Техник А може да направи само продукти 1 и 3. Техник Б може да направи само продукти 1 и 2. Техник В може да направи само продукт 3. Техник Д може да направи само продукт 2. За всяка произведена единица продуктите допринасят за следващата печалба: продукт 1; $6; Продукт 2; $7; и продукт 3, $10. Времето (в часове), всеки техник трябва да произвежда продукт, е както следва:
Продукт
Техник А
Техник Б
Техник В
Техник Д
1
2
2,5
Не можете да направите
Не можете да направите
2
Не можете да направите
3
Не можете да направите
3,5
3
3
Не можете да направите
4
Не можете да направите
-
Всеки техник може да работи до 120 часа месечно. Как производителя на чипове ще увеличи своята месечна печалба? Да предположим, че може да се произведе дробен брой единици.
-
Завод за производство на компютри произвежда мишки, клавиатури и джойстикове за видеоигри. В таблицата по-долу са дадени печалбата за единица производителност, за единица труд за всеки отделен човек, за месечната потребност и за единица машина – времето на използване:
Мишки
Клавиатури
Джойстици
Печалба/единица
$8
$11
$9
Трудова употреба/единица
.2 часа
.3 часа
.24 часа
Машина за време/единица
.04 Hour
.055 Hour
.04 Hour
Месечно търсене
15 000
27 000
11 000
-
Всеки месец са налични общо часове за труд на 13 000 и 3000 часа на машинното време. Как производителя може да увеличи своя месечен принос за печалбата от растението?
-
Разрешаване на нашия пример за наркотици, ако предположим, че трябва да се изпълнят минимални изисквания на 200 за всеки наркотик.
-
Jason прави диамантени гривни, колиета и обеци. Иска да работи най-много за 160 часа на месец. Има 800 унции диаманти. По-долу са дадени печалби, време на труда и унции диаманти, необходими за производството на всеки продукт. Ако търсенето за всеки продукт е неограничено, как Джейсън ще увеличи печалбата си?
Продукт
Печалба за единица
Часове за труд за единица
Унции диаманти за единица
Гривна
300 лв.
.35
1,2
Огърлица
200 лв.
.15
.75
Обиците
100 лв.
0,05
0,5










