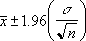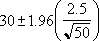Връща доверителния интервал за средната стойност на генералната съвкупност с нормално разпределение. Доверителният интервал е диапазон от двете страни на средната стойност на извадката. Например ако поръчате продукт по пощата, можете да определите с особено ниво на увереност най-ранните и най-новите продукти ще пристигнат.
Синтаксис
CONFIDENCE(алфа;standard_dev;размер)
"алфа" е нивото на значимост, използвано за изчисляване на доверителното ниво. Доверителното ниво е равно на 100*(1 – алфа)%, или с други думи, алфа, равно на 0,05, означава 95 процента доверително ниво.
"стандартно_откл" е стандартното отклонение на генералната съвкупност за диапазона от данни и се приема за известно.
Размер е размерът на извадката.
Забележки
-
Ако някой аргумент е нечислови, CONFIDENCE връща #VALUE! стойността на грешка.
-
Ако алфа ≤ 0 или алфа ≥ 1, CONFIDENCE връща #NUM! стойността на грешка.
-
Ако standard_dev ≤ 0, CONFIDENCE връща #NUM! стойността на грешка.
-
Ако "размер" не е цяло число, дробната му част се отрязва.
-
Ако размер < 1, CONFIDENCE връща #NUM! стойността на грешка.
-
Ако приемем, че "алфа" е равно на 0,05, трябва да изчислим площта под кривата на стандартното нормално разпределение, която се равнява на (1 – алфа), или 95 процента. Тази стойност е ± 1,96. Следователно доверителният интервал е:
Пример
Да предположим, че в нашата извадка от 50 души, средната дължина на пътуването до работа е 30 минути със стандартно отклонение на генералната съвкупност от 2,5. Можем да сме 95 процента уверени, че средната стойност на генералната съвкупност е в интервала:
|
"алфа" |
Стандартно отклонение |
Размер |
Формула |
Описание (Резултат) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENCE([Алфа];[StdDev];[Размер]) |
Доверителен интервал на средната стойност на генералната съвкупност. С други думи, средната дължина на пътуването до работното място е равна на 30 ± 0,692951 минути или от 29,3 до 30,7 минути. (0.692951) |