LINEST функция

Описание

Функцията LINEST изчислява статистиките за линия с помощта на метода на най-малките квадрати, за да намери правата линия, която най-добре се съгласува с вашите данни, и връща масив, който описва линията. Освен това можете да комбинирате LINEST с други функции, за да изчислите статистиката за други типове модели, които са линейни при неизвестните параметри, включително полиномни, логаритмични, експоненциални и на степенни редове. Тъй като тази функция връща масив от стойности, тя трябва да бъде въведена като формула за масив. Инструкциите са по реда на примерите в тази статия.

Уравнението за линията е:

y = mx + b

–или–

y = m1x1 + m2x2 + ... + b

ако има множество диапазони от x-стойности, където зависимите стойности на y са функция на независимите стойности на x. Стойностите m са коефициенти, съответстващи на всяка стойност на x, а b е константа. Забележете, че y, x и m могат да са вектори. Масивът, който функцията LINEST връща, е {mn,mn-1,...,m1,b}. LINEST може да върне и допълнителни регресионни статистики.

Синтаксис

LINEST(известни_y; [известни_x]; [конст]; [състояния])

Синтаксисът на функцията LINEST има следните аргументи:

Синтаксис

• известни_y    Задължително. Наборът от стойности на y в отношението y = mx + b, които вече знаете.

  • Ако диапазонът на известни_y е в една колона, всяка колона от известни_x се разглежда като отделна променлива.

  • Ако диапазонът на известни_y се съдържа в един ред, всеки ред на известни_x се разглежда като отделна променлива.

• известни_x    Незадължително. Набор от стойности на x в отношението y = mx + b, които вече знаете.

  • Диапазонът известни_x може да включва един или повече набори от променливи. Ако се използва само една променлива, известни_y и известни_x могат да бъдат диапазони с произволна форма, стига да имат еднакви размерности. Ако се използва повече от една променлива, известни_y трябва да бъде вектор (т. е. диапазон с височина от един ред или ширина от един колона).

  • Ако известни_x е пропуснато, вместо него се използва масивът {1,2,3,...} със същия размер като известни_y.

• конст    Незадължително. Логическа стойност, задаваща дали константата b да се изравни на 0.

  • Ако конст е TRUE или е пропуснато, b се изчислява нормално.

  • Ако конст е FALSE, b се задава равно на 0 и m-стойностите се нагласяват така, че да се съгласуват с y = mx.

• състояния    Незадължително. Логическа стойност, задаваща дали да се върнат допълнителни регресионни статистики.

  • Ако статистиката е TRUE, LINEST връща допълнителната регресионна статистика; в резултат върнатият масив е {mn,mn-1,...,m1;b;sen,sen-1,...,se1;seb;r²,sey; F,df;ssreg,ssresid}.

  • Ако състояния е FALSE или пропуснат, LINEST връща само коефициентите m и константата b.

    Допълнителните регресионни статистики са като следва.

Следващата илюстрация показва реда, в който се връщат допълнителните регресионни статистики.

Забележки

• Всяка права линия може да се опише с наклона й и точката, в която пресича оста y:

  Наклон (m):
  За да намерите наклона на линия, често написана като m, вземете две точки на линията, (x1,y1) и (x2,y2); наклонът е равен на (y2 - y1)/(x2 - x1).

  Прихващане на Y (b):
  Прихващането на линия, често написано като b, е стойността на y в точката, където линията пресича оста y.

  Уравнението на права линия е y = mx + b. След като знаете стойностите на m и b, можете да изчислите всяка точка от линията, като поставите в това уравнение стойността на y или x. Можете също да използвате функцията TREND.

• Когато имате само една независима променлива x, можете да получите стойностите на наклона и пресечната точка директно с помощта на следните формули:

  Наклон:
  =INDEX(LINEST(known_y,known_x),1)

  Прихващане на Y:
  =INDEX(LINEST(known_y,known_x),2)

• Точността на изчислената с LINEST линия зависи от степента на разсейване във вашите данни. Колкото по-линейни са данните, толкова по-точен е моделът LINEST . LINEST използва метода на най-малките квадрати, за да определи най-доброто съгласуване с данните. Когато имате само една независима променлива x, изчисленията за m и b се основават на следните формули:

  

  

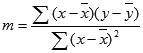
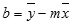
  където x и y са средни стойности, т. е. x = AVERAGE(известни_x) и y = AVERAGE(известни_y).

• Функциите за линейно-и извито прилепване LINESTи LOGEST могат да изчислят най-добрата права линия или експоненциална крива, която отговаря на вашите данни. Трябва обаче да решите кой от двата резултата най-добре отговаря на вашите данни. Можете да изчислите TREND(known_y,known_x) за права линия или GROWTH(known_y,known_x) за експоненциална крива. Тези функции, без аргумента на new_x, връщат масив от стойности на y, прогнозирани по тази линия или крива в действителните точки от данни. След това можете да сравните прогнозираните стойности с действителните стойности. Може да искате да ги на диаграма и двете за визуално сравнение.

• В регресионния анализ Excel изчислява за всяка точка повдигнатата на квадрат разлика между стойността на y, оценена за тази точка, и действителната стойност на y. Сумата на тези повдигнати на квадрат разлики се нарича остатъчна сума от квадрати, ssresid. След това Excel изчислява общата сума от квадрати, sstotal. Когато аргументът конст = TRUE или е пропусната, общата сума от квадрати е сумата на повдигнатите на квадрат разлики между действителните стойности на y и средната стойност на отделните стойности на y. Когато аргументът конст = FALSE, общата сума от квадрати е сумата на квадратите на действителните стойности на y (без да се изважда средната стойност на y от всяка отделна стойност на y). Тогава може да се намери регресионната сума от квадрати, ssreg, като: ssreg = sstotal – ssresid. Колкото по-малка е^{остатъчната}сума от квадрати в сравнение с общата сума на квадратите, толкова по-голяма е стойността на коефициента на определяне, r 2 , което е индикатор за това колко добре уравнението, получено от регресионния анализ, обяснява отношението между променливите. Стойността на r^{2 е} равна на ssreg/sstotal.

• В някои случаи една или повече от колоните X (да предположим, че колоните на Y и X) може да нямат допълнителна прогнозна стойност в присъствието на другите X колони. С други думи, премахването на една или повече X колони може да доведе до прогнозирани стойности на Y, които са еднакво точни. В този случай тези излишни X колони трябва да бъдат пропуснати от регресионния модел. Това явление се нарича "колинеарност", тъй като всяка съкратена колона X може да се изрази като сума от кратни стойности на колоните X, които не са излишни. Функцията LINEST проверява за колинеарност и премахва излишните X колони от регресионния модел, когато ги идентифицира. Премахнатите X колони могат да бъдат разпознати в изходната линия LINEST като имащи 0 коефициента в допълнение към стойностите 0 se. Ако една или повече колони са премахнати като излишни, df се засяга, тъй като df зависи от броя на X колоните, действително използвани за предсказващи цели. За подробности относно изчисляването на df вж. Пример 4. Ако df се променя, защото се премахват излишните X колони, стойностите на sey и F също се засягат. Колинеарността трябва да е сравнително рядка на практика. Обаче един случай, в който е по-вероятно да възникне, е когато някои X колони съдържат само 0 и 1 стойности като индикатори дали дадена тема в експеримент е или не е член на определена група. Ако const = TRUE или е пропуснато, функцията LINEST ефективно вмъква допълнителна X колона с всички 1 стойности, за да моделизирува пресечната точка. Ако имате колона с 1 за всяка тема, ако е мъж, или 0, ако не, и също така имате колона с 1 за всяка тема, ако е жена, или 0, ако не, последната колона е излишна, тъй като записите в нея могат да бъдат получени от изваждането на записа в колоната "мъжки индикатор" от записа в допълнителната колона на всички 1 стойности, добавени от функцията LINEST.

• Когато от модела не са премахнати колони за X поради колинеарност, стойността на df се изчислява по следния начин: ако има k колони от известни_x и конст = TRUE или е пропуснато, df = n – k – 1. Ако конст = FALSE, df = n – k. И в двата случая всяка колона за X, премахната поради колинеарност, увеличава стойността на df с 1.

• Когато въвеждате като аргумент масив от константи (като известни_x), използвайте запетаи за отделяне на стойностите, съдържащи се в един и същ ред, и точка и запетая за отделяне на различните редове. Разделителните знаци могат да се различават, в зависимост от вашите регионални настройки

• Забележете, че стойностите на y, прогнозирани от регресионното уравнение, може да не са валидни, ако са извън диапазона на стойностите на y, който сте използвали, за да дефинирате уравнението.

• Алгоритъмът, на който се базира функцията LINEST, е различен от този, който се използва във функциите SLOPE и INTERCEPT. Разликата в тези алгоритми може да доведе до различни резултати, когато данните са неопределени и колинеарни. Ако например точките на данните на аргумента известни_y са 0 и точките за данни на аргумента известни_x са 1:

  • LINEST връща стойност 0. Алгоритъмът на функцията LINEST е проектиран да връща смислени резултати за колинеарни данни и в този случай може да се намери поне един отговор.

  • SLOPE и INTERCEPT връщат #DIV/0! грешка. Алгоритъмът на функциите SLOPE и INTERCEPT е предназначен да търси само един отговор и в този случай може да има повече от един отговор.

• В допълнение към използването на LOGEST за пресмятане на статистики за други типове регресии, можете да използвате LINEST, за да пресмятате диапазон на други типове регресии, въвеждайки променливите x и y като x и y серии за LINEST. Например формулата:

  =LINEST(yстойности, xстойности^COLUMN($A:$C))

  работи, когато имате единична колона от y-стойности и единични колона от x-стойности, за да изчислите кубично (полином от трета степен) приближение в следната форма:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Можете да настроите тази формула за да изчислява други типове регресии, но в някои случаи тя изисква настройка на изходящите стойности и други статистики.

• Стойността на F-теста, която е върната от функцията LINEST се различава от стойността на F-теста, връщана от функцията FTEST. LINEST връща F статистика, докато FTEST връща вероятността.

Примери