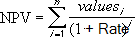NPV функция

Синтаксис

NPV(ставка;стойност1;стойност2;...)

Ставка     е дисконтовата ставка за един период.

Стойност1; стойност2,...     са от 1 до 29 аргумента, представляващи плащанията и приходите. Стойност1; стойност2,... трябва да бъдат с равно разстояние във времето и да се появяват в края на всеки период. NPV използва реда на стойност1, стойност2,... за да се определи редът на паричните потоци. Уверете се, че въвеждате стойностите на плащанията и приходите в правилния ред. Броят се аргументите, които са числа, празни, логически стойности или текстово представяне на числа; аргументи, които са стойности за грешки или текст, който не може да бъде преведен в числа, се игнорират.

Забележки

• NPV инвестицията започва един период преди датата на паричния поток стойност1 и завършва с последния паричен поток в списъка. Изчислението на NPV е на базата на бъдещи парични потоци. Ако вашият първи паричен поток е в началото на първия период, първата стойност трябва да се добави към резултата от NPV, който не е включен в аргументите. За повече информация вж. примерите по-долу.

• Ако n е броят на паричните потоци в списъка от стойности, формулата за NPV е:

  

• NPV е подобна на функцията PV (настояща стойност). Основната разлика между PV и NPV е, че PV позволява паричните потоци да започват или в края, или в началото на периода. За разлика от променливата NPV стойности на паричните потоци, паричните потоци на PV трябва да са постоянни по време на инвестицията. За информация относно анюитетите и финансовите функции вж. PV.

Пример 1

В следващия пример:

• Ставка е годишната дисконтова ставка.

• Стойност1 е началната стойност на инвестицията една година след днешната дата.

• Стойност2 е доходът от първата година.

• Стойност3 е доходът от втората година.

• Стойност4 е доходът от третата година.

В примера включвате първоначалната цена от 10 000 лв. като една от стойностите, защото плащането се извършва в края на първия период.

Пример 2

В следващия пример:

• Ставка е годишната дисконтова ставка. Това може да представя процента на инфлацията или лихвения процент на конкурентна инвестиция.

• Стойност1 е началната стойност на инвестицията една година след днешната дата.

• Стойност2 е доходът от първата година.

• Стойност3 е доходът от втората година.

• Стойност4 е доходът от третата година.

• Стойност5 е доходът от четвъртата година.

• Стойност6 е доходът от петата година.

В примера не включвате първоначалната цена от 40 000 лв. като една от стойностите, защото плащането се извършва в началото на първия период.