В тази статия е описан синтаксисът и употребата на функцията ODDLYIELD в Microsoft Excel.
Описание
Връща дохода за ценна книга, която има нерегулярен (кратък или дълъг) последен период.
Синтаксис
ODDLYIELD(разчет; погасяване; последна_лихва; ставка; цена; изкупуване; честота; [база])
Важно: Датите трябва да бъдат въведени с помощта на функцията DATE или като резултати на други формули или функции. Например използвайте DATE(2008;5;23) за 23-ия ден на май 2008 г. Проблеми може да възникнат, ако датите са въведени като текст.
Синтаксисът на функцията ODDLYIELD има следните аргументи:
-
Разчет Задължително. Датата на сделката с ценната книга. Датата на сделката е датата след датата на издаване, когато книгата е продадена на купувача.
-
Погасяване Задължително. Датата на падежа на ценната книга. Датата на падежа е датата, когато срокът на книгата изтича.
-
Последна_лихва Задължително. Датата на първия купон на ценната книга.
-
Ставка Задължително. Лихвеният процент на ценната книга.
-
"цена" Задължително. Цената на ценната книга.
-
Изкупуване Задължително. Погасителната стойност на книгата за $100 номинална стойност.
-
Честота Задължително. Броят на купонните плащания за година. За годишни плащания честота = 1; за шестмесечни честота = 2; за тримесечни честота = 4.
-
База Незадължително. Типът на годишната база, която се използва.
|
База |
Брой на дните |
|---|---|
|
0 или пропуснато |
US (NASD) 30/360 |
|
1 |
Действителен/действителен |
|
2 |
Действителен/360 |
|
3 |
Действителен/365 |
|
4 |
Европейска 30/360 |
Забележки
-
Microsoft Excel съхранява датите като поредни числа, така че те могат да се използват в изчисления. По подразбиране 1 януари 1900 е с поредно число 1, а 1 януари 2008 е с поредно число 39448, понеже той е 39 448 дни след 1 януари 1900.
-
Датата на сделката е датата, когато един купувач закупи купон, например облигация. Датата на падежа е датата, когато купонът изтича. Нека например една 30-годишна облигация да е издадена на 1 януари 2008 г. и закупена от купувач шест месеца по-късно. Датата на издаване ще бъде 1 януари 2008 г., датата на сделката – 1 юли 2008 г, а датата на падежа – 1 януари 2038 г., 30 години след 1 януари 2008 г., датата на издаване.
-
Разчет, погасяване, последна_лихва и база се закръгляват надолу до цели числа.
-
Ако разчет, погасяване или last_interest не е валидна дата, ODDLYIELD връща #VALUE! стойността на грешка.
-
Ако ставка < 0 или ако pr ≤ 0, ODDLYIELD връща #NUM! стойността на грешка.
-
Ако база < 0 или база > 4, ODDLYIELD връща #NUM! стойността на грешка.
-
Трябва да бъде изпълнено следното условие за дата; в противен случай ODDLYIELD връща #NUM! стойност на грешка:
погасяване > разчет > последна_лихва
-
ODDLYIELD се изчислява по следния начин:
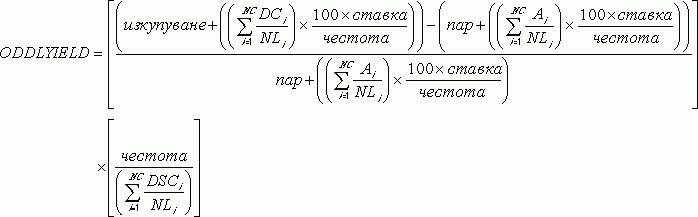
където:
-
Ai = брой на изтеклите дни за i-я, или последен, квазикупонен период в нерегулярния период, броейки напред от последната дата на олихвяване преди погасяването.
-
DCi = брой на дните, броени в i-я, или последен, квазикупонен период, ограничени от дължината на действителния купон период.
-
NC = брой на квазикупонните периоди, които се побират в нерегулярния период; ако това число съдържа дроб, то се закръглява към следващото цяло число.
-
NLi = нормална дължина в дни на i-я, или последния, квазикупонен период в нерегулярния купонен период.
-
Пример
Копирайте примерните данни в следващата таблица и ги поставете в клетка A1 на нов работен лист на Excel. За да покажат резултати формулите, изберете ги, натиснете клавиша F2 и след това натиснете клавиша Enter. Ако е необходимо, коригирайте ширините на колоните, за да видите всичките данни.
|
Данни |
Описание на аргумента |
|
|---|---|---|
|
20.04.2008 |
Дата на разчета |
|
|
15.06.2008 |
Дата на погасяване |
|
|
24.12.2007 |
Дата на последно изплащане на лихвата |
|
|
3,75% |
Процент на купона |
|
|
99,875 лв. |
Цена |
|
|
100 лв. |
Погасителна стойност |
|
|
2 |
Честотата е полугодишна |
|
|
0 |
30/360 база |
|
|
Формула |
Описание |
Резултат |
|
=ODDLYIELD(A2; A3; A4; A5; A6; A7; A8; A9) |
Доходността на ценна книга, която има нечетен (кратък или дълъг) първи период, за облигация с използване на условията в клетки A2:A10 като аргументи на функцията. Резултатът е 0,04519 или 4,52%. |
4,52% |










