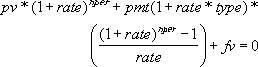BW-Funktion

Syntax

PV(rate,nper,pmt,fv,type)

Zins     ist der Zinssatz pro Zeitraum. Wenn Sie z. B. einen Kredit für ein Auto mit einem jährlichen Zinssatz von 10 Prozent erhalten und monatliche Zahlungen leisten, beträgt der Zinssatz pro Monat 10 %/12 oder 0,83 %. Sie geben „10 %/12“ oder „0,83 %“ oder „0,0083“ als Rate in die Formel ein.

Zzr     ist die Gesamtzahl der Zahlungszeiträume in einer Annuität. Wenn Sie beispielsweise einen 4 Jahre laufenden Kredit für ein Auto erhalten und monatliche Zahlungen leisten, weist ihr Darlehen 4 * 12 (also 48) Zeiträume auf. Sie geben „48“ in die Formel für Nper ein.

RMZ     ist die Zahlung, die für jeden Zeitraum geleistet wird und sich während der Lebensdauer der Annuität nicht ändern kann. In der Regel umfasst RMZ Prinzipal- und Zinszahlungen, aber keine anderen Gebühren oder Steuern. Beispielsweise betragen die monatlichen Zahlungen für einen vierjährigen Auto-Kredit für 10.000 US-Dollar mit 12 Prozent Zinsen 263,33 US-Dollar. Sie geben „-263.33“ in die Formel als RMZ ein. Wenn „RMZ“ ausgelassen wird, müssen Sie das Argument „Zw“ verwenden.

Zw     ist der zukünftige Wert oder ein Barguthaben, das Sie nach der letzten Zahlung erreichen möchten. Fehlt das Argument "Zw", wird es als 0 angenommen (beispielsweise ist der Endwert eines Kredits gleich 0). Wenn Sie beispielsweise 50.000 USD sparen möchten, um für ein spezielles Projekt in 18 Jahren zu bezahlen, ist 50.000 USD der zukünftige Wert. Sie können dann eine vorsichtige Schätzung zu einem Zinssatz treffen und bestimmen, wie viel Sie jeden Monat sparen müssen. Wenn "Zw" ausgelassen wird, müssen Sie das Argument "Rmz" verwenden.

F     ist die Zahl 0 oder 1 und gibt an, wann Zahlungen fällig sind.

Hinweise

• Stellen Sie sicher, dass Sie für Zins und Zzr zueinander passende Zeiteinheiten verwenden. Wenn Sie für einen Kredit mit vierjähriger Laufzeit und einer jährlichen Verzinsung von 12% monatliche Zahlungen leisten, müssen Sie für Zins 12%/12 und für Zzr 4*12 angeben. Wenn Sie für den gleichen Kredit jährliche Zahlungen leisten, müssen Sie für Zins 12% und für Zzr 4 angeben.

• Die folgenden Funktionen gelten für Annuitäten: FV; ZINSZ; RMZ; KAPZ; PV; und RATE. Eine Annuität ist eine Reihe von konstanten Barzahlungen, die in einem fortlaufenden Zeitraum geleistet werden. Beispielsweise ist ein Kredit für ein Auto oder eine Hypothek eine Annuität. Weitere Informationen finden Sie in der Beschreibung der einzelnen Annuitätsfunktionen.

• Bei Annuitätsfunktionen gilt, dass Geldbeträge, die Sie auszahlen (zum Beispiel eine Spareinlage), durch negative Zahlen und Geldbeträge, die Sie einnehmen (zum Beispiel Dividenden), durch positive Zahlen dargestellt werden. Beispielsweise würde eine Bankeinlage von 1.000 USD durch das Argument -1000 dargestellt, wenn Sie der Einzahler sind, und durch das Argument 1000, wenn Sie die Bank sind.

• Ein finanzielles Argument wird in Bezug auf die anderen gelöst. Wenn die Rate nicht 0 ist, gilt Folgendes:

  

  Ist Zins gleich 0, dann gilt:

  (Rmz * Zzr) + Bw + Zw = 0

Beispiel

Im folgenden Beispiel:

• Pmt ist das Geld, das am Ende jedes Monats aus einer Versicherungsrente gezahlt wird.

• Zinssatz ist der Zinssatz, der auf das ausbezahlte Geld verdient wird.

• Nper ist die Jahre, die das Geld ausbezahlt wird.

Der Zinssatz wird durch 12 geteilt, um eine monatliche Rate zu erhalten. Die Jahre, in der das Geld ausgezahlt wird, wird mit 12 multipliziert, um die Anzahl der Zahlungen zu erhalten.

Das Ergebnis ist negativ, da es Geld darstellt, das Sie zahlen würden, einen ausgehenden Cashflow. Wenn Sie aufgefordert werden, (60.000) für die Annuität zu zahlen, würden Sie feststellen, dass dies keine gute Investition wäre, da der Barwert der Annuität (59.777,15) niedriger ist als der, zu dem Sie aufgefordert werden.