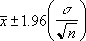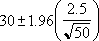Gibt das Konfidenzintervall für einen Auffüllungsmittelwert mit normaler Verteilung zurück. Das Konfidenzintervall ist ein Bereich auf beiden Seiten eines Stichprobenmittelwerts. Wenn Sie beispielsweise ein Produkt über die Post bestellen, können Sie mit einem bestimmten Maß an Vertrauen bestimmen, ob das Produkt am frühesten und letzten eintrifft.
Syntax
CONFIDENCE(alpha,standard_dev,size)
Alpha ist die Signifikanzstufe, die zum Berechnen des Konfidenzniveaus verwendet wird. Das Konfidenzintervall ist gleich 100*(1 - Alpha)%, was bedeutet, dass ein Wert für Alpha von 0,05 einem Konfidenzniveau von 95% entspricht.
Standabwn ist die Standardabweichung der Population für den Datenbereich und wird als bekannt angenommen.
Größe ist die Stichprobengröße.
Hinweise
-
Wenn ein Argument nicht numerisch ist, gibt CONFIDENCE die #VALUE! an.
-
Wenn Alpha ≤ 0 oder Alpha ≥ 1, gibt KONFIDENZ den #NUM! an.
-
Wenn standard_dev ≤ 0 ist, gibt CONFIDENCE den #NUM! an.
-
Ist Umfang keine ganze Zahl, wird der Dezimalanteil abgeschnitten.
-
Wenn größe < 1, gibt CONFIDENCE die #NUM! an.
-
Wenn wir davon ausgehen, dass Alpha 0,05 ist, müssen wir den Bereich unter der Standardnormalkurve berechnen, die gleich (1 - Alpha) oder 95 Prozent ist. Dieser Wert ist ± 1,96. Das Konfidenzintervall lautet daher:
Beispiel
Angenommen, wir stellen fest, dass in unserer Stichprobe von 50 Pendlern die durchschnittliche Fahrt zur Arbeit 30 Minuten mit einer Standardabweichung der Bevölkerung von 2,5 beträgt. Wir können zu 95 Prozent sicher sein, dass der Bevölkerungsmittelwert im Intervall liegt:
|
Alpha |
StdDev |
Größe |
Formel |
Beschreibung (Ergebnis) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENCE([Alpha],[StdDev],[Size]) |
1-Alpha Konfidenzintervall für den Erwartungswert einer Zufallsvariablen. Anders ausgedrückt: Die durchschnittliche Arbeitsreise beträgt 30 ± 0,692951 Minuten oder 29,3 bis 30,7 Minuten. (0.692951) |