Επιστρέφει το διάστημα εμπιστοσύνης για τον μέσο ενός πληθυσμού, χρησιμοποιώντας κανονική κατανομή.
Περιγραφή
Το διάστημα εμπιστοσύνης είναι μια περιοχή τιμών. Η μέση τιμή δείγματος, x, βρίσκεται στο κέντρο αυτής της περιοχής και η περιοχή είναι x ± CONFIDENCE.NORM. Για παράδειγμα, εάν x είναι ο μέσος όρος δείγματος των ωρών παράδοσης για προϊόντα που έχουν παραγγελθει μέσω ηλεκτρονικού ταχυδρομείου, x ± CONFIDENCE. Η συνάρτηση NORM είναι μια περιοχή μέσου πληθυσμού. Για κάθε μέσο πληθυσμού, μ0, σε αυτό το εύρος, η πιθανότητα να ληφθεί μέση τιμή δείγματος πέραν του μ0 από το x είναι μεγαλύτερη από άλφα· για κάθε μέσο πληθυσμού, μ0, όχι σε αυτό το εύρος, η πιθανότητα να ληφθεί μέση τιμή δείγματος πέραν του μ0 από x είναι μικρότερη από άλφα. Με άλλα λόγια, ας υποθέσουμε ότι χρησιμοποιούμε x, standard_dev και μέγεθος για να κατασκευάσουμε έναν δίπυρο έλεγχο σε επίπεδο σημαντικότητας άλφα της υπόθεσης ότι ο μέσος όρος του πληθυσμού είναι μ0. Τότε δεν θα απορρίψουμε αυτή την υπόθεση εάν το μ0 είναι στο διάστημα εμπιστοσύνης και θα απορρίψουμε αυτή την υπόθεση εάν το μ0 δεν είναι στο διάστημα εμπιστοσύνης. Το διάστημα εμπιστοσύνης δεν μας επιτρέπει να συμπεράνουμε ότι υπάρχει πιθανότητα 1 – άλφα ότι το επόμενο πακέτο μας θα λάβει χρόνο παράδοσης που βρίσκεται στο διάστημα εμπιστοσύνης.
Σύνταξη
CONFIDENCE.NORM(άλφα;τυπική_απόκλιση;μέγεθος)
Η σύνταξη της συνάρτησης CONFIDENCE.NORM περιλαμβάνει τα παρακάτω ορίσματα:
-
Άλφα Υποχρεωτικό. Το επίπεδο σημαντικότητας που χρησιμοποιείται για τον υπολογισμό του επιπέδου εμπιστοσύνης. Το επίπεδο εμπιστοσύνης ισούται με 100*(1 - άλφα)%, δηλαδή, μια τιμή άλφα ίση με 0,05 υποδηλώνει επίπεδο εμπιστοσύνης 95 τοις εκατό.
-
Τυπική_απόκλιση Υποχρεωτικό. Η τυπική απόκλιση της περιοχής δεδομένων του πληθυσμού, η οποία θεωρείται γνωστή.
-
Μέγεθος Υποχρεωτικό. Το μέγεθος του δείγματος.
Παρατηρήσεις
-
Εάν κάποιο από τα ορίσματα δεν είναι αριθμητικό, η συνάρτηση CONFIDENCE.NORM επιστρέφει #ΤΙΜΗ! ως τιμή σφάλματος.
-
Εάν άλφα ≤ 0 ή άλφα ≥ 1, η συνάρτηση CONFIDENCE.NORM επιστρέφει #ΑΡΙΘ! ως τιμή σφάλματος.
-
Εάν το όρισμα τυπική_απόκλιση ≤ 0, η συνάρτηση CONFIDENCE.NORM επιστρέφει #ΑΡΙΘ! ως τιμή σφάλματος.
-
Εάν το όρισμα μέγεθος δεν είναι ακέραιος, τα δεκαδικά ψηφία περικόπτονται.
-
Εάν το όρισμα μέγεθος < 1, η συνάρτηση CONFIDENCE.NORM επιστρέφει #ΑΡΙΘ! ως τιμή σφάλματος.
-
Εάν υποθέσουμε ότι το άλφα ισούται με 0,05, πρέπει να υπολογίσουμε την περιοχή κάτω από την τυπική κανονική καμπύλη που ισούται με (1 - άλφα), ή 95 τοις εκατό. Η τιμή αυτή είναι ±1,96. Το διάστημα εμπιστοσύνης είναι συνεπώς:
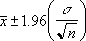
Παράδειγμα
Αντιγράψτε τα δεδομένα του παραδείγματος στον πίνακα που ακολουθεί και, στη συνέχεια, επικολλήστε τα στο κελί A1 ενός νέου φύλλου εργασίας του Excel. Για εμφανιστούν τα αποτελέσματα των τύπων, επιλέξτε τους, πατήστε το πλήκτρο F2 και, στη συνέχεια, πατήστε το πλήκτρο Enter. Αν χρειαστεί, μπορείτε να ρυθμίσετε το πλάτος των στηλών για να βλέπετε όλα τα δεδομένα.
|
Δεδομένα |
Περιγραφή |
|
|
0,05 |
Επίπεδο σημαντικότητας |
|
|
2,5 |
Τυπική απόκλιση του πληθυσμού |
|
|
50 |
Μέγεθος δείγματος |
|
|
Τύπος |
Περιγραφή |
Αποτέλεσμα |
|
=CONFIDENCE.NORM(A2;A3;A4) |
Διάστημα βεβαιότητας του μέσου ενός πληθυσμού. Δηλαδή, το διάστημα εμπιστοσύνης για τον υποκείμενο μέσο πληθυσμού για τη διάρκεια διαδρομής προς την εργασία ισούται με 30 ± 0,692952 λεπτά ή 29,3 με 30,7 λεπτά. |
0,692952 |










