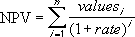NPV

Süntaks

NPV(määr;väärtus1;väärtus2;...)

Määr  on diskontomäär ühe perioodi jooksul.

Väärtus1; väärtus2,...     on 1–29 argumenti, mis tähistavad makseid ja sissetulekut. Väärtus1; väärtus2,... peab olema võrdse vahega ajas ja asetsema iga perioodi lõpus. NPV kasutab väärtuse väärtus2 järjestust,... rahavoogude järjestuse tõlgendamiseks. Veenduge, et sisestate oma makse ja sissetuleku väärtused õiges järjestuses. Argumente, mis on arvud, tühjad loogikaväärtused või arvude tekstiesitused, loendatakse; argumente, mis on veaväärtused või tekst, mida ei saa arvudeks tõlkida, ignoreeritakse.

Märkused.

• Funktsiooni NPV investeering algab üks periood enne rahavoogu väärtus1 ja lõpeb loendi viimase rahavooga. Funktsiooni NPV arvutus põhineb tulevastel rahavoogudel. Kui esimene rahavoog toimub esimese perioodi alguses, tuleb esimene väärtus lisada funktsiooni NPV tulemile, mitte kaasata väärtuste argumentidesse. Lisateabe saamiseks vt näiteid allpool.

• Kui n on rahavoogude arv väärtuste loendis, on funktsiooni NPV valem:

  

• Funktsioon NPV on sarnane funktsiooniga PV (praegune väärtus). Põhiline erinevus funktsioonide PV ja NPV vahel on see, et PV lubab rahavoogudel alata kas perioodi lõpus või alguses. Erinevalt funktsiooni NPV muutuvatest rahavoogude väärtustest peavad funktsiooni PV rahavood olema püsivad kogu investeeringu jooksul. Teabe saamiseks annuiteetidest ja rahandusfunktsioonidest vt funktsiooni PV.

Näide 1

Järgmises näites:

• Määr on aastane diskontomäär.

• Väärtus1 on ühe aasta pärast tänasest investeeringu algmaksumus.

• Väärtus2 on esimese aasta tulu.

• Väärtus3 on teise aasta tulu.

• Väärtus4 on kolmanda aasta tulu.

Näites kaasate ühe väärtusena algse 10 000 $, kuna makse tehakse esimese perioodi lõpus.

Näide 2

Järgmises näites:

• Määr on aastane diskontomäär. See võib tähistada inflatsioonimäära või võistleva investeeringu intressimäära.

• Väärtus1 on ühe aasta pärast tänasest investeeringu algmaksumus.

• Väärtus2 on esimese aasta tulu.

• Väärtus3 on teise aasta tulu.

• Väärtus4 on kolmanda aasta tulu.

• Väärtus5 on neljanda aasta tulu.

• Väärtus6 on viienda aasta tulu.

Näites ei kaasata algset 40 000 $ maksumust ühena väärtustest, kuna makse toimub esimese perioodi alguses.