NB!: Office 2016 ja Office 2019 kasutajatugi katkestati 14. oktoobril 2025. Võtke kasutusele Microsoft 365, et töötada asukohast ja seadmest olenemata ning saada jätkuvalt tuge. Hankige Microsoft 365
Selles artiklis käsitletakse Microsoft Exceli lisandmooduli Solver kasutamist mõjuanalüüsi jaoks, et määrata kindlaks optimaalne tootevalik.
Kuidas kindlaks teha igakuine tootevalik, mis suurendab kasumlikkust?
Ettevõtted peavad sageli iga toote igakuiseks tootmiseks koguse kindlaks määrama. Kõige lihtsamal kujul hõlmab tootevaliku probleem seda, kuidas määrata kindlaks iga toote kogus, mis tuleks kasumi maksimeerimiseks kuu jooksul toota. Tootesegu peab tavaliselt vastama järgmistele piirangutele:
-
Tootesegu ei saa kasutada rohkem ressursse, kui on saadaval.
-
Iga toote järele on piiratud nõudlus. Me ei saa kuu jooksul toota rohkem toodet kui nõudlus dikteerib, sest liigne tootmine on raisatud (näiteks riknev ravim).
Lahendame nüüd järgmise tootesegu probleemi näite. Selle probleemi lahenduse leiate joonisel 27–1 kujutatud faili Prodmix.xlsx.
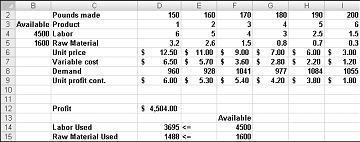
Oletame, et töötame ravimiettevõttes, kes toodab oma ettevõttes kuut erinevat toodet. Iga toote tootmine nõuab tööjõudu ja toorainet. Joonise 27–1 4. reas on näidatud iga toote naela tootmiseks vajalikud töötunnid ja 5. reas on näidatud iga toote naela tootmiseks vajaliku tooraine nael. Näiteks toote 1 naela tootmiseks on vaja kuus tundi tööjõudu ja 3,2 naela toormaterjali. Iga ravimi puhul on hind naela kohta esitatud 6. reas, ühiku maksumus naela kohta on esitatud 7. reas ja kasumiosalus naela kohta on esitatud 9. reas. Näiteks müüb Toode 2 11,00 eurot naela kohta, ühiku hind on 5,70 eurot naela kohta ja annab 5,30 eurot kasumit naela kohta. Kuu nõudlus iga ravimi järele on esitatud 8. reas. Näiteks toote 3 nõudlus on 1041 naela. Sel kuul on saadaval 4500 tundi tööjõudu ja 1600 naela toormaterjali. Kuidas saab see ettevõte maksimeerida oma igakuist kasumit?
Kui me Exceli Solverist midagi ei teadnud, siis ründaksime seda probleemi, koostades töölehe, et jälgida tootevalikuga seotud kasumit ja ressursikasutust. Siis kasutaksime prooviversiooni ja viga selleks, et muuta tootevalikut kasumi optimeerimiseks, ilma et kasutataks rohkem tööjõudu või toorainet, kui see on saadaval, ja tootmata mis tahes ravimit, mis ületab nõudlust. Solverit kasutatakse selles protsessis ainult proovi- ja veaetapis. Sisuliselt on Solver optimeerimismootor, mis sooritab vigase otsingu proovi- ja tõrkeotsingul.
Tootevaliku probleemi lahendamisel on oluline arvutada tõhusalt iga tootevalikuga seotud ressursikasutus ja kasum. Oluline tööriist, mida saame selle arvutuse tegemiseks kasutada, on SUMPRODUCT funktsioon. Funktsioon SUMPRODUCT korrutab vastavad väärtused lahtrivahemikes ja tagastab nende väärtuste summa. Igal SUMPRODUCT väärtustataval lahtrivahemikul peavad olema samad mõõtmed, mis tähendab, et SUMPRODUCT saab kasutada kahe rea või kahe veeruga, kuid mitte ühe veeru ja ühe reaga.
Näitena selle kohta, kuidas saame tootevaliku näites kasutada funktsiooni SUMPRODUCT, proovime arvutada ressursikasutust. Meie tööjõukasutust arvutab
(Töö, mida kasutatakse ravimi naela kohta 1)*(Toodetud ravim 1 nael)+ (Töö, mida kasutatakse ravimi naela kohta 2)*(Toodetud ravim 2 naela) + ... (Töö, mida kasutatakse raviminael 6)*(Toodetud 6 naelaga ravim)
Tööjõukasutus võib tüütumalt arvutada kui D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Samamoodi võib tooraine kasutamise arvutada kujul D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Kuid nende valemite sisestamine kuue toote töölehele on aeganõudev. Kujutage ette, kui kaua aega kuluks, kui töötaksite ettevõttega, kes toodab nende tehases näiteks 50 toodet. Palju lihtsam viis tööjõu ja toorainekasutuse arvutamiseks on kopeerida D14-st D15-sse valem SUMPRODUCT($D$2:$I$2,D4:I4). See valem arvutab D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (mis on meie tööjõukasutus), kuid seda on palju lihtsam sisestada! Pange tähele, et ma kasutan $ märk vahemik D2:I2 nii, et kui ma kopeerin valemi ma ikka jäädvustada toote segu reas 2. Lahtris D15 olev valem arvutab tooraine kasutamise.
Sarnasel moel määrab meie kasum
(Narkootikum 1 kasum naela kohta)*(Toodetud ravim 1 nael) + (Narkootikum 2 kasumit naela kohta)*(Toodetud ravim 2 naela) + ... (Narkootikum 6 kasumit naela kohta)*(Toodetud 6 naelaga ravim 6 naela)
Kasum arvutatakse lahtris D12 hõlpsalt valemiga SUMPRODUCT(D9:I9,$D$2:$I$2).
Nüüd saame tuvastada meie tootesegu Solveri mudeli kolm komponenti.
-
Sihtlahter. Meie eesmärk on maksimeerida kasumit (arvutatud lahtris D12).
-
Lahtrite muutmine. Iga toote toodetud naelade arv (loetletud lahtrivahemikus D2:I2)
-
Piirangud. Meil on järgmised piirangud.
-
Ärge kasutage rohkem tööjõudu ega toorainet, kui on saadaval. St lahtrites D14:D15 (kasutatavad ressursid) olevad väärtused peavad olema väiksemad või võrdsed lahtrites F14:F15 olevate väärtustega (saadaolevad ressursid).
-
Ärge tootke rohkem ravimit kui on nõudlus. See st rakkude D2:I2 (iga ravimi toodetud nael) väärtused peavad olema väiksemad või võrdsed iga ravimi nõudlusega (loetletud lahtrites D8:I8).
-
Me ei saa toota negatiivset kogust narkootikume.
-
Näitan teile, kuidas siseneda sihtlahtrisse, muuta lahtreid ja kitsendusi Solverisse. Seejärel peate vaid klõpsama nuppu Lahenda, et leida kasumit suurendav tootevalik!
Alustamiseks klõpsake menüü Andmed jaotises Analüüs nuppu Solver.
Märkus.: Nagu on selgitatud 26. peatükis "Exceli Solveriga optimeerimise tutvustus", installitakse Solver, klõpsates Microsoft Office'i nuppu ja seejärel nuppu Exceli suvandid ning seejärel lisandmoodleid. Klõpsake loendis Haldamine väärtust Exceli lisandmoodulid, märkige ruut Solveri lisandmoodum ja seejärel klõpsake nuppu OK.
Kuvatakse dialoogiboks Solveri parameetrid, nagu on näidatud joonisel 27–2.
Klõpsake välja Määra sihtlahter ja seejärel valige meie kasumilahter (lahter D12). Klõpsake välja Lahtrite muutmise teel ja seejärel osutage vahemikule D2:I2, mis sisaldab iga ravimi toodetud naelte. Dialoogiboks peaks nüüd välja nägema joonis 27–3.
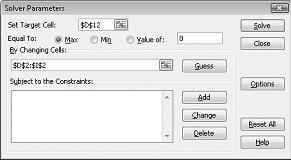
Nüüd oleme valmis mudelile piiranguid lisama. Klõpsake nuppu Lisa. Kuvatakse dialoogiboks Piirangu lisamine joonisel 27–4.
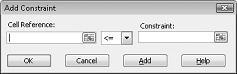
Ressursikasutuse piirangute lisamiseks klõpsake välja Lahtriviide ja valige vahemik D14:D15. Valige keskmisest loendist <=. Klõpsake välja Piirang ja seejärel valige lahtrivahemik F14:F15. Dialoogiboks Lisa piirang peaks nüüd välja nägema selline, nagu joonis 27–5.
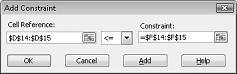
Nüüd oleme taganud, et kui Solver proovib muutuvate lahtrite jaoks erinevaid väärtusi, kaalutakse ainult neid kombinatsioone, mis vastavad nii D14<=F14 (kasutatav tööjõud on vabast tööjõust väiksem või sellega võrdne) ja D15<=F15 (kasutatav tooraine on saadaolevast toorainest väiksem või sellega võrdne). Nõudluse piirangute sisestamiseks klõpsake nuppu Lisa. Täitke dialoogiboksi Piirangu lisamine, nagu on näidatud joonisel 27–6.
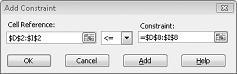
Nende piirangute lisamine tagab, et kui Solver proovib muutuvate lahtriväärtuste jaoks erinevaid kombinatsioone, võetakse arvesse ainult järgmisi parameetreid rahuldavaid kombinatsioone:
-
D2<=D8 (Drug 1 toodetud kogus on väiksem või võrdne nõudlusega Drug 1 järele)
-
E2<=E8 (Drug 2 toodetud kogus on väiksem või võrdne nõudlusega Drug 2 järele)
-
F2<=F8 (ravimi 3 toodetud kogus on väiksem või võrdne nõudlus drug 3 järele)
-
G2<=G8 (ravimi 4 toodetud kogus on väiksem või võrdne nõudlusega Drug 4 järele)
-
H2<=H8 (ravimi 5 toodetud kogus on väiksem või võrdne nõudlusega Drug 5 järele)
-
I2<=I8 (uimasti 6 toodetud kogus on väiksem või võrdne nõudlusega Drug 6 järele)
Klõpsake dialoogiboksis Piirangu lisamine nuppu OK. Solveri aken peaks välja nägema selline, nagu joonis 27–7.
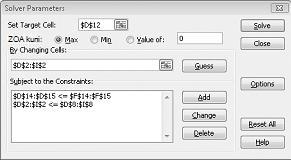
Dialoogiboksis Solveri suvandid sisestame piirangu, et lahtrite muutmine ei tohi olla negatiivne. Klõpsake dialoogiboksis Solveri parameetrid nuppu Suvandid. Märkige ruudud Eelda lineaarset mudelit ja Eelda mittenegatiivset, nagu on näidatud järgmisel lehel joonisel 27–8. Klõpsake nuppu OK.
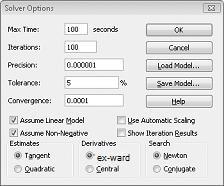
Ruudu Eelda mittenegatiivset märkimine tagab, et Solver arvestab ainult muutuvate lahtrite kombinatsioone, kus iga muutuv lahter eeldab mittenegatiivset väärtust. Kontrollisime välja Eelda lineaarset mudelit, kuna tootesegu probleem on eritüüp Solveri probleem, mida nimetatakse lineaarseks mudeliks. Solveri mudel on lineaarne järgmistel tingimustel.
-
Sihtlahtri arvutamiseks liidetakse kokku vormi terminid (muutuvad lahtrid)*(konstant).
-
Iga piirang vastab "lineaarse mudeli nõudele". See tähendab, et iga kitsendust hinnatakse, liites kokku vormi terminid (muutes lahtrit)*(konstanti) ja võrdledes summasid konstandiga.
Miks on see Solveri probleem lineaarne? Meie sihtlahter (kasum) arvutatakse kui
(Narkootikum 1 kasum naela kohta)*(Toodetud ravim 1 nael) + (Narkootikum 2 kasumit naela kohta)*(Toodetud ravim 2 naela) + ... (Narkootikum 6 kasumit naela kohta)*(Toodetud 6 naelaga ravim 6 naela)
See arvutus järgib mustrit, milles sihtlahtri väärtus tuletatakse, liites kokku vormi terminid (muutes lahtrit)*(konstant).
Meie tööjõupiirangut hinnatakse, võrreldes väärtust, mis on tuletatud (Ravimi 1 naela kohta kasutatud tööjõud)*(Toodetud ravim 1 naela) + (Tööjõu kasutamine nael narkootikumi 2 kohta)*(Toodetud narkootikumide 2 naela)+ ... (Töö meided naela kohta Narkootikum 6)*(Toodetakse 6 naela) tööjõule.
Seetõttu hinnatakse tööpiirangut, liites kokku vormi terminid (muutes lahtrit)*(konstant) ja võrdledes summasid konstandiga. Nii tööjõu piirang kui ka tooraine piirang vastavad lineaarse mudeli nõudele.
Meie nõudmise piirangud on vormil
(Ravim 1 toodetud)<=(Drug 1 Demand) (Drug 2 produced)<=(Drug 2 Demand) §(Drug 6 produced)<=(Drug 6 Demand)
Iga nõudluse piirang vastab ka lineaarse mudeli nõudele, kuna iga väärtustatakse, liites kokku vormi tingimused (muutes lahtrit)*(konstant) ja võrdledes summasid konstandiga.
Kas oleme näidanud, et meie tootevalikumudel on lineaarne mudel, miks peaksime hoolima?
-
Kui Solveri mudel on lineaarne ja valime Eelda lineaarset mudelit, on Solveril tagatud Solveri mudeli optimaalse lahenduse leidmine. Kui Solveri mudel pole lineaarne, võib Solver optimaalse lahenduse leida või mitte.
-
Kui Solveri mudel on lineaarne ja valime Eelda lineaarset mudelit, kasutab Solver mudeli optimaalse lahenduse leidmiseks väga tõhusat algoritmi (simplex-meetodit). Kui Solveri mudel on lineaarne ja me ei vali käsku Eelda lineaarset mudelit, kasutab Solver väga ebaefektiivset algoritmi (GRG2-meetodit) ja võib mudeli optimaalse lahenduse leidmisel tekkida raskusi.
Pärast dialoogiboksis Solveri suvandid nupu OK klõpsamist naaseme põhidialoogiboksi Solver, mis on kuvatud joonisel 27–7 eespool. Nupu Lahenda klõpsamisel arvutab Solver meie tootesegumudeli jaoks optimaalse lahenduse (kui see on olemas). Nagu ma 26. Jällegi on teostatav lahendus kõigile piirangutele vastavate muutuvate lahtriväärtuste kogum. Joonisel 27–9 kuvatavad muutuvad lahtriväärtused on teostatav lahendus, kuna kõik tootmistasemed on mittenegatiivsed, tootmistasemed ei ületa nõudlust ja ressursikasutus ei ületa saadaolevaid ressursse.
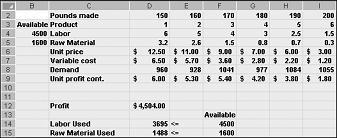
Järgmisel lehel joonisel 27–10 kuvatud muutuvad lahtriväärtused tähistavad sobimatut lahendust järgmistel põhjustel.
-
Me toodame rohkem Drug 5 kui nõudlus selle järele.
-
Kasutame saadaolevast rohkem tööjõudu.
-
Kasutame rohkem toormaterjali kui on saadaval.
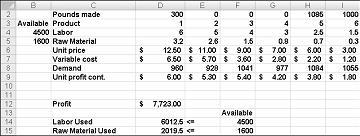
Pärast nupu Lahenda klõpsamist leiab Solver kiiresti joonisel 27–11 näidatud optimaalse lahenduse. Töölehel optimaalsete lahenduseväärtuste säilitamiseks peate valima Käsu Säilita Solveri lahendus.
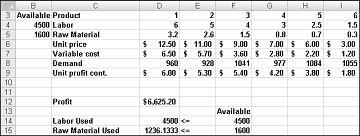
Meie ravimifirma saab oma igakuise kasumi maksimeerida 6625,20 dollari tasemel, luues 596,67 naela Drug 4, 1084 naela Drug 5 ja mitte ühtegi teist ravimit! Me ei saa muudel viisidel kindlaks teha, kas saame maksimaalset kasumit 6625,20 $. Saame olla kindlad vaid selles, et piiratud ressursside ja nõudlusega ei saa me sel kuul teha rohkem kui 6627.20 dollarit.
Oletagem, et iga toote nõudlus peab olema täidetud. (Vt faili Prodmix.xlsx töölehte Võimaliku lahenduseta .) Seejärel peame muutma oma nõudluse piirangud vahemikusT D2:I2<=D8:I8 kuni D2:I2>=D8:I8. Selleks avage Solver, valige kitsendus D2:I2<=D8:I8 ja seejärel klõpsake nuppu Muuda. Kuvatakse dialoogiboks Piirangu muutmine joonistel 27–12.
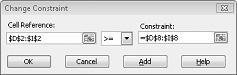
Valige >=ja seejärel klõpsake nuppu OK. Nüüd oleme taganud, et Solver kaalub ainult kõigile nõudmistele vastavate lahtriväärtuste muutmist. Nupu Lahenda klõpsamisel kuvatakse teade "Solver ei leidnud sobivat lahendust". See sõnum ei tähenda, et tegime oma mudelis vea, vaid et oma piiratud ressurssidega ei suuda me rahuldada nõudlust kõigi toodete järele. Solver ütleb meile lihtsalt, et kui me tahame rahuldada iga toote nõudlust, peame lisama rohkem tööjõudu, rohkem tooraineid või rohkem mõlemaid.
Vaatame, mis juhtub, kui lubame iga toote jaoks piiramatut nõudlust ja me lubame iga ravimi negatiivseid koguseid. (See Solveri probleem kuvatakse faili Prodmix.xlsx töölehel Väärtuste seadmine ära koondu .) Selle olukorra jaoks optimaalse lahenduse leidmiseks avage Solver, klõpsake nuppu Suvandid ja tühjendage ruut Eelda mittenegatiivset. Valige dialoogiboksis Solveri parameetrid nõudluse piirang D2:I2<=D8:I8 ja seejärel klõpsake piirangu eemaldamiseks nuppu Kustuta. Nupu Lahenda klõpsamisel tagastab Solver teate "Määra lahtriväärtused ära koondu". See teade tähendab, et kui sihtlahter tuleb maksimeerida (nagu meie näites), on võimalikud lahendused meelevaldselt suurte sihtlahtriväärtustega. (Kui sihtlahter tuleb minimeerida, tähendab teade "Sea lahtriväärtused ära koondu" meelevaldselt väikeste sihtlahtriväärtuste puhul mõistlikke lahendusi.) Meie olukorras, lubades ravimi negatiivset tootmist, loome me tegelikult ressursse, mida saab kasutada meelevaldselt suure hulga muude ravimite tootmiseks. Arvestades meie piiramatut nõudlust, võimaldab see meil teenida piiramatut kasumit. Reaalses olukorras ei saa me teha lõpmatut summat raha. Lühidalt, kui kuvatakse tekst "Set Values Do Not Converge" (Määra väärtused ei koondu), on teie mudelil tõrge.
-
Oletame, et meie ravimifirma saab osta kuni 500 tundi tööjõudu hinnaga $1 rohkem tunnis kui jooksvad tööjõukulud. Kuidas me saame kasumit maksimeerida?
-
Kiibitootmisettevõttes toodavad neli tehnikut (A, B, C ja D) kolme toodet (tooted 1, 2 ja 3). Sel kuul saab kiibi tootja müüa 80 tooteühikut Product 1, 50 toote 2 ühikut ja kuni 50 tooteühikut tootest Product 3. Tehnik A saab teha ainult tooteid 1 ja 3. Tehnik B saab teha ainult tooteid 1 ja 2. Tehnik C saab teha ainult toodet Product 3. Tehnik D saab teha ainult toodet Product 2. Iga toodetud ühiku kohta annavad tooted järgmise kasumi: Toode 1, 6 $; Toode 2, $7; ja Product 3, $10. Aeg (tundides), mille jooksul iga tehnik peab toodet valmistama, on järgmine:
Toode
Tehnik A
Tehnik B
Tehnik C
Tehnik D
1
2
2,5
Ei saa teha
Ei saa teha
2
Ei saa teha
3
Ei saa teha
3,5
3
3
Ei saa teha
4
Ei saa teha
-
Iga tehnik saab töötada kuni 120 tundi kuus. Kuidas saab kiibi tootja maksimeerida oma igakuist kasumit? Oletagem, et toota saab murdarvu ühikuid.
-
Arvutitootmisettevõte toodab hiiri, klaviatuure ja videomängude juhtkangi. Ühikupõhine kasum, ühikupõhine tööjõukasutus, igakuine nõudlus ja ühikupõhine masinaaja kasutamine on esitatud järgmises tabelis:
Hiired
Klaviatuurid
Juhtkangid
Kasum/ühik
8 $
11 $
9 $
Töökasutus/-üksus
.2 tund
0,3 tundi
0,24 tundi
Seadme aeg/ühik
.04 tund
055 tundi
.04 tund
Igakuine nõudlus
15 000
27,000
11,000
-
Igal kuul on saadaval kokku 13 000 tööaega ja 3000 tundi masinaaega. Kuidas saab tootja oma igakuise kasumiosaluse maksimeerida?
-
Lahendage meie narkootikumide näide eeldusel, et iga ravimi minimaalne nõudlus on 200 ühikut.
-
Jason valmistab rombist käevõrusid, kaelakeesid ja kõrvarõngaid. Ta tahab töötada maksimaalselt 160 tundi kuus. Tal on 800 untsi teemante. Allpool on esitatud teemantide kasum, tööaeg ja iga toote tootmiseks vajalikud untsid. Kui nõudlus iga toote järele on piiramatu, kuidas saab Jason oma kasumit maksimeerida?
Toode
Ühiku kasum
Töötunnid ühiku kohta
Rombid ühiku kohta
Käevõru
300 €
.35
1,2
Kaelakee
200 €
.15
.75
Kõrvarõngad
100 €
0,05
.5










