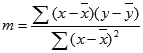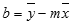Tässä artikkelissa kuvataan Microsoft Excelin LINREGR-funktion kaavasyntaksi ja käyttö.
Kuvaus
LINREGR-funktio laskee tilastotiedot tietoihin parhaiten sopivalle suoralle käyttäen pienimmän neliön menetelmää ja palauttaa sitten suoraa kuvaavan matriisin. Voit myös yhdistää LINREGR-funktion muihin funktioihin, kun haluat laskea tilastoja muuntyyppisille malleille, joiden tuntemattomat parametrit ovat lineaarisia, mukaan lukien polynomiset, logaritmiset ja eksponentiaaliset sarjat sekä potenssisarjat. Koska tämä funktio palauttaa arvomatriisin, funktio on kirjoitettava matriisikaavana. Ohjeet noudattavat tässä artikkelissa olevia esimerkkejä.
Suoran yhtälö on
y = mx + b
tai
y = m1x1 + m2x2 + ... + b
jos on useita x-arvoja, joissa riippuvat y-arvot ovat riippumattomien x-arvojen funktio. M-arvot ovat riippumattomien x-arvojen kertoimia, ja b on vakioarvo. Huomaa, että y, x ja m voivat olla vektoreita. Funktion LINREGR palauttama matriisi on {mn;mn-1;...;m1;b}. LINREGR voi palauttaa myös muita regressiota kuvaavia tietoja.
Syntaksi
LINREGR(tunnettu_y; [tunnettu_x]; [vakio]; [tilasto])
LINREGR-funktion syntaksissa on seuraavat argumentit:
known_y Pakollinen. Y-arvojen joukko, joka tunnetaan kaavasta y = mx + b.
- Jos known_y-alue on yhdessä sarakkeessa, jokainen known_x sarake tulkitaan erillisenä muuttujana.
- Jos known_y alue sisältyy yhteen riviin, jokainen known_x rivi tulkitaan erilliseksi muuttujaksi.
known_x Valinnainen. X-arvojen joukko, joka jo mahdollisesti tunnetaan kaavasta y = mx + b.
- known_x alue voi sisältää yhden tai usean muuttujajoukon. Jos käytetään vain yhtä muuttujaa, known_y ja known_x voivat olla minkä tahansa muotoisia alueita, kunhan niiden ulottuvuus on sama. Jos muuttujia on useita, known_y on oltava vektori (eli alue, jonka korkeus on yksi rivi tai jonka leveys on yksi sarake).
- Jos known_x jätetään pois, sen oletetaan olevan matriisi {1,2,3,...}, joka on yhtä suuri kuin known_y.
const Valinnainen. Totuusarvo, joka määrittää, onko vakion b oltava yhtä suuri kuin 0.
- Jos vakio-argumentti on TOSI tai se puuttuu, b lasketaan normaalisti.
- Jos vakio-argumentti on EPÄTOSI, b:n arvoksi määritetään 0 ja m-arvot sovitetaan sovittamaan y = mx.
Tilastot Valinnainen. Totuusarvo, joka määrittää, palauttaako ohjelma muita regressiota koskevia tietoja.
- Jos tilasto on TOSI, LINREGR palauttaa regressiota koskevia lisätietoja. Tällöin palautettu matriisi on {mn;mn-1,...,m1;b; sen,sen-1,...,se1,seb; r2,sey; F,df; ssreg,ssresid}.
- Jos tilasto on EPÄTOSI tai se puuttuu, LINREGR palauttaa vain kertoimien m ja vakion b arvot.
Regressiota koskevat lisätiedot ovat seuraavat:
| Tieto: | Kuvaus |
|---|---|
| se1;se2;...;sen | Kertoimien m1;m2;...;mn keskivirheet. |
| seb | Vakion b keskivirhe (seb = #N/A, kun vakio on EPÄTOSI). |
| R2 | Determinaatiokerroin. Vertaa arvioituja ja todellisia y-arvoja ja arvoalueita 0–1. Jos se on 1, otoksessa on täydellinen korrelaatio – arvioidun y-arvon ja todellisen y-arvon välillä ei ole eroa. Jos determinaatiokerroin on 0, regressioyhtälöstä ei ole apua y-arvon ennustamisessa. Lisätietoja arvon2 laskemisesta on tämän ohjeaiheen Huomautuksia-osassa. |
| sey | Arvioidun y-arvon keskivirhe. |
| täydellinen | Vaikutusten merkitsevyys. F-arvojen avulla voit määrittää, johtuuko riippumattomien ja riippuvien muuttujien ja selittäjien välinen korrelaatio vain sattumasta. |
| df | Vapausasteet. Vapausasteiden avulla löydetään F-arvoissa käytettävät merkitsevyysrajat taulukkokirjojen taulukosta. Määritä mallin luottamustaso vertaamalla taulukon F-arvoja LINREGR-funktion palauttamiin arvoihin. Tietoja vapausasteiden laskemisesta on tämän ohjeaiheen Huomautuksia-osassa. Esimerkissä 4 on esitetty F:n ja df:n käyttö. |
| ssreg | Kokonaisneliösumma. |
| ssresid | Jäännösneliösumma. Tietoja ssreg- ja ssresid-arvojen laskemisesta on tämän ohjeaiheen Huomautuksia-osassa. |
Alla on esitetty järjestys, jossa funktio palauttaa regression lisätiedot.
Huomautuksia
Voit määrittää minkä tahansa suoran antamalla sen kulmakertoimen ja y-akselin leikkauspisteen:
Kaltevuus (m):
Jos haluat löytää suoran kulmakertoimen, joka kirjoitetaan usein m:llä, ota suoralta kaksi pistettä (x1,y1) ja (x2,y2); Kulmakerroin on (y2-y1)/(x2-x1).
Y-akselin leikkauspiste (b):
y-akselin leikkauspiste, jota merkitään yleensä parametrilla b, on y:n arvo pisteessä, jossa suora leikkaa y-akselin.
Suoran yhtälö on y = mx + b. Kun tunnet m:n ja b:n arvot, voit laskea minkä tahansa suoralla olevan pisteen arvon käyttämällä yhtälössä y:n tai x:n arvoa. Voit käyttää myös SUUNTAUS-funktiota.Jos käytettävissä on vain yksi riippumaton x-muuttuja, voit laskea kulmakertoimen ja y-akselin leikkauspisteen suoraan seuraavien kaavojen avulla:
Kaltevuus:
=INDEKSI(LINREGR(known_y's;known_x's);1)
Y-akselin leikkauspiste:
=INDEKSI(LINREGR(known_y's;known_x's);2)LINREGR-funktiolla laskettu suoran tarkkuus riippuu tietojen hajonnasta. Mitä lineaarisemmat tiedot ovat, sitä tarkempi on LINREGR-funktion malli. LINREGR-funktio sovittaa tiedot pienimmän neliösumman menetelmän avulla. Jos käytät vain yhtä riippumatonta x-muuttujaa, m:n ja b:n arvojen laskeminen perustuu seuraaviin kaavoihin:
jossa x ja y ovat otosten keskiarvoja; eli x = KESKIARVO(tunnettu x) ja y = KESKIARVO(known_y).Suoran ja käyrän sovitusfunktiot LINREGR ja LOGREGR laskevat tietoihin parhaiten sopivan suoran tai eksponenttikäyrän. Sinun täytyy kuitenkin valita, kumpi kahdesta tuloksesta sopii parhaiten tietoihin. Voit laskea funktion TREND(known_y's,known_x's) suoralle viivalle ja KASVU(known_y's, known_x's) eksponentiaalikäyrälle. Nämä funktiot palauttavat ilman new_x argumenttia y-arvomatriisin, joka on ennustettu kyseisen suoran tai käyrän mukaan todellisiin arvopisteisiin. Sen jälkeen voit verrata laskettuja arvoja todellisiin arvoihin. Vertailu on helpompaa, jos esität molemmat arvosarjat kaaviona.
Regressioanalyysissa Excel laskee kullekin pisteelle arvioidun y-arvon ja sen todellisen y-arvon erotuksen. Näiden neliöerotusten summaa kutsutaan neliöiden jäännössummaksi (ssresid). Excel laskee sitten neliöiden kokonaissumman, sstotal. Kun vakioargumentti = TOSI tai se puuttuu, neliösummien kokonaissumma on todellisten y-arvojen ja y-arvojen keskiarvon välisten neliöerotusten summa. Kun vakioargumentti = FALSE, neliösummien kokonaissumma on todellisten y-arvojen neliöiden summa (vähentämättä keskimääräistä y-arvoa kustakin yksittäisestä y-arvosta). Sitten regression sum of squares, ssreg, voidaan löytää osoitteesta: ssreg = sstotal - ssresid. Mitä pienempi neliöiden jäännössumma on neliöiden kokonaissummaan verrattuna, sitä suurempi on determinaatiokertoimen arvo r2, joka osoittaa, kuinka hyvin regressioanalyysin tuloksena syntyvä yhtälö selittää muuttujien välisen suhteen. Arvor 2 on yhtä suuri kuin ssreg/sstotal.
Joissakin tapauksissa yksi tai useampi x-sarake (oletetaan, että y:n ja x:n arvot ovat sarakkeissa) ei vaikuta muiden x-sarakkeiden kanssa tehtävään ennusteeseen. Toisin sanoen yhden tai useamman x-sarakkeen poistaminen ei vaikuta ennustettujen y-arvojen tarkkuuteen. Tällaisessa tapauksessa nämä redundantit x-sarakkeet tulee jättää pois regressiomallista. Tätä ilmiötä kutsutaan "kolineaarisuudeksi", koska minkä tahansa redundantin x-sarakkeen voi ilmaista muiden, vaikuttavien sarakkeiden monikertojen summana. LINREGR-funktio tarkistaa kolineaarisuuden ja poistaa mahdolliset redundantit x-sarakkeet regressiomallista havaittuaan ne. Poistetut x-sarakkeet tunnistaa LINREGR-tulosteessa siitä, että niillä on 0 kerrointa ja 0 se-arvoa. Jos yksi tai useampi sarake poistetaan redundanttina, df-arvo muuttuu, sillä df-arvoon vaikuttaa ennusteessa varsinaisesti käytettyjen x-sarakkeiden määrä. Lisätietoja df:n laskemisesta on seuraavassa esimerkissä 4. Jos df muuttuu redundanttien x-sarakkeiden poistamisen seurauksena, myös sey- ja F-arvot muuttuvat. Kolineaarisuuden pitäisi olla käytännössä suhteellisen harvinaista. Yhdessä tapauksessa on kuitenkin tavallista todennäköisempää, että joissakin x-sarakkeissa on vain 0- ja 1-arvoja ilmaisemassa, onko kokeen kohde tietyn ryhmän jäsen vai ei. Jos vakio = TOSI tai se jätetään pois, LINREGR-funktio mallintaa leikkauspisteen lisäämällä ylimääräisen x-sarakkeen kaikista 1-arvoista. Jos yhdessä sarakkeessa kaikkien miespuolisten kohteiden arvo on 1 ja naispuolisten 0 ja toisessa sarakkeessa puolestaan kaikkien naispuolisten kohteiden arvo on 1 ja miespuolisten 0, jälkimmäinen sarake on redundantti, koska sen arvot voidaan saada vähentämällä miessarakkeen arvot ylimääräisestä LINREGR-funktion lisäämästä pelkästään 1-arvoja sisältävästä sarakkeesta.
Df:n arvo lasketaan seuraavasti, kun yhtään x-saraketta ei poisteta mallista kolineaarisuuden vuoksi: jos known_x-sarakkeitaon k ja vakio = TOSI tai jätetään pois, df = n – k – 1. Jos vakio = EPÄTOSI, df = n - k. Molemmissa tapauksissa kukin kolineaarisuuden vuoksi poistettu x-sarake lisää df-arvoa yhdellä.
Jos kirjoitat argumentiksi matriisivakion, kuten known_x:n), erota samalla rivillä olevat arvot puolipisteillä ja erota rivit kenoviivalla. Erotinmerkit voivat olla eri merkkejä aluekohtaisten asetusten mukaan.
Huomaa, että regressioyhtälöllä ennustetut y-arvot eivät ehkä ole kelvollisia, jos ne ovat yhtälön määrityksessä käytetyn y-arvojen alueen ulkopuolella.
LINREGR-funktiossa käytetty algoritmi on erilainen kuin KULMAKERROIN- ja LEIKKAUSPISTE-funktioissa käytetty algoritmi. Näiden algoritmien väliset erot voivat johtaa erilaisiin tuloksiin, kun tiedot ovat määrittämättömiä ja samansuuntaisia. Jos esimerkiksi known_y argumentin arvopisteet ovat nollia ja known_x argumentin arvopisteet ovat ykkösiä:
- LINREGR palauttaa arvon 0. LINREGR-funktion algoritmi on suunniteltu palauttamaan kohtuullisia tuloksia myös samansuuntaisista tiedoista, ja tässä tapauksessa se löytää ainakin yhden vastauksen.
- KULMAKERROIN- ja LEIKKAUSPISTE palauttavat #JAKO/0! -virheen. KULMAKERROIN- ja LEIKKAUSPISTE-funktioiden algoritmit on suunniteltu etsimään vain yhden vastauksen, ja tällaisessa tapauksessa vastauksia voi olla useita.
Sen lisäksi, että lasket tilastoja muista regressiotyypeistä LOGREGR-funktiolla, voit LINREGR-funktiolla laskea erilaisia regressiotyyppejä kirjoittamalla x- ja y-muuttujien funktiot x- ja y-sarjoina LINREGR-funktiolle. Esimerkiksi seuraava kaava:
=LINREGR(yarvot, xarvot^SARAKE($A:$C))
toimii, kun käytössä on yksi y-arvosarake ja yksi x-arvosarake seuraavan kolmannen asteen yhtälön likiarvon laskemista varten:
y = m1*x + m2*x^2 + m3*x^3 + b
Voit tätä kaavaa muuttamalla laskea myös muuntyyppisiä regressioita, mutta joissakin tapauksissa on muutettava tulostusarvoja ja muita tilastoja.LINREGR-funktion palauttama F-testiarvo on eri kuin FTESTI-funktion palauttama arvo. LINREGR palauttaa F-jakauman, mutta FTESTI palauttaa todennäköisyysarvon.
Esimerkkejä
Esimerkki 1 - Kulmakerroin ja y-akselin leikkauspiste
Kopioi esimerkkitiedot seuraavaan taulukkoon ja lisää se uuden Excel-laskentataulukon soluun A1. Kaavat näyttävät tuloksia, kun valitset ne, painat F2-näppäintä ja sitten Enter-näppäintä. Voit säätää sarakkeiden leveyttä, että näet kaikki tiedot.
| Tunnettu y | Tunnettu x |
|---|---|
| 1 | 0 |
| 9 | 4 |
| 5 | 2 |
| 7 | 3 |
| Tulos (kulmakerroin) | Tulos (y-leikkauspiste) |
| 2 | 1 |
| Kaava (matriisikaava soluissa A7:B7) | |
| =LINREGR(A2:A5;B2:B5;;EPÄTOSI) |
Esimerkki 2 - Yhden muuttujan lineaarinen regressio
Kopioi esimerkkitiedot seuraavaan taulukkoon ja lisää se uuden Excel-laskentataulukon soluun A1. Kaavat näyttävät tuloksia, kun valitset ne, painat F2-näppäintä ja sitten Enter-näppäintä. Voit säätää sarakkeiden leveyttä, että näet kaikki tiedot.
| Kuukausi | Myynti |
|---|---|
| 1 | 3 100 € |
| 2 | 4 500 € |
| 3 | 4 400 € |
| 4 | 5 400 € |
| 5 | 7 500 € |
| 6 | 8 100 € |
| Kaava | Tulos |
| =SUMMA(LINREGR(B1:B6, A1:A6)*{9,1}) | 11 000 € |
| Laskee yhdeksännen kuukauden myyntiarvion kuukausien 1–6 myyntien perusteella. |
Esimerkki 3 - Usean muuttujan lineaarinen regressio
Kopioi esimerkkitiedot seuraavaan taulukkoon ja lisää se uuden Excel-laskentataulukon soluun A1. Kaavat näyttävät tuloksia, kun valitset ne, painat F2-näppäintä ja sitten Enter-näppäintä. Voit säätää sarakkeiden leveyttä, että näet kaikki tiedot.
| Lattiapinta-ala (x1) | Toimistojen määrä (x2) | Sisäänkäynnit (x3) | Ikä (x4) | Arvioitu arvo (y) |
|---|---|---|---|---|
| 2310 | 2 | 2 | 20 | 142 000 € |
| 2333 | 2 | 2 | 12 | 144 000 € |
| 2356 | 3 | 1,5 | 33 | 151 000 € |
| 2379 | 3 | 2 | 43 | 150 000 € |
| 2402 | 2 | 3 | 53 | 139 000 € |
| 2425 | 4 | 2 | 23 | 169 000 € |
| 2448 | 2 | 1,5 | 99 | 126 000 € |
| 2471 | 2 | 2 | 34 | 142 900 € |
| 2494 | 3 | 3 | 23 | 163 000 € |
| 2517 | 4 | 4 | 55 | 169 000 € |
| 2540 | 2 | 3 | 22 | 149 000 € |
| -234,2371645 | ||||
| 13,26801148 | ||||
| 0,996747993 | ||||
| 459,7536742 | ||||
| 1732393319 | ||||
| Kaava (soluun A19 kirjoitettu dynaaminen matriisikaava) | ||||
| =LINREGR(E2:E12;A2:D12;TOSI;TOSI) |
Esimerkki 4 - F- ja r2 -tilastojen käyttäminen
Edellisessä esimerkissä determinaatiokerroin r2 on 0,99675 (katso LINREGR-funktion tuloksen solu A17), mikä osoittaa, että riippumattomien muuttujien ja myyntihinnan välillä on vahva yhteys. F-arvojen avulla voit määrittää, ovatko nämä tulokset syntyneet sattumalta, kun arvo on näin korkea.
Oletetaan, että muuttujien välillä ei ole riippuvuutta mutta että olet onnistunut poimimaan 11 toimistorakennuksen otoksen, jolle regressioanalyysi sattumalta saa suuren korrelaation. Riskitasoksi (alfa) kutsutaan sitä todennäköisyyttä, että päättelet virheellisesti korrelaation olevan olemassa.
LINREGR-funktion tulosteen F- ja df-arvojen avulla voi laskea todennäköisyyden, jolla korkeampi F-arvo syntyy sattumalta. Voit joko verrata F:n arvoa F-jakaumataulukoiden kriittisiin arvoihin tai voit laskea korkeamman F-arvon sattumanvaraisen syntymisen todennäköisyyden Excelin FJAKAUMA-funktion avulla. Oikean F-jakauman vapausasteiden määrät ovat v1 ja v2. Jos n on arvopisteiden määrä ja vakio on TOSI tai se jätetään pois, v1 = n - df - 1 ja v2 = df. (Jos vakio = EPÄTOSI, niin v1 = n – df ja v2 = df.) FJAKAUMA-funktio – jonka syntaksi on FJAKAUMA(F,v1,v2) — palauttaa todennäköisyyden, jolla korkeampi F-arvo syntyy sattumalta. Tässä esimerkissä df = 6 (solu B18) ja F = 459,753674 (solu A18).
Jos oletetaan, että alfa = 0,05, v1 = 11 - 6 - 1 = 4 ja v2 = 6, F:n kriittinen arvo on 4,53. Koska F = 459,753674 on paljon suurempi kuin 4,53, on erittäin epätodennäköistä, että näin korkea F:n arvo on syntynyt sattumalta. (Kun alfa = 0,05, hypoteesi, jonka mukaan known_y:n ja known_x:n välillä ei ole yhteyttä, hylätään, kun F ylittää kriittisen tason 4,53.) Voit laskea Excelin FJAKAUMA-funktion avulla todennäköisyyden, jolla näin korkea F-arvo on syntynyt sattumalta. Esimerkiksi FJAKAUMA(459,753674; 4; 6) = 1,37E-7 on erittäin pieni todennäköisyys. Voit päätellä joko katsomalla F-arvon kriittisen tason taulukosta tai käyttämällä Excelin FJAKAUMA-funktiota, että regressioyhtälö on käyttökelpoinen ennustettaessa toimistorakennusten arvoa tällä alueella. Muista, että edellä olevassa kappaleessa laskettujen oikeiden v1:n ja v2:n arvojen käyttäminen on ensiarvoisen tärkeää.
Esimerkki 5 - T-arvojen laskeminen
Toinen hypoteesitesti määrittää, voidaanko esimerkin 3 toimistotalon arvioinnissa käyttää kunkin muuttujan kulmakerrointa. Jos haluat esimerkiksi testata toimistorakennuksen iän tilastollisen merkitsevyyden, jaa -234,24 (iän kulmakerroin) arvolla 13,268 (arvioitu iän kertoimien keskivirhe solussa A15). T-arvo on seuraava:
t = m4 ÷ se4 = -234,24 ÷ 13,268 = -17,7
Jos t:n itseisarvo on tarpeeksi suuri, voidaan päätellä, että kulmakerroin on käyttökelpoinen esimerkin 3 toimistorakennuksen arvon arvioimisessa. Seuraavassa taulukossa on neljän havaitun t-arvon itseisarvot.
Taulukosta käy ilmi, että kaksisuuntaisen t-jakauman rajapiste on 2,447, kun riskitaso alfa on 0,05 ja vapausasteita on 6. Tämän rajapisteen voi selvittää myös Excelin TJAKAUMA.KÄÄNT-funktion avulla. TJAKAUMA.KÄÄNT(0,05;6) = 2,447. Koska t:n absoluuttinen arvo (17,7) on suurempi kuin 2,447, ikä on tärkeä muuttuja toimistorakennuksen arvoa arvioitaessa. Voit testata kaikkien muiden riippumattomien muuttujien tilastollista merkittävyyttä samaan tapaan. Seuraavassa taulukossa on esitetty kunkin riippumattoman muuttujan t-arvot:
| Muuttuja | Laskettu t-arvo: |
|---|---|
| Lattiapinta-ala | 5,1 |
| Toimistojen määrä | 31,3 |
| Sisäänkäyntien määrä | 4,8 |
| Ikä | 17,7 |
Kaikkien näiden arvojen absoluuttinen arvo on suurempi kuin 2,447, joten kaikki regressioyhtälössä käytetyt arvot ovat hyödyllisiä kyseisellä alueella sijaitsevien toimistorakennusten arvon arvioimisessa.