Tärkeää: Office 2016:n ja Office 2019:n tuki päättyi 14. lokakuuta 2025. Päivitä Microsoft 365:een, jotta voit tehdä yhteistyötä missä tahansa laitteessa ja jatkaa tuen vastaanottamista. Osta Microsoft 365
Tässä artikkelissa käsitellään Ratkaisinta, Microsoft Excel -apuohjelmaa, jota voit käyttää entä jos -analyysiin optimaalisen tuotevalikoiman määrittämiseksi.
Miten voin määrittää kuukausittaisen tuotevalikoiman, joka maksimoi kannattavuuden?
Yritysten on usein määritettävä kunkin tuotteen määrä kuukausittain. Yksinkertaisimmassa muodossaan tuotesekoitusongelma liittyy siihen, miten määritetään kunkin tuotteen määrä, joka on tuotettava kuukauden aikana voittojen maksimoimiseksi. Tuotevalikoiman on yleensä noudatettava seuraavia rajoituksia:
-
Tuotevalikoima ei voi käyttää enempää resursseja kuin on käytettävissä.
-
Kullekin tuotteelle on rajallinen kysyntä. Emme voi tuottaa enemmän tuotetta kuukauden aikana kuin kysyntä määrää, koska ylimääräinen tuotanto menee hukkaan (esimerkiksi pilaantuva lääke).
Ratkaistaan nyt seuraava esimerkki tuotesekoitusongelmasta. Löydät ratkaisun tähän ongelmaan Prodmix.xlsx tiedostosta, joka näkyy kuvassa 27-1.
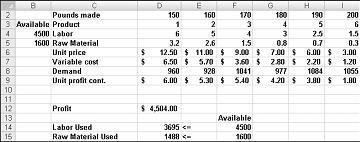
Oletetaan, että työskentelemme lääkeyhtiölle, joka tuottaa kuusi eri tuotetta tehtaallaan. Kunkin tuotteen tuotanto edellyttää työvoimaa ja raaka-ainetta. Kuvan 27–1 rivillä 4 näkyy tuntimäärä, joka tarvitaan kunkin tuotteen kilon tuottamiseen, ja rivillä 5 näytetään raaka-aineen kilot, joita tarvitaan kunkin tuotteen kilon tuottamiseen. Esimerkiksi tuotteen 1 kilon tuottaminen vaatii kuusi tuntia työvoimaa ja 3,2 kiloa raaka-ainetta. Kullekin lääkkeelle hinta puntaa kohti annetaan rivillä 6, yksikkökustannukset paunaa kohti annetaan rivillä 7 ja voitto per punta annetaan rivillä 9. Esimerkiksi Tuote 2 myy hintaan 11,00 $ per punta, sille aiheutuu yksikkökustannukset 5,70 $ per punta ja se tuottaa 5,30 dollarin voiton puntaa kohti. Kuukauden kysyntä kullekin lääkkeelle annetaan rivillä 8. Esimerkiksi tuotteen 3 kysyntä on 1041 paunaa. Tässä kuussa on saatavilla 4500 tuntia työvoimaa ja 1600 kiloa raaka-ainetta. Miten tämä yritys voi maksimoida kuukausittaisen voittonsa?
Jos emme tietäisi mitään ExcelIn ratkaisimesta, hyökkäisimme tähän ongelmaan luomalla laskentataulukon, joka seuraa tuotevalikoimaan liittyvää tuottoa ja resurssien käyttöä. Sitten käyttäisimme kokeilua ja virhettä tuotevalikoiman vaihtelemiseksi voiton optimoimiseksi käyttämättä enemmän työvoimaa tai raaka-ainetta kuin on saatavilla ja tuottamatta mitään lääkettä, joka ylittää kysynnän. Ratkaisinta käytetään tässä prosessissa vain kokeilu- ja virhevaiheessa. Ratkaisin on optimointimoduuli, joka suorittaa virheettömän kokeilu- ja virhehaun.
Avain tuotevalikoimaongelman ratkaisemiseen on laskea tehokkaasti mihin tahansa tuotevalikoimaan liittyvä resurssien käyttö ja tuotto. Tärkeä työkalu, jonka avulla voimme tehdä tämän laskennan, on TULOJEN.SUMMA-funktio. TULOJEN.SUMMA-funktio kertoo solualueiden vastaavat arvot ja palauttaa näiden arvojen summan. Kullakin TULOJEN.SUMMA arvioinnissa käytetyllä solualueella on oltava samat mitat, mikä tarkoittaa, että voit käyttää TULOJEN.SUMMA kahden rivin tai kahden sarakkeen kanssa, mutta et yhden sarakkeen ja yhden rivin kanssa.
Esimerkki siitä, miten voimme käyttää TULOJEN.SUMMA-funktiota tuotevalikoimassamme, yritetään laskea resurssien käyttö. Työkäyttömme lasketaan
(Käytetty työvoima per punta lääkettä 1)*(Lääke 1 punta tuotettu)+ (Käytetty työvoima per punta huumeiden 2)*(Lääke 2 kiloa tuotettu) + ... (Käytetty työvoima per punta lääkettä 6)*(Lääke 6 kiloa tuotettu)
Työvoiman käyttö voitaisiin laskea tylsämmin muodossa D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4*I4. Vastaavasti raaka-aineiden käyttö voidaan laskea muodossa D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Näiden kaavojen kirjoittaminen kuuden tuotteen laskentataulukkoon vie kuitenkin aikaa. Kuvittele, kuinka kauan kestäisi, jos työskentelisit yrityksessä, joka on tuottanut esimerkiksi 50 tuotetta tehtaallaan. Paljon helpompi tapa laskea työvoiman ja raaka-aineiden käyttö on kopioida kaava D14:stä D15:een TULOJEN.SUMMA($D$2:$I$2,D4:I4). Tämä kaava laskee D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4*I4 (joka on työkäytömme), mutta se on paljon helpompi syöttää! Huomaa, että käytän $-merkkiä alueella D2:I2 niin, että kun kopioin kaavan, tallennan edelleen tuotesekoituksen riviltä 2. Solun D15 kaava laskee raaka-aineiden käytön.
Samalla tavalla voittomme määräytyvät
(Huumeiden 1 voitto per punta)*(Lääke 1 punta tuotettu) + (Drug 2 voitto per pauna)*(Lääke 2 kiloa tuotettu) + ... (Huumeiden 6 voitto per pauna)*(Lääke 6 kiloa tuotettu)
Tuotto lasketaan helposti solussa D12 kaavalla TULOJEN.SUMMA(D9:I9,$D$2:$I$2).
Voimme nyt tunnistaa tuotevalikoimamme Ratkaisin-mallin kolme osaa.
-
Kohdesolu. Tavoitteemme on maksimoida voitto (laskettuna solussa D12).
-
Solujen muuttaminen. Kunkin tuotteen tuottama kilomäärä (lueteltu solualueella D2:I2)
-
Rajoitukset. Meillä on seuraavat rajoitukset:
-
Älä käytä enempää työvoimaa tai raaka-ainetta kuin on saatavilla. Eli solujen D14:D15 arvojen (käytettyjen resurssien) on oltava pienempiä tai yhtä suuria kuin solujen F14:F15 (käytettävissä olevat resurssit) arvot.
-
Älä tuota enemmän lääkettä kuin on kysyntää. Eli solujen D2:I2 arvojen (kunkin lääkkeen tuottaman kilon) on oltava pienempi tai yhtä suuri kuin kunkin lääkkeen kysyntä (lueteltu soluissa D8:I8).
-
Emme voi tuottaa negatiivista määrää mitään lääkettä.
-
Näytän, miten voit lisätä kohdesolun, muuttaa soluja ja rajoituksia Ratkaisimeen. Sitten sinun tarvitsee vain napsauttaa Ratkaise-painiketta löytääksesi voittoa maksimoivan tuotevalikoiman!
Aloita valitsemalla Tiedot-välilehti ja valitsemalla Analyysi-ryhmässä Ratkaisin.
Huomautus: Kuten luvussa 26 "Johdanto optimointiin Excelin ratkaisimen kanssa" kerrotaan, Ratkaisin asennetaan napsauttamalla Microsoft Office -painiketta, sitten Excelin asetuksia ja sen jälkeen apuohjelmia. Valitse Hallinta-luettelosta Excel-apuohjelmat, valitse Ratkaisin-apuohjelma-ruutu ja valitse sitten OK.
Ratkaisimen parametrit -valintaikkuna tulee näkyviin kuvan 27–2 mukaisesti.
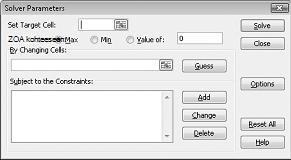
Napsauta Määritä kohdesolu -ruutua ja valitse sitten tuottosolu (solu D12). Napsauta Muokkaa soluja -ruutua ja osoita sitten aluetta D2:I2, joka sisältää kunkin lääkkeen tuottamat kilot. Valintaikkunan pitäisi nyt näyttää kuvalta 27–3.
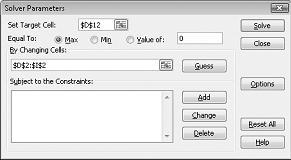
Olemme nyt valmiita lisäämään rajoitteita malliin. Napsauta Lisää-painiketta. Näet Lisää rajoite -valintaikkunan kuvassa 27-4.
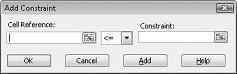
Lisää resurssien käyttörajoitukset napsauttamalla Soluviittaus-ruutua ja valitsemalla sitten alue D14:D15. Valitse keskimmäisessä luettelossa <= . Napsauta Rajoite-ruutua ja valitse sitten solualue F14:F15. Lisää rajoitus -valintaikkunan pitäisi nyt näyttää kuvalta 27–5.
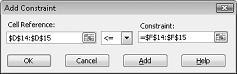
Olemme nyt varmistaneet, että kun Ratkaisin kokeilee eri arvoja muuttuville soluille, otetaan huomioon vain yhdistelmät, jotka täyttävät sekä D14-<=F14 (käytetty työvoima on pienempi tai yhtä suuri kuin käytettävissä oleva työvoima) että D15<=F15 (käytetty raaka-aine on pienempi tai yhtä suuri kuin käytettävissä oleva raaka-aine). Valitse Lisää, jos haluat lisätä kysyntärajoitukset. Täytä Lisää rajoite -valintaikkuna kuvassa 27–6 esitetyllä tavalla.
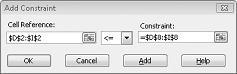
Näiden rajoitusten lisääminen varmistaa, että kun Ratkaisin kokeilee eri yhdistelmiä muuttuville soluarvoille, huomioon otetaan vain seuraavat parametrit täyttävät yhdistelmät:
-
D2<=D8 (lääkkeen 1 tuottama määrä on pienempi tai yhtä suuri kuin lääkkeen 1 kysyntä)
-
E2<=E8 (lääke 2: n tuotemäärä on pienempi tai yhtä suuri kuin huumeiden 2 kysyntä)
-
F2<=F8 (valmistettu lääke 3 on pienempi tai yhtä suuri kuin huumeiden 3 kysyntä)
-
G2<=G8 (valmistettu lääke 4 on pienempi tai yhtä suuri kuin huumeiden 4 kysyntä)
-
H2<=H8 (valmistettu lääke 5 on pienempi tai yhtä suuri kuin huumeiden 5 kysyntä)
-
I2<=I8 (valmistettu lääke 6 on pienempi tai yhtä suuri kuin huumeiden 6 kysyntä)
Valitse Lisää rajoitus -valintaikkunassa OK. Ratkaisin-ikkunan pitäisi näyttää kuvalta 27–7.
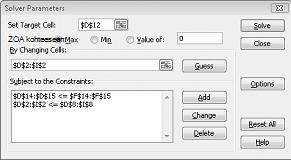
Määritämme Ratkaisimen asetukset -valintaikkunaan rajoituksen, jonka mukaan solujen muuttamisen on oltava ei-negatiivista. Napsauta Ratkaisimen parametrit -valintaikkunan Asetukset-painiketta. Valitse Oleta lineaarinen malli -ruutu ja Oleta ei-negatiivinen -ruutu seuraavan sivun kuvassa 27-8 esitetyllä tavalla. Valitse OK.
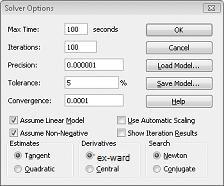
Jos valitset Oleta ei-negatiivinen -ruudun, Ratkaisin ottaa huomioon vain muuttuvien solujen yhdistelmät, joissa kussakin muuttuvassa solussa oletetaan olevan muu kuin negatiivinen arvo. Tarkistimme Oleta lineaarinen malli -ruudun, koska tuotesekoitusongelma on erityinen Ratkaisin-ongelma, jota kutsutaan lineaarinen malliksi. Ratkaisinmalli on lineaarinen seuraavissa olosuhteissa:
-
Kohdesolu lasketaan laskemalla yhteen lomakkeen termit (solun muuttaminen)*(vakio).
-
Jokainen rajoitus täyttää lineaarisen mallin vaatimuksen. Tämä tarkoittaa sitä, että kukin rajoitus arvioidaan lisäämällä yhteen lomakkeen ehdot (solun muuttaminen)*(vakio) ja vertaamalla summia vakioon.
Miksi tämä Ratkaisin-ongelma on lineaarinen? Kohdesolumme (tuotto) lasketaan muodossa
(Huumeiden 1 voitto per punta)*(Lääke 1 punta tuotettu) + (Drug 2 voitto per pauna)*(Lääke 2 kiloa tuotettu) + ... (Huumeiden 6 voitto per pauna)*(Lääke 6 kiloa tuotettu)
Tämä laskenta noudattaa kaavaa, jossa kohdesolun arvo johdetaan lisäämällä yhteen lomakkeen termit (solun muuttaminen)*(vakio).
Työrajoite arvioidaan vertaamalla arvoa johdettu (Käytetty kilo huumeiden 1)*(Lääke 1 punta tuotettu) + (Työvoima käytetty per punta huumeiden 2)*(Lääke 2 kiloa tuotettu)+ ... (Työväenpuolue meitäed per pauna huumeiden 6)*(Lääke 6 kiloa tuotettu) työvoimaan saatavilla.
Siksi työrajoitus arvioidaan lisäämällä yhteen lomakkeen ehdot (solun muuttaminen)*(vakio) ja vertaamalla summia vakioon. Sekä työrajoitus että raaka-ainerajoitus täyttävät lineaarisen mallin vaatimuksen.
Kysyntärajoitukset ovat muodossa
(Lääke 1 tuotettu)<=(Lääke 1 Kysyntä) (Lääke 2 tuotettu)<=(Drug 2 Demand) §(Lääke 6 tuotettu)<=(Drug 6 Demand)
Jokainen kysyntärajoitus täyttää myös lineaarisen mallin vaatimuksen, koska jokainen niistä arvioidaan lisäämällä yhteen lomakkeen ehdot (solun muuttaminen)*(vakio) ja vertaamalla summia vakioon.
Kun olemme osoittaneet, että tuotevalikoimamallimme on lineaarinen malli, miksi meidän pitäisi välittää?
-
Jos Ratkaisin-malli on lineaarinen ja valitsemme Ota lineaarinen malli -vaihtoehdon, Ratkaisin löytää varmasti optimaalisen ratkaisun Ratkaisin-malliin. Jos Ratkaisin-malli ei ole lineaarinen, Ratkaisin saattaa löytää optimaalisen ratkaisun.
-
Jos Ratkaisin-malli on lineaarinen ja valitsemme Ota lineaarinen malli -vaihtoehdon, Ratkaisin käyttää erittäin tehokasta algoritmia (simplex-menetelmää) mallin optimaalisen ratkaisun löytämiseksi. Jos Ratkaisin-malli on lineaarinen eikä valitse Ota lineaarinen malli -valintaa, Ratkaisin käyttää erittäin tehotonta algoritmia (GRG2-menetelmää) ja voi olla vaikea löytää mallin optimaalista ratkaisua.
Kun ratkaisimen asetukset -valintaikkunassa on valittu OK, palaamme Ratkaisin-päävalintaikkunaan, joka näkyy aiemmin kuvassa 27–7. Kun valitsemme Ratkaise, Ratkaisin laskee optimaalisen ratkaisun (jos sellainen on olemassa) tuotevalikoimamallillemme. Kuten totesin luvussa 26, optimaalinen ratkaisu tuotevalikoimamalliin olisi joukko muuttuvia soluarvoja (kustakin lääkkeestä tuotetut kilot), jotka maksimoivat voiton kaikista toteuttamiskelpoisista ratkaisuista. Jälleen mahdollinen ratkaisu on joukko muuttuvia soluarvoja, jotka täyttävät kaikki rajoitukset. Kuvassa 27–9 esitetyt muuttuvat soluarvot ovat toteuttamiskelpoinen ratkaisu, koska kaikki tuotantotasot eivät ole negatiivisia, tuotantotasot eivät ylitä kysyntää ja resurssien käyttö ei ylitä käytettävissä olevia resursseja.
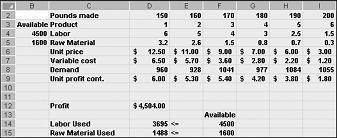
Seuraavalla sivulla kuvassa 27–10 näkyvät muuttuvat soluarvot edustavat mahdotonta ratkaisua seuraavista syistä:
-
Tuotamme enemmän Lääke 5: stä kuin sen kysyntä.
-
Käytämme enemmän työvoimaa kuin mitä on saatavilla.
-
Käytämme enemmän raaka-ainetta kuin mitä on saatavilla.
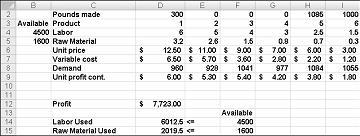
Kun olet valinnut Ratkaise, Ratkaisin löytää nopeasti optimaalisen ratkaisun kuvassa 27-11. Valitse Säilytä ratkaisinratkaisu, jotta voit säilyttää optimaaliset ratkaisuarvot laskentataulukossa.
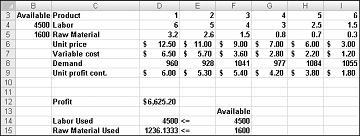
Lääkeyhtiömme voi maksimoida kuukausittaisen voittonsa tasolla 6 625,20 dollaria tuottamalla 596,67 kiloa lääkettä 4, 1084 kiloa lääkettä 5, eikä mitään muita lääkkeitä! Emme pysty määrittämään, voimmeko saavuttaa 6 625,20 dollarin enimmäisvoiton muilla tavoin. Voimme vain olla varmoja siitä, että rajallisilla resursseillamme ja kysynnällämme ei ole mitään keinoa ansaita enempää kuin 6 627,20 dollaria tässä kuussa.
Oletetaan, että kunkin tuotteen kysyntä on täytettävä. (Katso ei mahdollista ratkaisua - laskentataulukko tiedoston Prodmix.xlsx.) Sen jälkeen meidän on muutettava kysyntärajoitukset kohdasta D2:I2<=D8:I8 arvoon D2:I2>=D8:I8. Voit tehdä tämän avaamalla Ratkaisimen, valitsemalla D2:I2-<=D8:I8-rajoituksen ja valitsemalla sitten Muuta. Kuvassa 27–12 näkyvä Muuta rajoitetta -valintaikkuna tulee näkyviin.
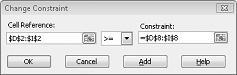
Valitse >=ja valitse sitten OK. Olemme nyt varmistaneet, että Ratkaisin harkitsee vain kaikkia vaatimuksia täyttävien solujen arvojen muuttamista. Kun valitset Ratkaise, näet viestin "Ratkaisin ei löytänyt toteuttamiskelpoista ratkaisua". Tämä viesti ei tarkoita, että olisimme tehneet virheen mallissamme, vaan että rajallisten resurssien avulla emme pysty vastaamaan kaikkien tuotteiden kysyntään. Ratkaisin kertoo meille yksinkertaisesti, että jos haluamme vastata kunkin tuotteen kysyntään, meidän on lisättävä työvoimaa, enemmän raaka-aineita tai enemmän molempia.
Katsotaan, mitä tapahtuu, jos sallimme rajoittamattoman kysynnän kullekin tuotteelle ja sallimme negatiivisten määrien tuottamisen jokaisesta lääkkeestä. (Tämä Ratkaisin-ongelma näkyy Määritä arvot, älä yhdistä -laskentataulukossa tiedostossa Prodmix.xlsx.) Jos haluat löytää optimaalisen ratkaisun tähän tilanteeseen, avaa Ratkaisin, napsauta Asetukset-painiketta ja tyhjennä Oleta ei-negatiivinen -ruudun valinta. Valitse Ratkaisimen parametrit -valintaikkunassa kysyntärajoitus D2:I2<=D8:I8 ja poista sitten rajoitus valitsemalla Poista. Kun valitset Ratkaise, Ratkaisin palauttaa viestin "Määritä solun arvot, älä lähennä". Tämä sanoma tarkoittaa, että jos kohdesolu halutaan suurentaa (kuten esimerkissämme), on olemassa toteuttamiskelpoisia ratkaisuja, joissa on satunnaisesti suuria kohdesoluarvoja. (Jos kohdesolu halutaan pienentää, sanoma "Määritä solun arvot, älä yhdistä" tarkoittaa, että on olemassa mahdollisia ratkaisuja, joissa on satunnaisesti pieniä kohdesoluarvoja.) Kun sallimme huumeiden negatiivisen tuotannon, me itse asiassa "luomme" resursseja, joita voidaan käyttää satunnaisesti suurten muiden huumeiden tuottamiseen. Rajoittamattoman vaatimuksemme vuoksi voimme tehdä rajoittamattoman voiton. Todellisessa tilanteessa emme voi tienata ääretöntä rahasummaa. Jos näet "Määritä arvot, älä yhdistä", mallissasi on virhe.
-
Oletetaan, että lääkeyhtiömme voi ostaa jopa 500 tuntia työvoimaa hintaan 1 dollaria enemmän tunnissa kuin nykyiset työvoimakustannukset. Miten voimme maksimoida voiton?
-
Sirutehtaassa neljä teknikkoa (A, B, C ja D) tuottaa kolme tuotetta (tuotteet 1, 2 ja 3). Tässä kuussa siruvalmistaja voi myydä 80 yksikköä tuotetta 1, 50 yksikköä tuotetta 2 ja enintään 50 yksikköä tuotetta 3. Teknikko A voi tehdä vain tuotteita 1 ja 3. Teknikko B voi tehdä vain tuotteita 1 ja 2. Teknikko C voi tehdä vain tuotteen 3. Teknikko D voi tehdä vain tuotteen 2. Kunkin tuoteyksikön osalta tuotteilla on seuraava voitto: Tuote 1, 6 dollaria; Tuote 2, $7; ja tuote 3, 10 dollaria. Kunkin teknikon tuotteen valmistukseen tarvittava aika (tunteina) on seuraava:
Tuote
Teknikko A
Teknikko B
Teknikko C
Teknikko D
1
2
2,5
Ei voi tehdä
Ei voi tehdä
2
Ei voi tehdä
3
Ei voi tehdä
3,5
3
3
Ei voi tehdä
4
Ei voi tehdä
-
Jokainen teknikko voi työskennellä jopa 120 tuntia kuukaudessa. Miten siruvalmistaja voi maksimoida kuukausittaisen voittonsa? Oletetaan, että voidaan tuottaa murtolukumäärä yksiköitä.
-
Tietokonevalmistuslaitos tuottaa hiiriä, näppäimistöjä ja videopelien ohjainsauvoja. Yksikkökohtainen voitto, yksikkökohtainen työkäyttö, kuukausittainen kysyntä ja konekohtainen käyttö esitetään seuraavassa taulukossa:
Hiiret
Näppäimistöt
Peliohjaimet
Voitto/yksikkö
8 dollaria
11 dollaria
9 dollaria
Työvoiman käyttö/yksikkö
.2 tuntia
.3 tuntia
.24 tunnin kuluttua
Koneen aika/yksikkö
.04 tuntia
.055 tuntia
.04 tuntia
Kuukausittainen kysyntä
15 000
27,000
11,000
-
Joka kuukausi käytettävissä on yhteensä 13 000 työtuntia ja 3 000 tuntia koneaikaa. Miten valmistaja voi maksimoida kuukausittaisen voittonsa tehtaalta?
-
Ratkaise lääkeesimerkkimme olettaen, että kullekin lääkkeelle on vastattava 200 yksikön vähimmäiskysyntään.
-
Jason tekee timanttirannekkeita, kaulakoruja ja korvakoruja. Hän haluaa työskennellä enintään 160 tuntia kuukaudessa. Hänellä on 800 unssia timantteja. Kunkin tuotteen tuottamiseen tarvittavat voitot, työaika ja unssit timantteja annetaan alla. Jos kunkin tuotteen kysyntä on rajaton, miten Jason voi maksimoida voittonsa?
Tuote
Yksikkötuotto
Työtunnit yksikköä kohti
Unssit timantteja yksikköä kohti
Rannerengas
300 €
.35
1,2
Kaulakoru
200 €
.15
.75
Korvakorut
100 €
.05
.5










