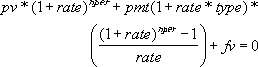Fonction VA

Syntaxe

PV(rate,nper,pmt,fv,type)

taux     est le taux d’intérêt par période. Par exemple, si vous obtenez un emprunt pour l’achat d’une voiture à un taux d’intérêt annuel de 10 % et que vos remboursements sont mensuels, le taux d’intérêt mensuel sera de 10 %/12, soit 0,83 %. Le chiffre entré dans la formule en tant que taux peut être 10 %/12, 0,83 % ou 0,0083.

npm     est le nombre total de périodes de paiement dans une annuité. Si, pour l’achat d’une voiture, vous obtenez un emprunt sur quatre ans, remboursable mensuellement, cet emprunt s’étend sur 4*12 (ou 48) périodes. Le chiffre entré dans la formule en tant qu’argument npm sera 48.

Pmt     est le paiement effectué à chaque période et ne peut pas changer pendant la durée de l’annuité. En règle générale, vpm comprend le montant principal et les intérêts mais exclut toute autre charge ou tout autre impôt. Par exemple, les paiements mensuels sur un prêt auto de 10 000 $ et de quatre ans à 12 % sont de 263,33 $. Vous devez entrer -263,33 dans la formule en tant que pmt. Si l’argument vpm est omis, vous devez inclure l’argument vc.

vc     est la valeur future, ou un solde en espèces que vous souhaitez atteindre après le dernier paiement. Si vc est omis, la valeur par défaut est 0 (par exemple, la valeur capitalisée d’un emprunt est égale à 0). Ainsi, si vous souhaitez économiser 50 000 € pour financer un projet précis dans 18 ans, 50 000 € est la valeur capitalisée à atteindre. Vous pouvez faire une estimation du taux d’intérêt et déterminer le montant que vous devez épargner chaque mois. Si l’argument vc est omis, vous devez inclure l’argument vpm.

Type  est le nombre 0 ou 1 et indique quand les paiements sont dus.

Remarques

• Veillez à utiliser la même unité pour les arguments taux et npm. Si vous effectuez des remboursements mensuels pour un emprunt sur quatre ans à un taux d’intérêt annuel de 12 %, utilisez 12 %/12 pour l’argument taux et 4*12 pour l’argument npm. Si vous effectuez des remboursements annuels pour le même emprunt, utilisez 12 % pour l’argument taux et 4 pour l’argument npm.

• Les fonctions suivantes s’appliquent aux annuités : FV ; INTPER ; VPM ; PRINCPER ; PV; et TAUX. Une annuité est un paiement constant pendant une période ininterrompue. Par exemple, le remboursement d’un emprunt pour l’achat d’une voiture ou d’un emprunt immobilier est constitué d’annuités. Pour plus d’informations, reportez-vous à la description de chaque fonction d’annuité.

• Dans les fonctions d’annuité, l’argent que vous versez, comme un dépôt d’épargne, est représenté par un nombre négatif ; l’argent que vous recevez, tel qu’un dividende case activée, est représenté par un nombre positif. Par exemple, un dépôt de 1 000 $ à la banque serait représenté par l’argument -1000 si vous êtes le déposant et par l’argument 1000 si vous êtes la banque.

• Un argument financier est résolu par rapport aux autres. Si l’argument taux est différent de 0 :

  

  Si l’argument taux est égal à 0 :

  (vpm * npm) + va + vc = 0

Exemple

Dans l’exemple suivant :

• Pmt est l’argent versé à partir d’une rente d’assurance à la fin de chaque mois.

• Taux est le taux d’intérêt gagné sur l’argent versé.

• Nper est les années où l’argent sera versé.

Le taux d’intérêt est divisé par 12 pour obtenir un taux mensuel. Les années où l’argent est versé sont multipliées par 12 pour obtenir le nombre de paiements.

Le résultat est négatif, car il représente de l’argent que vous paieriez, un flux de trésorerie sortant. Si vous êtes invité à payer (60 000) pour l’annuité, vous estimez que ce ne serait pas un bon investissement, car la valeur actuelle de l’annuité (59 777,15) est inférieure à ce que vous êtes invité à payer.