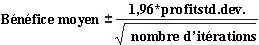Cet article a été adapté de Microsoft Excel Data Analysis and Business Modeling par Wayne L. Winston.
-
Qui utilise la simulation Monte Carlo ?
-
Que se passe-t-il lorsque vous tapez =RAND() dans une cellule ?
-
Comment pouvez-vous simuler des valeurs d’une variable aléatoire discrète ?
-
Comment pouvez-vous simuler des valeurs d’une variable aléatoire normale ?
-
Comment un message d’accueil carte entreprise peut-il déterminer le nombre de cartes à produire ?
Nous aimerions estimer avec précision les probabilités d’événements incertains. Par exemple, quelle est la probabilité que les flux de trésorerie d’un nouveau produit aient une valeur actuelle nette (VAN) positive ? Quel est le facteur de risque de notre portefeuille d’investissement ? La simulation monte-carlo nous permet de modéliser des situations qui présentent une incertitude, puis de les jouer sur un ordinateur des milliers de fois.
Remarque : Le nom De Monte Carlo simulation vient des simulations informatiques effectuées au cours des années 1930 et 1940 pour estimer la probabilité que la réaction en chaîne nécessaire à l’explosion d’une bombe atomique fonctionne avec succès. Les physiciens impliqués dans ce travail étaient de grands fans de jeux d’argent, alors ils ont donné aux simulations le nom de code Monte Carlo.
Dans les cinq prochains chapitres, vous verrez des exemples d’utilisation d’Excel pour effectuer des simulations Monte Carlo.
De nombreuses entreprises utilisent la simulation Monte Carlo comme une partie importante de leur processus de prise de décision. Voici quelques exemples.
-
General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb et Eli Lilly utilisent la simulation pour estimer le rendement moyen et le facteur de risque des nouveaux produits. Chez GM, cette information est utilisée par le pdg pour déterminer quels produits sont mis sur le marché.
-
GM utilise la simulation pour des activités telles que la prévision du bénéfice net pour la société, la prédiction des coûts structurels et d’achat, et la détermination de sa sensibilité à différents types de risques (comme les variations des taux d’intérêt et les fluctuations des taux de change).
-
Lilly utilise la simulation pour déterminer la capacité optimale de chaque médicament.
-
Proctor and Gamble utilise la simulation pour modéliser et couvrir de manière optimale le risque de change.
-
Sears utilise la simulation pour déterminer le nombre d’unités de chaque gamme de produits à commander auprès des fournisseurs, par exemple, le nombre de paires de pantalons Dockers qui doivent être commandés cette année.
-
Les compagnies pétrolières et pharmaceutiques utilisent la simulation pour valoriser les « options réelles », telles que la valeur d’une option d’expansion, de contrat ou de report d’un projet.
-
Les planificateurs financiers utilisent la simulation Monte Carlo pour déterminer les stratégies de placement optimales pour la retraite de leurs clients.
Lorsque vous tapez la formule =RAND() dans une cellule, vous obtenez un nombre qui est également susceptible de supposer n’importe quelle valeur comprise entre 0 et 1. Ainsi, environ 25 pour cent du temps, vous devriez obtenir un nombre inférieur ou égal à 0,25 ; environ 10 % du temps, vous devriez obtenir un nombre d’au moins 0,90, et ainsi de suite. Pour illustrer le fonctionnement de la fonction RAND, examinez le fichier Randdemo.xlsx, illustré dans la figure 60-1.
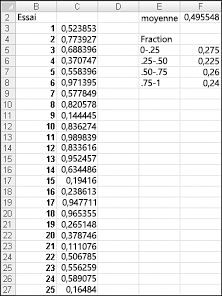
Remarque : Lorsque vous ouvrez le fichier Randdemo.xlsx, vous ne voyez pas les mêmes nombres aléatoires indiqués dans la figure 60-1. La fonction RAND recalcule toujours automatiquement les nombres qu’elle génère lorsqu’une feuille de calcul est ouverte ou lorsque de nouvelles informations sont entrées dans la feuille de calcul.
Tout d’abord, copiez de la cellule C3 vers C4 :C402 la formule =RAND(). Ensuite, vous nommez la plage C3 :C402 Data. Ensuite, dans la colonne F, vous pouvez suivre la moyenne des 400 nombres aléatoires (cellule F2) et utiliser la fonction NB.SI pour déterminer les fractions comprises entre 0 et 0,25, 0,25 et 0,50, 0,50 et 0,75 et 0,75 et 0,75 et 1. Lorsque vous appuyez sur la touche F9, les nombres aléatoires sont recalculés. Notez que la moyenne des 400 nombres est toujours d’environ 0,5, et qu’environ 25 pour cent des résultats sont par intervalles de 0,25. Ces résultats sont cohérents avec la définition d’un nombre aléatoire. Notez également que les valeurs générées par RAND dans différentes cellules sont indépendantes. Par exemple, si le nombre aléatoire généré dans la cellule C3 est un grand nombre (par exemple, 0,99), il ne nous indique rien sur les valeurs des autres nombres aléatoires générés.
Supposons que la demande pour un calendrier soit régie par la variable aléatoire discrète suivante :
|
Demande |
probabilité |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0,35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Comment pouvons-nous faire en sorte qu’Excel joue ou simule cette demande de calendriers plusieurs fois ? L’astuce consiste à associer chaque valeur possible de la fonction RAND à une demande possible de calendriers. L’affectation suivante garantit qu’une demande de 10 000 se produira 10 % du temps, et ainsi de suite.
|
Demande |
Nombre aléatoire attribué |
|---|---|
|
10 000 |
Inférieur à 0,10 |
|
20 000 |
Supérieur ou égal à 0,10 et inférieur à 0,45 |
|
40,000 |
Supérieur ou égal à 0,45 et inférieur à 0,75 |
|
60 000 |
Supérieur ou égal à 0,75 |
Pour illustrer la simulation de la demande, examinez le fichier Discretesim.xlsx, illustré à la figure 60-2 de la page suivante.
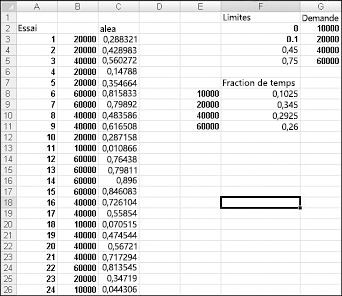
La clé de notre simulation consiste à utiliser un nombre aléatoire pour lancer une recherche à partir de la plage de table F2 :G5 (nommée recherche). Les nombres aléatoires supérieurs ou égaux à 0 et inférieurs à 0,10 produisent une demande de 10 000 ; les nombres aléatoires supérieurs ou égaux à 0,10 et inférieurs à 0,45 produisent une demande de 20 000 ; les nombres aléatoires supérieurs ou égaux à 0,45 et inférieurs à 0,75 produisent une demande de 40 000 ; et les nombres aléatoires supérieurs ou égaux à 0,75 produisent une demande de 60 000. Vous générez 400 nombres aléatoires en copiant de C3 vers C4 :C402 la formule RAND(). Vous générez ensuite 400 essais, ou itérations, de la demande de calendrier en copiant de B3 vers B4 :B402 la formule RECHERCHEV(C3,lookup,2). Cette formule garantit que tout nombre aléatoire inférieur à 0,10 génère une demande de 10 000, tout nombre aléatoire compris entre 0,10 et 0,45 génère une demande de 20 000, et ainsi de suite. Dans la plage de cellules F8 :F11, utilisez la fonction NB.SI pour déterminer la fraction de nos 400 itérations produisant chaque demande. Lorsque nous appuyons sur F9 pour recalculer les nombres aléatoires, les probabilités simulées sont proches de nos probabilités de demande supposées.
Si vous tapez dans une cellule la formule LOI.NORMALE.INVERSE(rand(),mu,sigma), vous générez une valeur simulée d’une variable aléatoire normale ayant une valeur moyenne mu et un sigma d’écart type. Cette procédure est illustrée dans le fichier Normalsim.xlsx, illustré dans la figure 60-3.
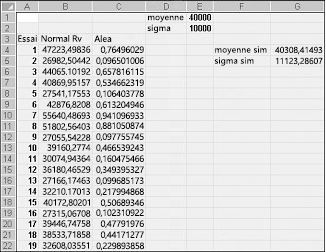
Supposons que nous souhaitions simuler 400 essais, ou itérations, pour une variable aléatoire normale avec une moyenne de 40 000 et un écart type de 10 000. (Vous pouvez taper ces valeurs dans les cellules E1 et E2, et nommer ces cellules respectivement mean et sigma.) La copie de la formule =RAND() de C4 vers C5 :C403 génère 400 nombres aléatoires différents. La copie de B4 vers B5 :B403 la formule LOI.NORMALE.INVERSE(C4,moyenne,sigma) génère 400 valeurs d’essai différentes à partir d’une variable aléatoire normale avec une moyenne de 40 000 et un écart type de 10 000. Lorsque nous appuyons sur la touche F9 pour recalculer les nombres aléatoires, la moyenne reste proche de 40 000 et l’écart type proche de 10 000.
Essentiellement, pour un nombre aléatoire x, la formule LOI.NORMALE.INVERSE(p,mu,sigma) génère le pième centile d’une variable aléatoire normale avec un mu moyen et un sigma d’écart type. Par exemple, le nombre aléatoire 0,77 dans la cellule C4 (voir la figure 60-3) génère dans la cellule B4 environ le 77e centile d’une variable aléatoire normale avec une moyenne de 40 000 et un écart type de 10 000.
Dans cette section, vous allez voir comment la simulation Monte Carlo peut être utilisée comme outil de prise de décision. Supposons que la demande d’un carte pour la Saint-Valentin soit régie par la variable aléatoire discrète suivante :
|
Demande |
probabilité |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0,35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Le carte de salutation se vend au prix de 4,00 $, et le coût variable de production de chaque carte est de 1,50 $. Les cartes restantes doivent être éliminées au coût de 0,20 $ par carte. Combien de cartes doivent être imprimées ?
Fondamentalement, nous simulons chaque quantité de production possible (10 000, 20 000, 40 000 ou 60 000) plusieurs fois (par exemple, 1 000 itérations). Ensuite, nous déterminons la quantité de commandes qui génère le bénéfice moyen maximal sur les 1 000 itérations. Vous trouverez les données de cette section dans le fichier Valentine.xlsx, illustré dans la figure 60-4. Vous affectez les noms de plage dans les cellules B1 :B11 aux cellules C1 :C11. La recherche de nom est affectée à la plage de cellules G3 :H6. Nos paramètres de prix de vente et de coût sont entrés dans les cellules C4 :C6.
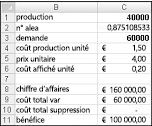
Vous pouvez entrer une quantité de production d’essai (40 000 dans cet exemple) dans la cellule C1. Ensuite, créez un nombre aléatoire dans la cellule C2 avec la formule =RAND(). Comme décrit précédemment, vous simulez la demande pour le carte dans la cellule C3 avec la formule RECHERCHEV(rand,lookup,2). (Dans la formule RECHERCHEV, rand est le nom de cellule affecté à la cellule C3, et non la fonction RAND.)
Le nombre d’unités vendues est le plus petit de notre production et de notre demande. Dans la cellule C8, vous calculez notre chiffre d’affaires avec la formule MIN(production,demande)*unit_price. Dans la cellule C9, vous calculez le coût de production total avec la formule produite*unit_prod_cost.
Si nous produisons plus de cartes que la demande, le nombre d’unités restantes est égal à la production moins la demande ; dans le cas contraire, aucune unité n’est laissée. Nous calculons notre coût d’élimination dans la cellule C10 avec la formule unit_disp_cost*SI(produit>demande,production-demande,0). Enfin, dans la cellule C11, nous calculons notre bénéfice sous forme de chiffre d’affaires total_var_cost total_disposing_cost.
Nous aimerions un moyen efficace d’appuyer sur F9 plusieurs fois (par exemple, 1 000) pour chaque quantité de production et de décompter le bénéfice attendu pour chaque quantité. Il s’agit d’une situation dans laquelle une table de données bidirectionnel vient à notre secours. (Pour plus d’informations sur les tables de données, consultez le chapitre 15, « Analyse de la sensibilité avec des tables de données ». La table de données utilisée dans cet exemple est illustrée dans la figure 60-5.
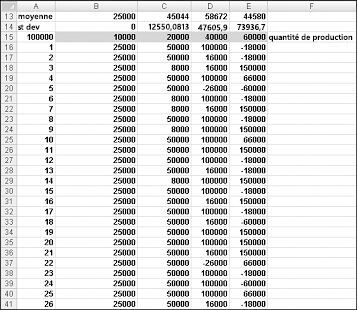
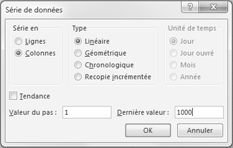
Dans la plage de cellules A16 :A1015, entrez les nombres 1 à 1000 (correspondant à nos 1 000 essais). Un moyen simple de créer ces valeurs consiste à commencer par entrer 1 dans la cellule A16. Sélectionnez la cellule, puis sous l’onglet Accueil du groupe Édition , cliquez sur Remplissage, puis sélectionnez Série pour afficher la boîte de dialogue Série . Dans la boîte de dialogue Série , illustrée dans la figure 60-6, entrez une valeur d’étape de 1 et une valeur d’arrêt de 1 000. Dans la zone Série dans , sélectionnez l’option Colonnes , puis cliquez sur OK. Les nombres 1 à 1000 seront entrés dans la colonne A à partir de la cellule A16.
Ensuite, nous allons entrer nos quantités de production possibles (10 000, 20 000, 40 000, 60 000) dans les cellules B15 :E15. Nous voulons calculer les bénéfices pour chaque numéro d’essai (1 à 1000) et chaque quantité de production. Nous faisons référence à la formule de profit (calculée dans la cellule C11) dans la cellule supérieure gauche de notre table de données (A15) en entrant =C11.
Nous sommes maintenant prêts à tromper Excel pour simuler 1 000 itérations de demande pour chaque quantité de production. Sélectionnez la plage de tables (A15 :E1014), puis dans le groupe Outils de données sous l’onglet Données, cliquez sur Analyse What If, puis sélectionnez Table de données. Pour configurer une table de données bidirectionnel, choisissez notre quantité de production (cellule C1) comme cellule d’entrée de ligne et sélectionnez n’importe quelle cellule vide (nous avons choisi la cellule I14) comme cellule d’entrée de colonne. Après avoir cliqué sur OK, Excel simule 1 000 valeurs de demande pour chaque quantité de commande.
Pour comprendre pourquoi cela fonctionne, considérez les valeurs placées par la table de données dans la plage de cellules C16 :C1015. Pour chacune de ces cellules, Excel utilise une valeur de 20 000 dans la cellule C1. En C16, la valeur de cellule d’entrée de colonne 1 est placée dans une cellule vide et le nombre aléatoire de la cellule C2 recalcule. Le bénéfice correspondant est ensuite enregistré dans la cellule C16. Ensuite, la valeur d’entrée de cellule de colonne 2 est placée dans une cellule vide, et le nombre aléatoire en C2 recalcule. Le bénéfice correspondant est entré dans la cellule C17.
En copiant de la cellule B13 vers C13 :E13 la formule AVERAGE(B16 :B1015), nous calculons le bénéfice simulé moyen pour chaque quantité de production. En copiant de la cellule B14 vers C14 :E14 la formule ECARTYPE(B16 :B1015), nous calculons l’écart type de nos bénéfices simulés pour chaque quantité de commande. Chaque fois que nous appuyons sur F9, 1 000 itérations de demande sont simulées pour chaque quantité de commande. Produire 40 000 cartes génère toujours le bénéfice attendu le plus important. Par conséquent, il semble que la production de 40 000 cartes soit la bonne décision.
L’impact du risque sur notre décision Si nous avons produit 20 000 cartes au lieu de 40 000 cartes, notre bénéfice attendu baisse d’environ 22 %, mais notre risque (mesuré par l’écart type du profit) chute de près de 73 %. Par conséquent, si nous sommes extrêmement opposés au risque, produire 20 000 cartes pourrait être la bonne décision. D’ailleurs, produire 10 000 cartes a toujours un écart type de 0 cartes parce que si nous produisons 10 000 cartes, nous les vendrons toujours toutes sans aucun reste.
Remarque : Dans ce classeur, l’option Calcul est définie sur Automatique sauf pour les tables. (Utilisez la commande Calcul dans le groupe Calcul sous l’onglet Formules.) Ce paramètre garantit que notre table de données ne sera pas recalculée, sauf si nous appuyons sur F9, ce qui est une bonne idée, car une table de données volumineuse ralentira votre travail si elle est recalculée chaque fois que vous tapez quelque chose dans votre feuille de calcul. Notez que dans cet exemple, chaque fois que vous appuyez sur F9, le bénéfice moyen change. Cela se produit parce que chaque fois que vous appuyez sur F9, une séquence différente de 1 000 nombres aléatoires est utilisée pour générer des demandes pour chaque quantité de commande.
Intervalle de confiance pour le bénéfice moyen Une question naturelle à se poser dans cette situation est, dans quel intervalle sommes-nous à 95 pour cent sûrs que le vrai profit moyen tombera ? Cet intervalle est appelé intervalle de confiance de 95 % pour le bénéfice moyen. Un intervalle de confiance de 95 % pour la moyenne de toute sortie de simulation est calculé selon la formule suivante :
Dans la cellule J11, vous calculez la limite inférieure pour l’intervalle de confiance de 95 % sur le bénéfice moyen lorsque 40 000 calendriers sont produits avec la formule D13–1,96*D14/RACINE(1000) . Dans la cellule J12, vous calculez la limite supérieure pour notre intervalle de confiance de 95 % avec la formule D13+1,96*D14/RACINE(1000) . Ces calculs sont illustrés dans la figure 60-7.
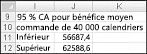
Nous sommes sûrs à 95 pour cent que notre bénéfice moyen lorsque 40 000 calendriers sont commandés est compris entre 56 687 $ et 62 589 $.
-
Un distributeur GMC estime que la demande pour les envoyés de 2005 sera normalement distribuée avec une moyenne de 200 et un écart type de 30. Son coût de réception d’un envoyé est de 25 000 $, et il vend un Envoyé pour 40 000 $. La moitié de tous les Envoyés non vendus au prix plein peut être vendu pour 30 000 $. Il envisage de commander 200, 220, 240, 260, 280 ou 300 envoyés. Combien devrait-il commander ?
-
Un petit supermarché tente de déterminer le nombre d’exemplaires de Personnes magazine qu’ils devraient commander chaque semaine. Ils croient que leur demande de Personnes est régie par la variable aléatoire discrète suivante :
Demande
probabilité
15
0,10
20
0,20
25
0.30
30
0,25
35
0,15
-
Le supermarché paie $1.00 pour chaque copie de Personnes et le vend pour $1.95. Chaque copie invendue peut être retournée au coût de 0,50 $. Combien de copies de Personnes la commande de magasin doit-elle être commandée ?
Vous avez besoin d’une aide supplémentaire ?
Vous pouvez toujours poser des questions à un expert de la Communauté technique Excel ou obtenir une assistance dans la Communauté de support.