Important : Le support pour Office 2016 et Office 2019 a pris fin le 14 octobre 2025. Effectuez une mise à niveau vers Microsoft 365 pour travailler à partir de n’importe quel appareil et continuer à bénéficier du support. Obtenir Microsoft 365
Cet article décrit l’utilisation du Solveur, un programme de complément Microsoft Excel que vous pouvez utiliser pour l’analyse de scénarios, afin de déterminer une combinaison de produits optimale.
Comment puis-je déterminer la combinaison de produits mensuelle qui optimise la rentabilité ?
Les entreprises doivent souvent déterminer la quantité de chaque produit à produire sur une base mensuelle. Dans sa forme la plus simple, le problème de la combinaison de produits implique comment déterminer la quantité de chaque produit qui doit être produit au cours d’un mois afin de maximiser les profits. La combinaison de produits doit généralement respecter les contraintes suivantes :
-
La combinaison de produits ne peut pas utiliser plus de ressources que celles disponibles.
-
La demande pour chaque produit est limitée. Nous ne pouvons pas produire plus d’un produit pendant un mois que la demande le veut, car la production excédentaire est gaspillent (par exemple, un médicament périssable).
Nous allons maintenant résoudre l’exemple suivant de problème de combinaison de produits. Vous trouverez la solution à ce problème dans le fichier Prodmix.xlsx, illustré dans la figure 27-1.
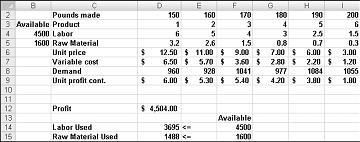
Supposons que nous travaillons pour une société pharmaceutique qui produit six produits différents dans leur usine. La production de chaque produit nécessite de la main-d’œuvre et des matières premières. La ligne 4 de la figure 27-1 montre les heures de travail nécessaires pour produire une livre de chaque produit, et la ligne 5 montre les livres de matière première nécessaires pour produire une livre de chaque produit. Par exemple, la production d’une livre de produit 1 nécessite six heures de travail et 3,2 livres de matière première. Pour chaque médicament, le prix par livre est indiqué dans la ligne 6, le coût unitaire par livre est indiqué dans la ligne 7, et la contribution aux bénéfices par livre est indiquée dans la ligne 9. Par exemple, le produit 2 se vend à 11,00 $ la livre, entraîne un coût unitaire de 5,70 $ la livre et contribue à un bénéfice de 5,30 $ la livre. La demande du mois pour chaque médicament est indiquée dans la ligne 8. Par exemple, la demande pour le produit 3 est de 1 041 livres. Ce mois-ci, 4500 heures de travail et 1 600 livres de matière première sont disponibles. Comment cette entreprise peut-elle maximiser ses bénéfices mensuels ?
Si nous ne connaissions rien au solveur Excel, nous attaquerions ce problème en construisant une feuille de calcul pour suivre les bénéfices et l’utilisation des ressources associées à la combinaison de produits. Ensuite, nous utiliserions l’essai et l’erreur pour varier la combinaison de produits afin d’optimiser le profit sans utiliser plus de main-d’œuvre ou de matière première que ce qui est disponible, et sans produire de médicament en excès de la demande. Nous utilisons solveur dans ce processus uniquement à l’étape d’essai et d’erreur. Essentiellement, solveur est un moteur d’optimisation qui effectue sans problème la recherche d’essai et d’erreur.
Une clé pour résoudre le problème de la combinaison de produits consiste à calculer efficacement l’utilisation des ressources et les bénéfices associés à une combinaison de produits donnée. Un outil important que nous pouvons utiliser pour effectuer ce calcul est la fonction SOMMEPROD. La fonction SOMMEPROD multiplie les valeurs correspondantes dans les plages de cellules et retourne la somme de ces valeurs. Chaque plage de cellules utilisée dans une évaluation SOMMEPROD doit avoir les mêmes dimensions, ce qui implique que vous pouvez utiliser SOMMEPROD avec deux lignes ou deux colonnes, mais pas avec une colonne et une ligne.
À titre d’exemple de la façon dont nous pouvons utiliser la fonction SOMMEPROD dans notre exemple de combinaison de produits, essayons de calculer l’utilisation de nos ressources. Notre utilisation de la main-d’œuvre est calculée par
(Main-d’œuvre utilisée par livre de drogue 1)*(Médicament 1 lb produit)+ (Travail utilisé par livre de drogue 2)*(Médicament 2 livres produits) + ... (Main-d’œuvre utilisée par livre de drogue 6)*(Médicament 6 livres produits)
Nous pourrions calculer l’utilisation du travail de manière plus fastidieuse comme D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. De même, l’utilisation des matières premières peut être calculée en tant que D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Toutefois, la saisie de ces formules dans une feuille de calcul pour six produits prend beaucoup de temps. Imaginez combien de temps cela prendrait si vous travailliez avec une entreprise qui produisait, par exemple, 50 produits dans son usine. Un moyen beaucoup plus facile de calculer l’utilisation de la main-d’œuvre et des matières premières consiste à copier de D14 à D15 la formule SOMMEPROD($D$2 :$I$2,D4 :I4). Cette formule calcule D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (qui est notre utilisation du travail), mais il est beaucoup plus facile d’entrer ! Notez que j’utilise le signe $ avec la plage D2 :I2 de sorte que lorsque je copie la formule, je capture toujours le mélange de produits de la ligne 2. La formule de la cellule D15 calcule l’utilisation des matières premières.
De la même façon, notre bénéfice est déterminé par
(Bénéfice de 1 médicament par livre)*(Médicament 1 livre produit) + (Bénéfice de drogue 2 par livre)*(Drogue 2 livres produites) + ... (Profit de drogue 6 par livre)*(Drogue 6 livres produites)
Le bénéfice est facilement calculé dans la cellule D12 avec la formule SOMMEPROD(D9 :I9,$D$2 :$I$2).
Nous pouvons maintenant identifier les trois composants de notre modèle solveur de combinaison de produits.
-
Cellule cible. Notre objectif est de maximiser les bénéfices (calculés dans la cellule D12).
-
Modification des cellules. Nombre de livres produites par chaque produit (indiqué dans la plage de cellules D2 :I2)
-
Contraintes. Nous avons les contraintes suivantes :
-
N’utilisez pas plus de main-d’œuvre ou de matière première que ce qui est disponible. Autrement dit, les valeurs des cellules D14 :D15 (les ressources utilisées) doivent être inférieures ou égales aux valeurs des cellules F14 :F15 (les ressources disponibles).
-
Ne produisez pas plus d’un médicament que n’est en demande. Autrement dit, les valeurs des cellules D2 :I2 (livres produites par chaque médicament) doivent être inférieures ou égales à la demande pour chaque médicament (répertoriées dans les cellules D8 :I8).
-
Nous ne pouvons pas produire une quantité négative de n’importe quelle drogue.
-
Je vais vous montrer comment entrer la cellule cible, modifier les cellules et les contraintes dans solveur. Ensuite, il vous suffit de cliquer sur le bouton Résoudre pour trouver une combinaison de produits qui optimise les bénéfices !
Pour commencer, cliquez sur l’onglet Données, puis dans le groupe Analyse, cliquez sur Solveur.
Remarque : Comme expliqué dans le chapitre 26, « Présentation de l’optimisation avec le solveur Excel », le solveur est installé en cliquant sur le bouton Microsoft Office, puis sur Options Excel, puis sur Compléments. Dans la liste Gérer, cliquez sur Compléments Excel, case activée la zone Complément solveur, puis cliquez sur OK.
La boîte de dialogue Paramètres du solveur s’affiche, comme illustré dans la figure 27-2.
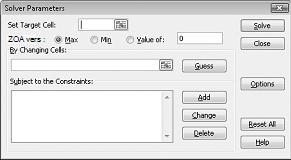
Cliquez sur la zone Définir la cellule cible, puis sélectionnez notre cellule de profit (cellule D12). Cliquez sur la zone En modifiant les cellules, puis pointez sur la plage D2 :I2, qui contient les livres produites par chaque médicament. La boîte de dialogue doit maintenant ressembler à la Figure 27-3.
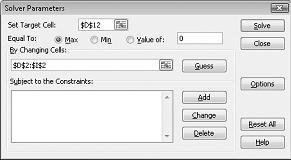
Nous sommes maintenant prêts à ajouter des contraintes au modèle. Cliquez sur le bouton Ajouter. La boîte de dialogue Ajouter une contrainte s’affiche dans la figure 27-4.
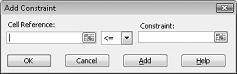
Pour ajouter les contraintes d’utilisation des ressources, cliquez sur la zone Référence de cellule, puis sélectionnez la plage D14 :D15. Sélectionnez <= dans la liste du milieu. Cliquez sur la zone Contrainte, puis sélectionnez la plage de cellules F14 :F15. La boîte de dialogue Ajouter une contrainte doit maintenant ressembler à la figure 27-5.
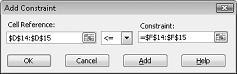
Nous avons maintenant vérifié que lorsque le Solveur essaie différentes valeurs pour les cellules changeantes, seules les combinaisons qui satisfont À la fois D14<=F14 (la main-d’œuvre utilisée est inférieure ou égale à la main-d’œuvre disponible) et D15<=F15 (la matière première utilisée est inférieure ou égale à la matière première disponible) sera prise en compte. Cliquez sur Ajouter pour entrer les contraintes de demande. Renseignez la boîte de dialogue Ajouter une contrainte, comme illustré dans la figure 27-6.
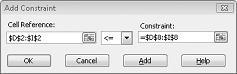
L’ajout de ces contraintes garantit que lorsque le solveur tente différentes combinaisons pour les valeurs de cellule modifiées, seules les combinaisons qui répondent aux paramètres suivants sont prises en compte :
-
D2<=D8 (la quantité produite par le médicament 1 est inférieure ou égale à la demande pour le médicament 1)
-
E2<=E8 (la quantité produite du médicament 2 est inférieure ou égale à la demande de drogue 2)
-
F2<=F8 (la quantité produite du médicament 3 est inférieure ou égale à la demande pour le médicament 3)
-
G2<=G8 (la quantité produite du médicament 4 est inférieure ou égale à la demande de drogue 4)
-
H2<=H8 (la quantité produite du médicament 5 est inférieure ou égale à la demande pour le médicament 5)
-
I2<=I8 (la quantité produite du médicament 6 est inférieure ou égale à la demande pour le médicament 6)
Cliquez sur OK dans la boîte de dialogue Ajouter une contrainte. La fenêtre solveur doit ressembler à la figure 27-7.
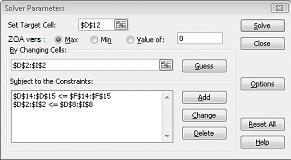
Dans la boîte de dialogue Options du solveur, nous entrerons la contrainte selon laquelle la modification des cellules doit être non négative. Cliquez sur le bouton Options dans la boîte de dialogue Paramètres du solveur. Cochez les cases Supposer le modèle linéaire et Les cases Supposer non négatif, comme illustré dans la figure 27-8 de la page suivante. Cliquez sur OK.
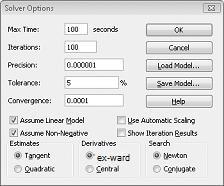
Si vous cochez la case Supposer non négatif, le Solveur prend en compte uniquement les combinaisons de cellules changeantes dans lesquelles chaque cellule changeante suppose une valeur non négative. Nous avons coché la case Supposer un modèle linéaire, car le problème de combinaison de produits est un type spécial de problème solveur appelé modèle linéaire. Essentiellement, un modèle solveur est linéaire dans les conditions suivantes :
-
La cellule cible est calculée en additionnant les termes de la forme (cellule de modification)*(constante).
-
Chaque contrainte satisfait à l'« exigence de modèle linéaire ». Cela signifie que chaque contrainte est évaluée en ajoutant les termes de la forme (cellule de modification)*(constante) et en comparant les sommes à une constante.
Pourquoi ce problème solveur est-il linéaire ? Notre cellule cible (profit) est calculée comme
(Bénéfice de 1 médicament par livre)*(Médicament 1 livre produit) + (Bénéfice de drogue 2 par livre)*(Drogue 2 livres produites) + ... (Profit de drogue 6 par livre)*(Drogue 6 livres produites)
Ce calcul suit un modèle dans lequel la valeur de la cellule cible est dérivée en additionnant les termes de la forme (cellule changeante)*(constante).
Notre contrainte de travail est évaluée en comparant la valeur dérivée de (Travail utilisé par livre de médicament 1)*(Médicament 1 livre produit) + (Travail utilisé par livre de drogue 2)*(Médicament 2 livres produits)+ ... (Travail noused par livre de drogue 6)*(Médicament 6 livres produits) à la main-d’œuvre disponible.
Par conséquent, la contrainte de travail est évaluée en additionnant les termes de la forme (cellule de changement)*(constante) et en comparant les sommes à une constante. La contrainte de travail et la contrainte de matière première répondent toutes deux à l’exigence du modèle linéaire.
Nos contraintes de demande prennent la forme
(Drogue 1 produite)<=(Demande de drogue 1) (Drogue 2 produite)<=(Demande de drogue 2) §(Drogue 6 produite)<=(Demande de drogue 6)
Chaque contrainte de demande répond également à l’exigence du modèle linéaire, car chacune est évaluée en additionnant les termes de la forme (cellule de modification)*(constante) et en comparant les sommes à une constante.
Ayant montré que notre modèle de combinaison de produits est un modèle linéaire, pourquoi devrions-nous nous en soucier ?
-
Si un modèle solveur est linéaire et que nous sélectionnons l’option Supposer un modèle linéaire, le solveur est assuré de trouver la solution optimale pour le modèle solveur. Si un modèle solveur n’est pas linéaire, solveur peut ou non trouver la solution optimale.
-
Si un modèle solveur est linéaire et que nous sélectionnons Le modèle linéaire suppose, le solveur utilise un algorithme très efficace (la méthode simplex) pour trouver la solution optimale du modèle. Si un modèle solveur est linéaire et que nous ne sélectionnons pas Suppose modèle linéaire, le solveur utilise un algorithme très inefficace (méthode GRG2) et peut avoir des difficultés à trouver la solution optimale du modèle.
Après avoir cliqué sur OK dans la boîte de dialogue Options du solveur, nous revenons à la boîte de dialogue solveur main, illustrée plus haut dans la figure 27-7. Lorsque nous cliquons sur Résoudre, solveur calcule une solution optimale (le cas échéant) pour notre modèle de combinaison de produits. Comme je l’ai dit au chapitre 26, une solution optimale au modèle de combinaison de produits serait un ensemble de valeurs de cellules changeantes (livres produites par chaque médicament) qui optimise le profit par rapport à l’ensemble de toutes les solutions possibles. Là encore, une solution réalisable est un ensemble de valeurs de cellule changeantes qui satisfont toutes les contraintes. La modification des valeurs de cellule indiquées dans la figure 27-9 est une solution réalisable, car tous les niveaux de production ne sont pas négatifs, les niveaux de production ne dépassent pas la demande et l’utilisation des ressources ne dépasse pas les ressources disponibles.
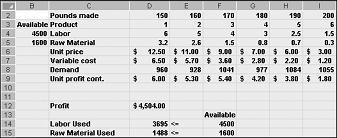
Les valeurs de cellule modifiées indiquées dans la figure 27-10 de la page suivante représentent une solution irréalisable pour les raisons suivantes :
-
Nous produisons plus de médicaments 5 que la demande.
-
Nous utilisons plus de main-d’œuvre que ce qui est disponible.
-
Nous utilisons plus de matière première que ce qui est disponible.
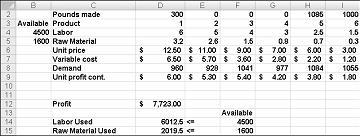
Après avoir cliqué sur Résoudre, le solveur trouve rapidement la solution optimale illustrée dans la figure 27-11. Vous devez sélectionner Conserver la solution du solveur pour conserver les valeurs de solution optimales dans la feuille de calcul.
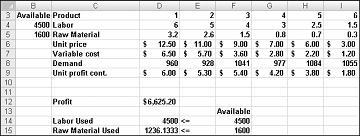
Notre compagnie de médicaments peut maximiser son bénéfice mensuel à un niveau de 6 625,20 $ en produisant 596,67 livres de drogue 4, 1084 livres de drogue 5, et aucun des autres médicaments ! Nous ne pouvons pas déterminer si nous pouvons atteindre le bénéfice maximal de 6 625,20 $ par d’autres moyens. Tout ce dont nous pouvons être sûrs, c’est qu’avec nos ressources limitées et la demande, il n’y a aucun moyen de gagner plus de 6 627,20 $ ce mois-ci.
Supposons que la demande pour chaque produit doit être satisfaite. (Consultez la feuille de calcul No Feasible Solution dans le fichier Prodmix.xlsx.) Nous devons ensuite modifier nos contraintes de demande de D2 :I2<=D8 :I8 à D2 :I2>=D8 :I8. Pour ce faire, ouvrez solveur, sélectionnez la contrainte D2 :I2<=D8 :I8, puis cliquez sur Modifier. La boîte de dialogue Contrainte de modification, illustrée dans la figure 27-12, s’affiche.
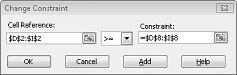
Sélectionnez >=, puis cliquez sur OK. Nous avons maintenant vérifié que le solveur envisagera de modifier uniquement les valeurs de cellule qui répondent à toutes les demandes. Quand vous cliquez sur Résoudre, le message « Le solveur n’a pas trouvé de solution réalisable » s’affiche. Ce message ne signifie pas que nous avons fait une erreur dans notre modèle, mais plutôt qu’avec nos ressources limitées, nous ne pouvons pas répondre à la demande pour tous les produits. Solver nous dit simplement que si nous voulons répondre à la demande pour chaque produit, nous devons ajouter plus de main-d’œuvre, plus de matières premières, ou plus des deux.
Voyons ce qui se passe si nous permettons une demande illimitée pour chaque produit et que nous autorisons la production de quantités négatives de chaque médicament. (Vous pouvez voir ce problème du solveur dans la feuille de calcul Définir les valeurs ne pas converger dans le fichier Prodmix.xlsx.) Pour trouver la solution optimale pour cette situation, ouvrez solveur, cliquez sur le bouton Options, puis désactivez la case à cocher Supposer non négatif. Dans la boîte de dialogue Paramètres du solveur, sélectionnez la contrainte de demande D2 :I2<=D8 :I8, puis cliquez sur Supprimer pour supprimer la contrainte. Lorsque vous cliquez sur Résoudre, le solveur renvoie le message « Définir les valeurs de cellule ne convergent pas ». Ce message signifie que si la cellule cible doit être agrandie (comme dans notre exemple), il existe des solutions possibles avec des valeurs de cellules cibles arbitrairement grandes. (Si la cellule cible doit être réduite, le message « Définir les valeurs de cellule ne convergent pas » signifie qu’il existe des solutions possibles avec des valeurs de cellules cibles arbitrairement petites.) Dans notre situation, en autorisant la production négative d’un médicament, nous « créons » des ressources qui peuvent être utilisées pour produire arbitrairement de grandes quantités d’autres drogues. Compte tenu de notre demande illimitée, cela nous permet de faire des profits illimités. Dans une situation réelle, nous ne pouvons pas faire une somme infinie d’argent. En bref, si vous voyez « Définir les valeurs ne convergent pas », votre modèle a une erreur.
-
Supposons que notre société pharmaceutique peut acheter jusqu’à 500 heures de travail à 1 $ de plus par heure que les coûts actuels de main-d’œuvre. Comment pouvons-nous maximiser les profits ?
-
Dans une usine de fabrication de puces, quatre techniciens (A, B, C et D) produisent trois produits (produits 1, 2 et 3). Ce mois-ci, le fabricant de puces peut vendre 80 unités de Produit 1, 50 unités de Produit 2 et au plus 50 unités de Produit 3. Le technicien A peut fabriquer uniquement les produits 1 et 3. Le technicien B peut fabriquer uniquement les produits 1 et 2. Le technicien C peut fabriquer uniquement le produit 3. Le technicien D peut fabriquer uniquement le produit 2. Pour chaque unité produite, les produits contribuent au bénéfice suivant : Produit 1, 6 $ ; Produit 2, 7 $ ; et Produit 3, 10 $. Le temps (en heures) dont chaque technicien a besoin pour fabriquer un produit est le suivant :
Produit
Technicien A
Technicien B
Technicien C
Technicien D
1
2
2,5
Impossible de faire
Impossible de faire
2
Impossible de faire
3
Impossible de faire
3,5
3
3
Impossible de faire
4
Impossible de faire
-
Chaque technicien peut travailler jusqu’à 120 heures par mois. Comment le fabricant de puces peut-il maximiser ses bénéfices mensuels ? Supposons qu’un nombre fractionnaire d’unités puisse être produit.
-
Une usine de fabrication d’ordinateurs produit des souris, des claviers et des joysticks de jeux vidéo. Le bénéfice par unité, l’utilisation du travail unitaire, la demande mensuelle et l’utilisation du temps machine par unité sont indiqués dans le tableau suivant :
Souris
Claviers
Joysticks
Profit/unité
8 $
11 $
9 $
Utilisation de la main-d’œuvre/unité
.2 heures
.3 heures
.24 heures
Temps/unité de la machine
.04 heure
.055 heure
.04 heure
Demande mensuelle
15 000
27,000
11,000
-
Chaque mois, un total de 13 000 heures de travail et 3 000 heures de temps machine sont disponibles. Comment le fabricant peut-il maximiser sa contribution aux bénéfices mensuels de l’usine ?
-
Résolvez notre exemple de médicament en supposant qu’une demande minimale de 200 unités pour chaque médicament doit être satisfaite.
-
Jason fait des bracelets en diamant, des colliers et des boucles d’oreilles. Il veut travailler un maximum de 160 heures par mois. Il a 800 onces de diamants. Le profit, le temps de travail et les onces de diamants nécessaires pour produire chaque produit sont donnés ci-dessous. Si la demande pour chaque produit est illimitée, comment Jason peut-il maximiser ses profits ?
Produit
Bénéfice unitaire
Heures de travail par unité
Onces de diamants par unité
Bracelet
300 €
.35
1,2
Collier
200 $
.15
0,75
Boucles
100 €
0,05
0,5










