LINEST (opis funkcije)

Opis

Funkcija LINEST izračunava statistiku za pravac korištenjem metode "najmanji kvadrati" za izračun ravnog pravca koji najbolje odgovara vašim podacima, a potom vraća polje koje opisuje taj pravac. Također možete kombinirati funkciju LINEST s drugim funkcijama da biste izračunali statistiku za druge vrste modela koji su linearni s nepoznatim parametrima, uključujući serije polinoma, logaritamske, eksponencijalne i potencijske serije. Budući da ova funkcija vraća polje vrijednosti, potrebno ju je unijeti kao formulu polja. Upute slijede primjere u ovom članku.

Jednadžba pravca je:

y = mx + b

– ili –

y = m1x1 + m2x2 + ... + b

ako postoji više raspona vrijednosti x, pri čemu su zavisne vrijednosti y funkcija nezavisnih vrijednosti x. Vrijednosti m koeficijenti su koji odgovaraju svakoj vrijednosti x, a b je konstantna vrijednost. Upamtite da y,x i m mogu biti vektori. Polje koje vraća funkcija LINEST je {mn;mn-1;...;m1;b}. LINEST također može vratiti dodatne regresijske statistike.

Sintaksa

LINEST(poznati_y; [poznati_x]; [konst]; [stat])

Sintaksa funkcije LINEST sadrži sljedeće argumente:

Sintaksa

• poznati_y    Obavezno. Skup vrijednosti y koje su vam već poznate u odnosu y = mx + b.

  • Ako je raspon poznati_y u jednom stupcu, svaki stupac u skupu poznati_x tumači se kao zasebna varijabla.

  • Ako je raspon skupa poznati_y sadržan u jednom retku, svaki redak skupa poznati_x tumači se kao zasebna varijabla.

• poznati_x    Obavezno. Skup vrijednosti x koje su vam već poznate u odnosu y = mx + b.

  • Raspon poznati_x može obuhvaćati jedan ili više skupova varijabli. Ako se koristi samo jedna varijabla, poznati_y i poznati_x mogu biti rasponi bilo kojeg oblika, tako dugo dok su im dimenzije jednake. Ako se koristi više od jedne varijable, poznati_y mora biti vektor (odnosno raspon s visinom jednog retka ili širinom jednog stupca).

  • Ako se poznati_x izostavi, pretpostavlja se da je riječ o polju {1,2,3,...} iste veličine kao i poznati_y.

• konst    Dodatno. Logička vrijednosti koja određuje hoće li konstanta b biti jednaka 0.

  • Ako je vrijednost konstTRUE ili je izostavljena, b se izračunava normalnim putem.

  • Ako je vrijednost konst je FALSE, određuje se da je b jednak 0, a vrijednosti m prilagođavaju se da bi odgovarale y = mx.

• stat    Dodatno. Logička vrijednost koja određuje hoće li biti vraćene i dodatne statistike regresije.

  • Ako je statistika TRUE, LINEST vraća dodatnu statistiku regresije. rezultat je vraćeno polje {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r²,sey; F,df;ssreg,ssresid}.

  • Ako je stat FALSE ili je izostavljen, LINEST vraća samo m-koeficijente i konstantu b.

    Dodatni statistički podaci regresije su sljedeći.

Sljedeća ilustracija prikazuje redoslijed kojim se vraćaju dodatni statistički podaci.

Primjedbe

• Bilo koji pravac možete opisati pomoću nagiba i sjecišta osi y.

  Nagib (m):
  Da biste pronašli nagib crte, često napisan kao m, uzmite dvije točke na crti (x1,y1) i (x2,y2); nagib je jednak (y2 - y1)/(x2 - x1).

  Y-intercept (b):
  Y-presretanje retka, često napisano kao b, vrijednost je y na mjestu gdje crta prelazi os y.

  Jednadžba pravca je y = mx + b. Kada su vam poznate vrijednosti m i b, možete izračunati bilo koju točku na pravcu tako da u jednadžbu uvrstite vrijednost y ili vrijednost x. Također možete koristiti funkciju TREND.

• Kad imate samo jednu nezavisnu varijablu x, nagib (m) i sjecište osi y (b) možete odrediti pomoću sljedećih formula:

  Nagib:
  =INDEX(LINEST(known_y's;known_x's),1)

  Presretanje Y:
  =INDEX(LINEST(known_y's,known_x's),2)

• Točnost pravca izračunatog pomoću funkcije LINEST ovisi o stupnju raspršenosti podataka. Što su podaci linearniji, to je model LINEST točniji. LINEST koristi metodu najmanjih kvadrata za izračunavanje pravca koji najbolje odgovara podacima. Ako imate samo jednu neovisnu varijablu x, izračuni za m i b temelje se na sljedećim formulama:

  

  

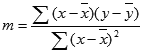
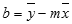
  pri čemu su x i y aritmetičke sredine uzorka, odnosno x = AVERAGE(poznati_ x) i y = AVERAGE(poznati_y).

• Funkcije line- and curve-fitting LINEST i LOGEST mogu izračunati najbolju ravnu ili eksponencijalnu krivulju koja odgovara vašim podacima. No morate odlučiti koji od ta dva rezultata najbolje odgovara vašim podacima. Trend( known_y,known_x ) možete izračunati za ravnu crtu ili GROWTH(known_y,known_x)za eksponencijalnu krivulju. Te funkcije, bez argumenta new_x, vraćaju polje vrijednosti y predviđenih duž te crte ili krivulje na stvarnim točkama podataka. Zatim možete usporediti predviđene vrijednosti sa stvarnim vrijednostima. Da biste ih mogli uspoređivati, možete ih i ucrt ati.

• U regresijskoj analizi Excel za svaku točku izračunava kvadrat razlike između vrijednosti y procijenjene za tu točku i njezine stvarne vrijednosti y. Zbroj kvadrata tih razlika naziva se rezidualnim zbrojem kvadrata, odnosno ssresid. Excel tada izračunava ukupni zbroj kvadrata, odnosno sstotal. Kada je argument konst = TRUE ili je izostavljen, ukupni zbroj kvadrata zbroj je kvadrata razlika između stvarnih vrijednost y i prosjeka vrijednosti y. Kada je argument konst = FALSE, ukupni zbroj kvadrata je zbroj kvadrata stvarnih vrijednosti y (bez oduzimanja prosječne vrijednosti y od svake pojedine vrijednosti y). Regresijski zbroj kvadrata, ssreg, moguće je dobiti iz jednadžbe ssreg = sstotal - ssresid. Manji rezidualni zbroj kvadrata uspoređuje se s ukupnim zbrojem kvadrata, što je veća vrijednost koeficijenta određivanja, r^2,što je pokazatelj uspješnosti jednadžbe koja je rezultat regresijske analize, objašnjava odnos među varijablama. Vrijednost r^{2 jednako} je ssreg/sstotal.

• U nekim slučajevima jedan ili više stupaca X (pretpostavljaju da su stupci Y i X u stupcima) možda neće imati dodatne prediktivne vrijednosti u prisutnosti drugih stupaca X. Drugim riječima, uklanjanje jednog ili više stupaca X može dovesti do predviđenih vrijednosti Y koje su jednako točne. U tom slučaju ti suvišni stupci X moraju se izostaviti iz modela regresije. Taj se fenomen naziva "collinearity" jer se bilo koji suvišni stupac X može izraziti kao zbroj višekratnih brojeva stupaca X koji nisu suvišni. Funkcija LINEST provjerava kolinearnost i uklanja sve suvišne stupce X iz regresijnog modela kada ih identificira. Uklonjeni stupci X mogu se prepoznati u izlazu LINEST kao da imaju 0 koeficijenta uz 0 se vrijednosti. Ako se jedan ili više stupaca ukloni kao suvišan, to utječe na df jer df ovisi o broju stupaca X koji se zapravo koriste u prediktivne svrhe. Detalje o izračunu df-a potražite u primjeru 4. Ako se df promijeni jer su uklonjeni suvišni stupci X, utječu se i vrijednosti sey i F. Kolinearnost bi u praksi trebala biti relativno rijetka. No jedan je slučaj u kojem je vjerojatnije da će se pojaviti kada neki stupci X sadrže samo 0 i 1 vrijednosti kao pokazatelje je li predmet u eksperimentu član određene grupe ili nije. Ako je const = TRUE ili je izostavljena, funkcija LINEST učinkovito umeće dodatni stupac X od svih 1 vrijednosti za modeliranje presretanja. Ako imate stupac s 1 za svaki predmet ako je muško ili 0, a imate stupac s 1 za svaki predmet ako je ženski ili 0 ako nije, taj je potonji stupac suvišan jer se unosi u njemu mogu dobiti oduzimanjem unosa u stupcu "muški pokazatelj" od unosa u dodatni stupac svih 1 vrijednosti koje dodaje funkcija LINEST.

• Vrijednost df izračunava se kako slijedi ako se stupci X ne uklanjanju iz modela zbog kolinearnosti: ako postoje stupci k s varijablama poznati_x i konst = TRUE ili izostavljen, df = n – k – 1. Ako je konst = FALSE, df = n - k. U oba slučaja, svaki stupac X koji je uklonjen zbog kolinearnosti povećava vrijednost varijable df za 1.

• Pri unosu konstante polja (primjerice poznati_x) kao argumenta, koristite zareze da biste odvojili vrijednosti sadržane u istom redu i točke sa zarezom da biste odvojili retke. Znakovi razdjelnika ovise o regionalnim postavkama.

• Primijetite da vrijednosti y predviđene jednadžbom regresije ne moraju biti valjane ako su izvan raspona vrijednosti y upotrijebljenih prilikom definiranja jednadžbe.

• Algoritam u osnovi funkcije LINEST razlikuje se od algoritma koji se koristi za funkcije SLOPE i INTERCEPT. Razlika između ovih algoritama može dovesti do različitih rezultata ako su podaci neodređeni i kolinearni. Ako su, primjerice, točke podataka argumenta poznati_y 0 te ako su točke podataka argumenta poznati_x 1:

  • LINEST vraća vrijednost 0. Algoritam funkcije LINEST dizajniran je za vraćanje razumnih rezultata za kolinearne podatke te je, u ovom slučaju, moguće pronaći barem jedan odgovor.

  • SLOPE i INTERCEPT vraćaju #DIV/0! pogreška. Algoritam funkcija SLOPE iINTERCEPT namijenjen je samo jednom odgovoru, a u ovom slučaju može biti više odgovora.

• Osim korištenja funkcije LOGEST za izračun statistike za druge vrste regresije, možete koristiti funkciju LINEST za izračun raspona drugih vrsta regresije unosom funkcija varijabli x i y kao nizova x i y za funkciju LINEST. Primjerice, sljedeća formula:

  =LINEST(yvrijednosti; xvrijednosti^COLUMN($A:$C))

  funkcionira kad imate jedan stupac vrijednosti y i jedan stupac vrijednosti x za izračun kubne (polinom 3. reda) aproksimacije oblika:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Ovu formulu možete prilagoditi za izračun drugih vrsta regresije, ali u nekim slučajevima bit će potrebno usklađivanje izlaznih vrijednosti i ostalih statističkih podataka.

• Vrijednost F-testa koju vraća funkcija LINEST razlikuje se od vrijednosti F-testa koju vraća funkcija FTEST. LINEST vraća F statistiku, a FTEST vjerojatnost.

Primjeri