Hogyan határozhatja meg egy vállalat a Solver használatával, hogy milyen projekteket kell végrehajtania?
Minden évben egy olyan cégnek, mint Eli Lilly, meg kell határoznia, hogy mely gyógyszereket kell fejlesztenie; egy olyan vállalat, mint a Microsoft, mely szoftverprogramokat fejlesztenek; egy olyan cég, mint a Proctor & Gamble, amely új fogyasztói termékeket fejleszt. Az Excel Solver funkciója segíthet a vállalatnak a döntések meghozatalában.
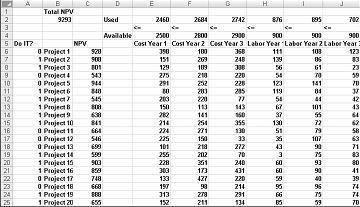
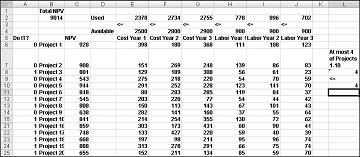
A legtöbb vállalat olyan projekteket szeretne megvalósítani, amelyek a legnagyobb nettó jelenértéket (NPV) hozzájárulnak, korlátozott erőforrások (általában tőke és munkaerő) függvényében. Tegyük fel, hogy egy szoftverfejlesztő vállalat megpróbálja meghatározni, hogy 20 szoftverprojekt közül melyiket kell elvégeznie. Az NPV (több millió dollárban) az egyes projektek által járult hozzá, valamint a tőke (több millió dollárban) és a programozók száma a következő három év mindegyikében a Capbudget.xlsx fájl Alapmodell munkalapján található, amely a következő oldalon, a 30-1. ábrán látható. A Project 2 például 908 millió dollárt ad. 151 millió dollárt igényel az 1. év során, 269 millió dollárt a 2. évben, és 248 millió dollárt a 3. évben. A 2. projekthez 139 programozóra van szükség az 1. év során, 86 programozót a 2. évben és 83 programozót a 3. évben. Az E4:G4 cellák a három év alatt rendelkezésre álló tőkét (millió dollárban) mutatják, a H4:J4 cellák pedig azt jelzik, hogy hány programozó érhető el. Például az 1. év alatt akár 2,5 milliárd dollárnyi tőke és 900 programozó áll rendelkezésre.
A vállalatnak el kell döntenie, hogy vállalja-e az egyes projekteket. Tegyük fel, hogy nem tudjuk vállalni a szoftverprojektek töredékét; ha a szükséges erőforrások közül 0,5-öt foglalnánk le, például lenne egy nem működő programunk, amely 0 USD bevételt hozna nekünk!
A modellezési helyzetekben az a trükk, hogy bináris változó cellákat használ, vagy nem tesz valamit. A bináris változó cella értéke mindig 0 vagy 1. Ha egy projektnek megfelelő bináris változó cella értéke 1, akkor a projektet hajtjuk létre. Ha egy projektnek megfelelő bináris változó cella értéke 0, akkor nem a projektet hajtjuk létre. A Solver úgy van beállítva, hogy egy korlátozás hozzáadásával bináris változócellák tartományát használja – jelölje ki a használni kívánt változó cellákat, majd válassza a Bin elemet a Kényszer hozzáadása párbeszédpanel listájából.
Ezzel a háttérrel készen állunk a szoftverprojekt kiválasztásával kapcsolatos probléma megoldására. A Solver-modellhez hasonlóan a célcella, a változó cellák és a korlátozások azonosításával kezdjük.
-
Célcella. Maximalizáljuk a kiválasztott projektek által létrehozott NPV-t.
-
Cellák módosítása. Minden projekthez egy 0 vagy 1 bináris változócellát keresünk. Ezeket a cellákat az A6:A25 tartományban találtam (és a tartomány neve doit). Például az A6 cellában lévő 1 azt jelzi, hogy az 1. projektet vállaljuk; A C6 cellában lévő 0 azt jelzi, hogy nem vállaljuk az 1. projektet.
-
Korlátok. Meg kell győződnünk arról, hogy minden t. év (t=1, 2, 3) esetében a felhasznált t. év tőkéje kisebb vagy egyenlő, mint a Rendelkezésre álló év t tőkéje, és a t. év felhasznált munka értéke kisebb vagy egyenlő, mint a Rendelkezésre álló év t munka.
Amint látható, munkalapunknak ki kell számítania a projektek tetszőleges kiválasztásához az NPV-t, az évente felhasznált tőkét és az évente használt programozókat. A B2 cellában a SZORZATÖSSZEG(doit,NPV) képletet használom a kijelölt projektek által létrehozott teljes NPV kiszámításához. (Az NPV tartománynév a C6:C25 tartományra hivatkozik.) Minden olyan projekt esetében, amelynek az A oszlopában 1 van, ez a képlet felveszi a projekt NMÉ-ét, és minden olyan projekt esetében, amelynek az A oszlopában 0 van, ez a képlet nem veszi fel a projekt NMÉ-ét. Ezért az összes projekt NMÉ-jének kiszámítására képesek vagyunk, a célcella pedig lineáris, mert az űrlapot követő kifejezések összegzésével történik (változó cella)*(állandó). Hasonló módon számítom ki az évente felhasznált tőkét és az évente felhasznált munkát úgy, hogy az E2-ből az F2:J2-be másolja a SUMPRODUCT(doit,E6:E25) képletet.
Most kitöltöm a Solver paraméterei párbeszédpanelt a 30-2. ábrán látható módon.
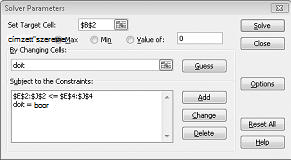
Célunk a kijelölt projektek NMÉ-jének maximalizálása (B2 cella). A változó cellák (a doit nevű tartomány) az egyes projektek bináris változó cellái. Az E2:J2<=E4:J4 kényszer biztosítja, hogy a felhasznált tőke és munka minden évben kisebb vagy egyenlő legyen a rendelkezésre álló tőkével és munkaerővel. Ha a változó cellákat binárissá tevő kényszert szeretné hozzáadni, kattintson a Hozzáadás gombra a Solver paraméterei párbeszédpanelen, majd válassza a Doboz lehetőséget a párbeszédpanel közepén található listából. A Kényszer hozzáadása párbeszédpanelnek a 30-3. ábrán látható módon kell megjelennie.
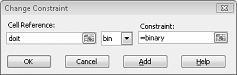
A modell lineáris, mert a célcella az űrlapot (változó cellát)*(állandót) tartalmazó kifejezések összegeként van kiszámítva, és mivel az erőforrás-használati korlátozások kiszámítása a (változó cellák)*(állandók) összegének konstanssal való összehasonlításával történik.
Ha a Solver paraméterei párbeszédpanel ki van töltve, kattintson a Solve (Megoldás) gombra, és az eredmények a 30-1. ábrán láthatók. A vállalat a 2., 3., 6–10., 14–16., 19. és 20. projektek kiválasztásával legfeljebb 9293 millió DOLLÁR (9,293 milliárd USD) nettó nettó jelenértékhez juthat.
A projektkijelölési modellek néha más korlátozásokkal is rendelkeznek. Tegyük fel például, hogy ha a Project 3-at választjuk, akkor a Project 4-et is ki kell választanunk. Mivel a jelenlegi optimális megoldás a Project 3-at választja, a Project 4-et nem, tudjuk, hogy a jelenlegi megoldás nem maradhat optimális. A probléma megoldásához egyszerűen adja hozzá azt a korlátozást, hogy a Project 3 bináris változócellája kisebb vagy egyenlő a Project 4 bináris változócellájának értékével.
Ezt a példát a fájl Capbudget.xlsx Ha 3, majd 4 munkalapján találja, amely a 30-4. ábrán látható. Az L9 cella a Project 3-hoz kapcsolódó bináris értékre, az L12 cellára pedig a Project 4-höz kapcsolódó bináris értékre utal. Az L9<=L12 kényszer hozzáadásával, ha a Project 3-at választjuk, az L9 értéke 1, a kényszer pedig az L12-t (a Project 4 bináris fájlját) 1-nek kényszeríti. Ha nem választjuk ki a Project 3-at, a kényszernek a Project 4 változó cellájában is korlátozás nélkül kell hagynia a bináris értéket. Ha nem a Project 3-at választjuk, akkor az L9 értéke 0, a kényszerünk pedig lehetővé teszi, hogy a Project 4 bináris fájlja 0 vagy 1 legyen, és ez az, amit szeretnénk. Az új optimális megoldás a 30-4. ábrán látható.
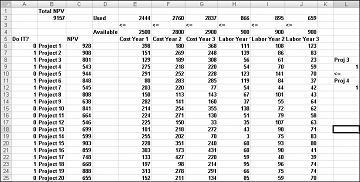
Egy új optimális megoldást akkor számítunk ki, ha a Project 3 kiválasztása azt jelenti, hogy a Project 4-et is ki kell választanunk. Most tegyük fel, hogy csak négy projektet tudunk végrehajtani az 1–10. projektek közül. (Lásd a P1–P10-ből legfeljebb 4 munkalapot, amely a 30–5. ábrán látható.) Az L8 cellában kiszámítjuk az 1–10. projektekhez társított bináris értékek összegét a SZUM(A6:A15) képlettel. Ezután hozzáadjuk az L8<=L10 kényszert, amely biztosítja, hogy az első 10 projektből legfeljebb 4 van kiválasztva. Az új optimális megoldás a 30-5. ábrán látható. Az NPV 9,014 milliárd dollárra csökkent.
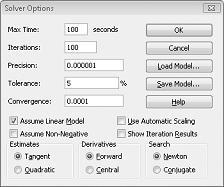
A lineáris solver-modellek, amelyekben néhány vagy az összes változó cellának binárisnak vagy egész számnak kell lennie, általában nehezebb megoldani, mint a lineáris modelleket, amelyekben minden változó cella törtként szerepelhet. Emiatt gyakran elégedettek vagyunk a bináris vagy egész számok programozásával kapcsolatos problémák közel optimális megoldásával. Ha a Solver-modell hosszú ideig fut, érdemes lehet módosítani a Tűrés beállítást a Solver beállításai párbeszédpanelen. (Lásd a 30–6. ábrát.) A 0,5%-os tűrésbeállítás például azt jelenti, hogy a Solver leáll, amikor első alkalommal talál olyan megvalósítható megoldást, amely az elméleti optimális célcella értékének 0,5 százalékán belül van (az elméleti optimális célcellaérték az optimális célérték, amelyet akkor talál, amikor a bináris és egész számra vonatkozó korlátozásokat nem adja meg). Gyakran szembesülünk azzal a döntéssel, hogy 10 percen belül választ találunk az optimális 10 százalékon belül, vagy optimális megoldást találunk két hét múlva a számítógép előtt! Az alapértelmezett tűrésérték 0,05%, ami azt jelenti, hogy a Solver leáll, ha az elméleti optimális célcella értékének 0,05 százalékán belül talál célcellaértéket.
-
Egy vállalatnak kilenc projektje van. Az egyes projektek által hozzáadott nettó jelenérték és az egyes projektek által a következő két évben szükséges tőke az alábbi táblázatban látható. (Minden szám milliós.) Az 1. projekt például 14 millió USD NPV-t ad hozzá, és 12 millió usd kiadást igényel az 1. év során és 3 millió usd-t a 2. évben. Az 1. év során 50 millió dollár tőke áll rendelkezésre a projektekhez, és 20 millió dollár áll rendelkezésre a 2. év során.
|
NMÉ |
1. év kiadásai |
2. év kiadásai |
|
|---|---|---|---|
|
1. projekt |
14 |
12 |
3 |
|
2. projekt |
17 |
54 |
7 |
|
3. projekt |
17 |
6 |
6 |
|
4. projekt |
15 |
6 |
2 |
|
5. projekt |
40 |
30 |
35 |
|
Project 6 |
12 |
6 |
6 |
|
Project 7 |
14 |
48 |
4 |
|
Project 8 |
10 |
36 |
3 |
|
Project 9 |
12 |
18 |
3 |
-
Ha nem tudjuk vállalni egy projekt töredékét, de vagy az összeset vagy egyiket sem kell vállalnunk, hogyan maximalizálhatjuk az NPV-t?
-
Tegyük fel, hogy a Project 4 esetében az 5. projektet kell elvégezni. Hogyan maximalizálhatjuk az NPV-t?
-
Egy kiadó cég próbálja meghatározni, hogy melyik 36 könyvet kell kiadnia ebben az évben. A Pressdata.xlsx fájl az alábbi információkat tartalmazza az egyes könyvekről:
-
Előre jelzett bevételi és fejlesztési költségek (több ezer dollárban)
-
Az egyes könyvek oldalai
-
Hogy a könyv a szoftverfejlesztők közönsége felé irányul-e (az E oszlopban egy 1-et jelöl)
Egy kiadó cég évente legfeljebb 8500 oldalt tartalmazó könyveket tehet közzé, és legalább négy, szoftverfejlesztőknek ajánlott könyvet kell közzétennie. Hogyan maximalizálhatja a vállalat nyereségét?
-
Ez a cikk Wayne L. Winston Microsoft Office Excel 2007 Adatelemzés és üzleti modellezés című cikkéből származik.
Ez az osztálytermi stílusú könyv Wayne Winston, egy jól ismert statisztikus és üzleti professzor előadássorozatából készült, aki az Excel kreatív, gyakorlati alkalmazásaira specializálódott.










