Fontos: 2025. október 14-én véget ér az Office 2016 és az Office 2019 támogatása. Frissítsen most a Microsoft 365-re, hogy bármilyen eszközről dolgozni tudjon, és továbbra is támogatáshoz juthasson. A Microsoft 365 beszerzése
Ez a cikk a Solver, a lehetőségelemzéshez használható Microsoft Excel-bővítményprogram használatát ismerteti az optimális termékkeverés meghatározásához.
Hogyan határozhatom meg a jövedelmezőséget maximalizáló havi termékkeveréseket?
A vállalatoknak gyakran meg kell határozniuk, hogy az egyes termékek mennyisége havi alapon készüljön. Legegyszerűbb formájában a termék mix problémája magában foglalja, hogyan kell meghatározni az egyes termékek mennyiségét, amelyeket egy hónap alatt kell előállítani a nyereség maximalizálása érdekében. A termékkeveréknek általában meg kell felelnie a következő korlátozásoknak:
-
A termékkeverés nem használhat több erőforrást, mint amennyi rendelkezésre áll.
-
Az egyes termékekre korlátozott igény van. Nem tudunk több terméket előállítani egy hónap alatt, mint amennyit a kereslet diktál, mert a felesleges termelés elpazarolódik (például egy romlandó gyógyszer).
Most oldjuk meg a következő példát a termékkeverési problémára. A probléma megoldását a 27-1. ábrán látható Prodmix.xlsx fájlban találja.
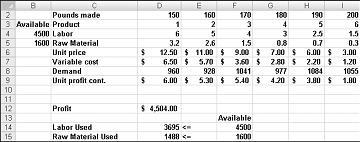
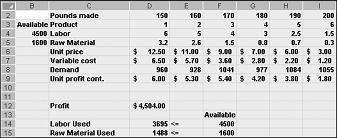
Tegyük fel, hogy egy drogcégnek dolgozunk, amely hat különböző terméket gyárt az üzemükben. Minden termék előállításához munkaerő és nyersanyag szükséges. A 27-1. ábrán a 4. sor az egyes termékek egy fontjának előállításához szükséges munkaórákat, az 5. sorban pedig az egyes termékek egy fontjának előállításához szükséges nyersanyagot mutatja. Az 1. termék kilójának előállításához például hat óra munka és 3,2 font nyersanyag szükséges. Minden gyógyszer esetében a fontonkénti ár a 6. sorban, a fontonkénti egységköltség a 7. sorban, a fontonkénti nyereség pedig a 9. sorban van megadva. A 2. termék például 11,00 USD/fontért értékesít, 5,70 USD/font egységköltséggel jár, és 5,30 USD nyereséget ad ki fontonként. Az egyes gyógyszerekre vonatkozó havi kereslet a 8. sorban van megadva. A 3. termék iránti kereslet például 1041 font. Ebben a hónapban 4500 óra munka és 1600 font nyersanyag áll rendelkezésre. Hogyan maximalizálhatja a vállalat a havi nyereségét?
Ha nem tudunk semmit az Excel Solverről, akkor ezt a problémát úgy támadjuk meg, hogy létrehozunk egy munkalapot, amely nyomon követi a termékkeveréssel társított nyereséget és erőforrás-használatot. Ezután a próbaverziót és a hibát használnánk, hogy módosítsuk a termékkeveréket, hogy optimalizáljuk a nyereséget anélkül, hogy több munkaerőt vagy nyersanyagot használnánk, mint amennyi rendelkezésre áll, és anélkül, hogy bármilyen, a keresletet meghaladó gyógyszert termelnénk. Ebben a folyamatban a Solvert csak a próba- és hibaszakaszban használjuk. A Solver lényegében egy optimalizálási motor, amely hibátlanul hajtja végre a próba- és hibakeresést.
A termékkeveréssel kapcsolatos probléma megoldásának egyik kulcsa, hogy hatékonyan számítsa ki az adott termékkeveréssel járó erőforrás-használatot és nyereséget. Ennek a számításnak egy fontos eszköze a SZORZATÖSSZEG függvény. A SZORZATÖSSZEG függvény összeszorozza a cellatartományok megfelelő értékeit, és visszaadja ezeknek az értékeknek az összegét. Az SZORZATÖSSZEG kiértékelése során használt cellatartományoknak azonos dimenziókkal kell rendelkezniük, ami azt jelenti, hogy két vagy két sorból álló SZORZATÖSSZEG használhat, egy oszloppal és egy sorral azonban nem.
A SZORZATÖSSZEG függvény termékkeverés példában való használatának példájaként próbáljuk kiszámolni az erőforrás-használatot. A munkaerő-használatot a következő alapján számítjuk ki:
(Felhasznált munka fontonként kábítószer 1)*(Drog 1 font termelve)+ (Munka felhasznált egy font kábítószer 2)*(Kábítószer 2 font előállított) + ... (Munka felhasznált egy font kábítószer 6)*(Kábítószer 6 font előállított)
A munkaerő-használatot egyszerűbben is kiszámíthatjuk, mint D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Hasonlóképpen, a nyersanyag-felhasználás a következőképpen számítható ki: D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. A képletek hat termék munkalapra való beírása azonban időigényes feladat. Képzelje el, mennyi időbe telne, ha egy olyan céggel dolgozna, amely például 50 terméket állít elő az üzemében. A munkaerő- és nyersanyag-felhasználás kiszámításának sokkal egyszerűbb módja, ha a D14-ből a D15-be másolja a SZORZATÖSSZEG($D$2:$I$2,D4:I4)) képletet. Ez a képlet kiszámítja a D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (ami a munkaerő-használatunk) számítását, de sokkal könnyebb belépni! Figyelje meg, hogy a $ jelet a D2:I2 tartománnyal használom, így a képlet másolásakor még mindig rögzítem a 2. sorból származó termékkeveréket. A D15 cellában lévő képlet kiszámítja a nyersanyag-felhasználást.
Hasonló módon a nyereséget a
(Gyógyszer 1 nyereség fontonként)*(Drog 1 font termelve) + (Gyógyszer 2 nyereség fontonként)*(Drog 2 font termelve) + ... (Gyógyszer 6 nyereség fontonként)*(Drog 6 font termelve)
A nyereség könnyen kiszámítható a D12 cellában a SZORZATÖSSZEG(D9:I9,$D$2:$I$2) képlettel.
Most már azonosíthatjuk a termékkeverésű Solver-modell három összetevőjét.
-
Célcella. Célunk a nyereség maximalizálása (a D12 cellában számítva).
-
Cellák módosítása. Az egyes termékekből előállított fontok száma (a D2:I2 cellatartományban szerepel)
-
Korlátok. A következő korlátozások vannak bennünk:
-
Ne használjon több munkaerőt vagy nyersanyagot, mint amennyi rendelkezésre áll. Ez azt jelzi, hogy a D14:D15 cellában (a felhasznált erőforrásokban) lévő értékeknek kisebbnek vagy egyenlőnek kell lenniük az F14:F15 cellában lévő értékekkel (a rendelkezésre álló erőforrásokkal).
-
Ne termelnek több gyógyszert, mint a kereslet. Ez azt jelzi, hogy a D2:I2 (az egyes gyógyszerekből előállított font) cellákban lévő értékeknek kisebbnek vagy egyenlőnek kell lenniük az egyes gyógyszerek iránti igénynél (a D8:I8 cellákban).
-
Nem tudunk negatív mennyiségű gyógyszert előállítani.
-
Bemutatom, hogyan adhatja meg a célcellát, módosíthatja a cellákat és a korlátozásokat a Solverben. Ezután mindössze annyit kell tennie, hogy a Solve gombra kattint, hogy megtalálja a profit-maximalizáló termék mix!
Először kattintson az Adatok fülre, majd az Elemzés csoportban a Solver elemre.
Megjegyzés: A 26. fejezetben ismertetett "Bevezetés az optimalizálásba az Excel Solverrel" című fejezetben leírtak szerint a Solver telepítése a Microsoft Office gombra, majd az Excel beállításai, majd a bővítmények elemre kattintva történik. A Kezelés listában kattintson az Excel-bővítmények elemre, jelölje be a Solver bővítmény jelölőnégyzetet, majd kattintson az OK gombra.
Megjelenik a Solver paraméterei párbeszédpanel, ahogy a 27–2. ábrán is látható.
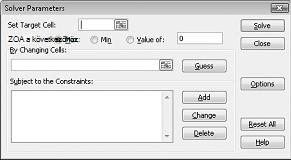
Kattintson a Célcella beállítása mezőre, majd jelölje ki a nyereségcellát (D12 cellát). Kattintson a Cellák módosításával mezőre, majd mutasson a D2:I2 tartományra, amely az egyes gyógyszerek kilóját tartalmazza. A párbeszédpanelnek ekkor a 27-3. ábrának kell megjelennie.
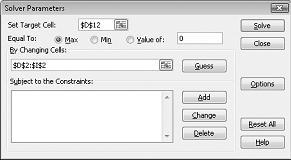
Most már készen állunk korlátozások hozzáadására a modellhez. Kattintson a Hozzáadás gombra. Megjelenik a Kényszer hozzáadása párbeszédpanel, amely a 27–4. ábrán látható.
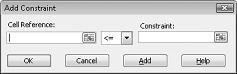
Az erőforrás-használati korlátozások hozzáadásához kattintson a Cellahivatkozás mezőre, majd válassza ki a D14:D15 tartományt. Válassza <= elemet a középső listából. Kattintson a Kényszer mezőre, majd jelölje ki az F14:F15 cellatartományt. A Kényszer hozzáadása párbeszédpanelnek ekkor a 27–5. ábrához hasonlóan kell kinéznie.
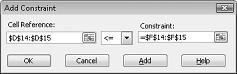
Most már gondoskodtunk arról, hogy amikor a Solver különböző értékeket próbál meg a változó cellákhoz, csak a D14<=F14 (a felhasznált munka kevesebb vagy egyenlő a rendelkezésre álló munkaerővel) és a D15<=F15 (a felhasznált nyersanyag kisebb vagy egyenlő a rendelkezésre álló nyersanyagéval) figyelembe lesz véve. Az igénykorlátozások megadásához kattintson a Hozzáadás gombra. Töltse ki a Kényszer hozzáadása párbeszédpanelt a 27–6. ábrán látható módon.
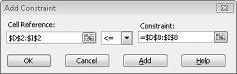
A kényszerek hozzáadása biztosítja, hogy amikor a Solver különböző kombinációkat próbál meg használni a változó cellaértékekhez, csak az alábbi paramétereknek megfelelő kombinációkat veszi figyelembe a rendszer:
-
D2<=D8 (az 1. gyógyszerből előállított mennyiség kisebb vagy egyenlő az 1. gyógyszer iránti keresletgel)
-
E2<=E8 (a 2. gyógyszer előállításának mennyisége kisebb vagy egyenlő a 2. gyógyszer iránti keresletgel)
-
F2<=F8 (a 3. gyógyszerből előállított mennyiség kisebb vagy egyenlő a 3. gyógyszer iránti keresletgel)
-
G2<=G8 (a 4. gyógyszerből előállított mennyiség kisebb vagy egyenlő a 4. gyógyszer iránti keresletgel)
-
H2<=H8 (az 5. kábítószerből előállított mennyiség kisebb vagy egyenlő az 5. kábítószer iránti keresletgel)
-
I2<=I8 (a 6. kábítószerből előállított mennyiség kisebb vagy egyenlő a 6. kábítószer iránti keresletgel)
Kattintson az OK gombra a Kényszer hozzáadása párbeszédpanelen. A Solver ablaknak a 27-7. ábrához hasonlóan kell kinéznie.
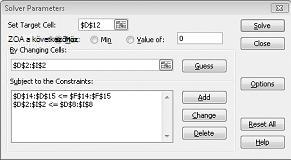
A Solver beállításai párbeszédpanelen azt a kényszert írjuk be, hogy a cellák módosításának nem szabad negatívnak lennie. Kattintson a Beállítások gombra a Solver paraméterei párbeszédpanelen. Jelölje be a Lineáris modell feltételezése jelölőnégyzetet és a Nem negatív feltételezés jelölőnégyzetet a következő oldalon, a 27-8. ábrán látható módon. Kattintson az OK gombra.

A Nem negatív feltételezése jelölőnégyzet bejelölésével biztosítható, hogy a Solver csak a változó cellák olyan kombinációit veszi figyelembe, amelyekben minden változó cella nem negatív értéket feltételez. Bejelöltük a Lineáris modell feltételezése jelölőnégyzetet, mert a termékkeverési probléma a Solver-probléma egy speciális típusa, az úgynevezett lineáris modell. A Solver-modell lényegében lineáris a következő feltételek mellett:
-
A célcella kiszámítása az űrlap kifejezéseinek összeadásával történik (változó cella)*(állandó).
-
Minden kényszer megfelel a "lineáris modellre vonatkozó követelménynek". Ez azt jelenti, hogy az egyes kényszerek kiértékelése úgy történik, hogy összeadja az űrlap kifejezéseit (változó cella)*(állandó), és összehasonlítja az összegeket egy állandóval.
Miért lineáris ez a Solver-probléma? A célcella (nyereség) kiszámítása a következőképpen történik:
(Gyógyszer 1 nyereség fontonként)*(Drog 1 font termelve) + (Gyógyszer 2 nyereség fontonként)*(Drog 2 font termelve) + ... (Gyógyszer 6 nyereség fontonként)*(Drog 6 font termelve)
Ez a számítás azt a mintát követi, amelyben a célcella értéke az űrlap kifejezéseinek összeadásával (változó cella)*(állandó) származtatható.
A munkaerő-korlátozást a (Felhasznált munka fontonként 1 gyógyszerből)*(A drog 1 fontja előállított) + (A felhasznált munka fontonként 2 gyógyszer)*(A kábítószer 2 kilója termelve)+ ... (Dolgozz velünked per font kábítószer 6)*(Kábítószer 6 font előállított) a munkaerő rendelkezésre áll.
Ezért a munkaerő-korlátozást úgy értékeli ki a rendszer, hogy összeadja az űrlap kifejezéseit (változó cella)*(állandó), és összehasonlítja az összegeket egy állandóval. A munkaerő- és a nyersanyagkényszer is megfelel a lineáris modellre vonatkozó követelménynek.
A keresleti korlátozások a következő formában alakulnak ki:
(1. gyógyszer előállítása)<=(1. gyógyszerkereslet) (Gyógyszer 2 előállított)<=(2. gyógyszer iránti kereslet) §(Drog 6 előállított)<=(Kábítószer 6 kereslet)
Minden keresleti kényszer megfelel a lineáris modellre vonatkozó követelménynek is, mivel mindegyik kiértékelése úgy történik, hogy összeadja az űrlap kifejezéseit (változó cella)*(állandó), és összehasonlítja az összegeket egy állandóval.
Miután kiderült, hogy a termékkeverés modellje lineáris modell, miért fontos nekünk?
-
Ha egy Solver-modell lineáris, és a Lineáris modell feltételezése lehetőséget választjuk, a Solver garantáltan megtalálja a Solver-modell optimális megoldását. Ha egy Solver-modell nem lineáris, előfordulhat, hogy a Solver megtalálja az optimális megoldást.
-
Ha egy Solver-modell lineáris, és a Lineáris modell feltételezése lehetőséget választjuk, a Solver egy nagyon hatékony algoritmust (a simplex metódust) használ a modell optimális megoldásának megkereséséhez. Ha egy Solver-modell lineáris, és nem a Lineáris modell feltételezése lehetőséget választjuk, a Solver nagyon nem hatékony algoritmust (GRG2 metódust) használ, és nehézséget okozhat a modell optimális megoldásának megkeresése.
Miután a Solver beállításai párbeszédpanelen az OK gombra kattintott, visszatérünk a Solver fő párbeszédpaneljére, amely a 27-7. ábrán látható. Amikor a Solvere kattintunk, a Solver kiszámít egy optimális megoldást (ha van ilyen) a termékkeverési modellünkhöz. Amint azt a 26. fejezetben már említettem, a termékkeverés modelljének optimális megoldása a változó sejtértékek (az egyes gyógyszerekből előállított fontok) készlete lenne, amely maximalizálja a nyereséget az összes megvalósítható megoldásnál. A megvalósítható megoldás az összes korlátozásnak megfelelő változó cellaértékek halmaza. A 27–9. ábrán látható változó cellaértékek megvalósítható megoldást jelentenek, mivel az összes termelési szint nem negatív, a termelési szintek nem haladják meg a keresletet, és az erőforrás-használat nem haladja meg a rendelkezésre álló erőforrásokat.
A következő oldalon a 27–10. ábrán látható változó cellaértékek az alábbi okokból nem megvalósítható megoldást jelentenek:
-
Többet gyártunk az 5-ös drogból, mint a kereslet.
-
A rendelkezésre állónál több munkaerőt használunk fel.
-
A rendelkezésre állónál több nyersanyagot használunk.
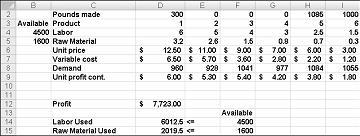
A Solver a Solver gombra kattintás után gyorsan megtalálja a 27–11. ábrán látható optimális megoldást. Az optimális megoldásértékek munkalapon való megőrzéséhez a Solver-megoldás megtartása lehetőséget kell választania.
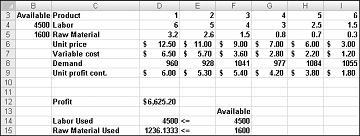
A kábítószer-társaság maximalizálhatja a havi nyereség szinten $ 6,625,20 előállításával 596,67 font Kábítószer 4, 1084 font Kábítószer 5, és egyik sem a többi gyógyszer! Nem tudjuk meghatározni, hogy a maximális nyereség 6625,20 $ más módon. Csak abban lehetünk biztosak, hogy a korlátozott erőforrásokkal és kereslettel nem lehet több, mint 6627,20 usd-t csinálni ebben a hónapban.
Tegyük fel, hogy az egyes termékek iránti keresletnek teljesülnie kell . (Lásd a nem megvalósítható megoldás munkalapot a fájl Prodmix.xlsx.) Ezután módosítani kell a keresleti korlátozásokat d2:I2<=D8:I8 értékről D2:I2>=D8:I8 értékre. Ehhez nyissa meg a Solvert, válassza a D2:I2<=D8:I8 kényszert, majd kattintson a Módosítás gombra. Megjelenik a 27–12. ábrán látható Megkötés módosítása párbeszédpanel.
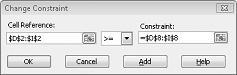
Válassza >=, majd kattintson az OK gombra. Gondoskodtunk arról, hogy a Solver csak azokat a cellaértékeket módosítsa, amelyek megfelelnek az összes követelménynek. Amikor a Solve (Megoldás) gombra kattint, a következő üzenet jelenik meg: "A Solver nem talált megvalósítható megoldást". Ez az üzenet nem azt jelenti, hogy hibát vétettünk a modellben, hanem azt, hogy korlátozott erőforrásainkkal nem tudjuk kielégíteni az összes termék iránti keresletet. A Solver egyszerűen azt mondja nekünk, hogy ha az egyes termékek iránti keresletet szeretnénk kielégíteni, több munkaerőt, több nyersanyagot vagy mindkettőt kell hozzáadnunk.
Nézzük meg, mi történik, ha korlátlan keresletet engedélyezünk minden termékre, és megengedjük, hogy negatív mennyiségeket állítsunk elő minden gyógyszerből. (Ez a Solver-probléma a fájlban található Set Values Do Not Converge (Nem konvergens értékek beállítása ) munkalapon jelenik meg Prodmix.xlsx.) Az optimális megoldás megtalálásához nyissa meg a Solvert, kattintson a Beállítások gombra, és törölje a Nem negatív feltételezés jelölőnégyzet jelölését. A Solver paraméterei párbeszédpanelen válassza ki a D2:I2<=D8:I8 igénykényszert, majd kattintson a Törlés gombra a kényszer eltávolításához. Amikor a Megoldás gombra kattint, a Solver a "Cellaértékek beállítása ne konvergens" üzenetet adja vissza. Ez az üzenet azt jelenti, hogy ha a célcella teljes méretűre van állítva (ahogy a példánkban is látható), akkor léteznek tetszőlegesen nagy célcellaértékeket tartalmazó megvalósítható megoldások. (Ha a célcella kis méretűre van állítva, a "Cellaértékek beállítása ne legyen konvergens" üzenet azt jelenti, hogy tetszőlegesen kis célcellaértékekkel rendelkező, megvalósítható megoldások állnak rendelkezésre.) A mi helyzetünkben a kábítószer negatív termelésének engedélyezésével tulajdonképpen olyan erőforrásokat "hozunk létre", amelyeket tetszőlegesen nagy mennyiségű más gyógyszer előállítására használhatunk fel. Tekintettel a korlátlan keresletre, ez lehetővé teszi számunkra, hogy korlátlan nyereséget. Valós helyzetben nem tudunk végtelen mennyiségű pénzt keresni. Röviden, ha a "Set Values Do Not Converge" (Az értékek beállítása nem konvergens) szöveget látja, a modell hibát jelez.
-
Tegyük fel, hogy a gyógyszercégünk akár 500 órányi munkát is vásárolhat óránként 1 dollárral többért, mint a jelenlegi munkaerőköltségek. Hogyan maximalizálhatjuk a profitot?
-
Egy forgácsgyárban négy technikus (A, B, C és D) három terméket gyárt (1., 2. és 3. termék). Ebben a hónapban a chipgyártó 80 egységet adhat el a Product 1-ből, 50 egységet a 2. termékből, és legfeljebb 50 egységet a 3. termékből. Az A technikus csak az 1. és a 3. terméket készítheti el. A B technikus csak az 1. és a 2. terméket készítheti el. A C technikus csak a 3. terméket készítheti el. A D technikus csak a 2. terméket készítheti el. Minden megtermelt egység esetében a termékek a következő nyereséggel járulnak hozzá: 1. termék, 6. usd; 2. termék, 7 usd; és Product 3, $ 10. Az egyes technikusok által a termék gyártásához szükséges idő (óra) a következő:
Termék
A technikus
B technikus
C technikus
Technikus D
1
2
2,5
Nem végezhető el
Nem végezhető el
2
Nem végezhető el
3
Nem végezhető el
3,5
3
3
Nem végezhető el
4
Nem végezhető el
-
Minden technikus akár 120 órát is dolgozhat havonta. Hogyan maximalizálhatja a chipgyártó a havi nyereségét? Tegyük fel, hogy tört számú egység állítható elő.
-
Egy számítógépgyártó üzem egereket, billentyűzeteket és videojáték-botkormányokat állít elő. Az egységenkénti nyereséget, az egységenkénti munkaerő-használatot, a havi keresletet és az egységenkénti gépi időhasználatot az alábbi táblázat tartalmazza:
Egerek
Billentyűzetek
Joystick
Nyereség/egység
8 USD
11 USD
9 USD
Munkaerő-használat/egység
.2 óra
0,3 óra
0,24 óra
Gépi idő/egység
0,04 óra
0,055 óra
0,04 óra
Havi igény
15 000
27,000
11,000
-
Havonta összesen 13 000 munkaóra és 3000 óra gépi idő áll rendelkezésre. Hogyan maximalizálhatja a gyártó a gyár havi nyereségét?
-
Oldja meg a gyógyszer példáját, feltéve, hogy minden gyógyszerhez legalább 200 egységnyi keresletet kell teljesíteni.
-
Jason gyémánt karkötőket, nyakláncokat és fülbevalókat készít. Havonta legfeljebb 160 órát szeretne dolgozni. 800 uncia gyémántja van. Az egyes termékek előállításához szükséges gyémántok nyereségét, munkaideét és unciait az alábbiakban tekintjük meg. Ha az egyes termékek iránti kereslet korlátlan, hogyan maximalizálhatja Jason a nyereségét?
Termék
Egység nyeresége
Munkaórák egységenként
Uncia gyémánt egységenként
Karkötő
30 000 Ft
.35
1.2
Nyaklánc
20 000 Ft
.15
.75
Fülbevaló
10 000 Ft
,05
.5










