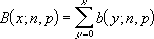A diszkrét binomiális eloszlás valószínűségértékét számítja ki. A BINOM.ELOSZLÁS függvényt olyan esetekben használja, amikor egy eset kimenetele kétesélyes: sikeres vagy sikertelen, az egyes esetek egymástól teljes mértékben függetlenek, és amikor az eredmény valószínűsége az egész kísérlet alatt állandó. A BINOM.ELOSZLÁS függvénnyel például kiszámíthatja, hogy mi az esélye annak, hogy a következő három világra jövő gyermek közül kettő fiú lesz.
Fontos: Ezt a függvényt pontosabban működő és a felhasználást jobban tükröző nevű új függvények váltották fel. Bár a függvény az Excel korábbi verzióival való kompatibilitás végett továbbra is elérhető, előfordulhat, hogy az Excel jövőbeli verziói már nem tartalmazzák, ezért a továbbiakban célszerű az új függvényeket használni.
Az új függvénnyel kapcsolatos további információkért lásd a BINOM.ELOSZL függvény című témakört.
Szintaxis
BINOM.ELOSZLÁS(sikeresek;kísérletek;siker_valószínűsége;eloszlásfv)
A BINOM.ELOSZLÁS függvény szintaxisa az alábbi argumentumokat foglalja magában:
-
Sikeresek: Megadása kötelező. A sikeres kísérletek száma.
-
Kísérletek: Megadása kötelező. A független kísérletek száma.
-
Siker_valószínűsége: Megadása kötelező. A siker valószínűsége az egyes kísérletek esetén.
-
Eloszlásfv: Megadása kötelező. Logikai érték, amely a függvény fajtáját határozza meg. Ha az eloszlás értéke IGAZ, akkor a BINOM.ELOSZLÁS függvény az eloszlásfüggvény értékét számítja ki, amely annak a valószínűsége, hogy legfeljebb number_s sikeresek; ha HAMIS, akkor a valószínűségi tömegfüggvényt adja vissza, amely annak a valószínűsége, hogy number_s sikeresek.
Megjegyzések
-
A sikeresek és a kísérletek számát a függvény egésszé csonkolja.
-
Ha number_s, kísérletek vagy probability_s nem számérték, akkor a BINOM.ELOSZLÁS eredménye a #VALUE! hibaértéket adja vissza.
-
Ha a sikeres_kimenetelek < 0 vagy a sikeresek > kísérletek, a BINOM.ELOSZLÁS függvény a #SZÁM! hibaértéket adja eredményül.
-
Ha a siker_valószínűsége < 0 vagy a siker_valószínűsége > 1, akkor a BINOM.ELOSZLÁS függvény a #SZÁM! hibaértéket adja vissza.
-
Ha x = sikeresek, n = kísérletek és p = siker_valószínűsége, akkor a binomiális sűrűségfüggvény:
ahol:
a KOMBINÁCIÓK(n;x).
-
Ha x = sikeresek, n = kísérletek és p = siker_valószínűsége, akkor a binomiális eloszlásfüggvény:
Példa
Másolja a mintaadatokat az alábbi táblázatból, és illessze be őket egy új Excel-munkalap A1 cellájába. Ha azt szeretné, hogy a képletek megjelenítsék az eredményt, jelölje ki őket, és nyomja le az F2, majd az Enter billentyűt. Szükség esetén módosíthatja az oszlopok szélességét, hogy az összes adat látható legyen.
|
Adatok |
Leírás |
|
|
6 |
A sikeres kísérletek száma |
|
|
10 |
A független kísérletek száma |
|
|
0,5 |
A siker valószínűsége az egyes kísérletek esetén |
|
|
Képlet |
Leírás |
Eredmény |
|
=BINOM.ELOSZLÁS(A2;A3;A4;HAMIS) |
10 kísérletből pontosan 6 sikerességének a valószínűsége |
0,2050781 |