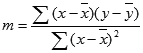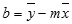LIN.ILL függvény

Leírás

A LIN.ILL függvény a legkisebb négyzetek módszerével kiszámolja a megadott adatokhoz legjobban illeszkedő egyenes egyenletét, és eredményként az egyenest leíró tömböt adja vissza. A LIN.ILL más függvényekkel együtt való használatával kiszámíthatja lineáris ismeretlen paraméterekkel rendelkező, más típusú (például logaritmikus, polinomiális, exponenciális és hatványsor-) modellek statisztikáit is. Mivel ez a függvény tömböt ad eredményül, tömbképletként kell bevinni. A cikkben a példákat útmutató követi.

Az egyenes egyenlete a következő:

y = mx + b

– vagy –

y = m1x1 + m2x2 + ... + b

ha több x értéktartomány is meg van adva, ahol az y értékek a független x értékek függvényei. Az m értékek az egyes x értékek együtthatói, míg a b állandó érték. Az y, az x és az m érték vektor is lehet. A LIN.ILL függvény az {mn;mn-1;...;m1;b} tömböt adja eredményül. A LIN.ILL függvény egyéb regressziós statisztikai adatokat is vissza tud adni.

Szintaxis

LIN.ILL(ismert_y; [ismert_x]; [konstans]; [stat])

A LIN.ILL függvény szintaxisa az alábbi argumentumokat foglalja magában:

Szintaxis

• ismert_y:    Megadása kötelező. Az y = mx + b összefüggésből már ismert y értékek.

  • Ha az ismert_y értékek tartománya egyetlen oszlop, akkor az ismert_x értékek minden egyes oszlopát különböző változóként értelmezi a függvény.

  • Ha az ismert_y értékek tartománya egyetlen sor, akkor az ismert_x értékek minden egyes sorát különböző változóként értelmezi a függvény.

• ismert_x:    Megadása nem kötelező. Az y = mx + b összefüggésből már ismert x értékek.

  • Az ismert_x értékek tartománya egy vagy több különböző változó értékeit tartalmazhatja. Ha csak egy változót használ, akkor az ismert_y és az ismert_x tetszőleges alakú, egyenlő dimenziójú tartomány lehet. Ha egynél több változót használ, akkor az ismert_y tartománynak vektornak kell lennie (amely egyetlen sor magasságú vagy egyetlen oszlop szélességű tartomány).

  • Ha az ismert_x argumentumot nem adja meg, akkor a függvény az {1. 2. 3. ...} tömböt használja, amely az ismert_x tömbbel azonos méretű.

• konstans:    Megadása nem kötelező. Logikai érték, amely azt határozza meg, hogy a b értéke mindenképpen 0 legyen-e.

  • Ha a konstans értéke IGAZ vagy hiányzik, akkor a függvény a b értéket korlátozás nélkül számolja ki.

  • Ha a konstans értéke HAMIS, akkor a b értéke 0 lesz, az m értékeket pedig az y = mx egyenlet alapján számolja ki a függvény.

• stat:    Megadása nem kötelező. Logikai érték, amely azt határozza meg, hogy a függvény kiegészítő regressziós statisztikai adatokat is számoljon-e.

  • Ha a statisztikák ÉRTÉKE IGAZ, akkor a LIN.T a további regressziós statisztikákat adja vissza; Ennek eredményeként a visszaadott tömb { mn,mn-1,...,m1,b; sen,sen-1,...,se1,seb; r^2,sey; F,df; ssreg,ssresid}.

  • Ha a stat argumentum értéke HAMIS vagy hiányzik, akkor a LIN.ILL csak az m együtthatókat és a b állandót adja eredményül.

    A kiegészítő regressziós adatok a következők:

A következő táblázat azt mutatja be, hogy a függvény milyen sorrendben adja meg a kiegészítő regressziós statisztikai adatokat.

Megjegyzések

• Minden egyenes egyenlete megadható meredekségének és az y tengellyel való metszéspontjának segítségével:

  Meredekség (m):
  A gyakran m-ként írt egyenes meredekségének megkereséséhez vegyen két pontot a vonalon (x1,y1) és (x2,y2); a meredekség egyenlő (y2 - y1)/(x2 - x1).

  Y-metszéspont (b):
  Egy vonal y-metszete, amelyet gyakran b-ként írnak, az y értéke azon a ponton, ahol a vonal átlépi az y tengelyt.

  Az egyenes egyenlete y = mx + b. Ha ismeri az m és a b értéket, akkor az egyenes tetszőleges pontjának koordinátái kiszámíthatók az ismert x vagy y érték behelyettesítésével. Emellett használhatja a TREND függvényt is.

• Ha csak egyetlen független x-változóval dolgozik, akkor a meredekséget és az egyenes y tengellyel való metszéspontját a következő függvények felhasználásával kaphatja meg közvetlenül:

  Lejtő:
  =INDEX(LIN.ILL(known_y;known_x);1)

  Y-metszéspont:
  =INDEX(LIN.ILL(known_y;known_x);2)

• A LIN.ILL függvénnyel kiszámolt egyenes pontossága függ a felhasznált adatok szórásának nagyságától. A függő és a független változók kapcsolata minél inkább közelít a lineárishoz, annál pontosabb a LIN.ILL modell. A LIN.ILL a legkisebb négyzetek módszerét használja az adatokhoz legjobban illeszkedő egyenes meghatározására. Ha csak egyetlen független x változóval dolgozik, akkor az m és a b érték kiszámítása a következő egyenletek segítségével történik:

  

  

  ahol x és y az adatok középértékei, tehát x = ÁTLAG(ismert_ x) és y = ÁTLAG(ismert_y).

• A LIN.ILL és a LOGEST vonal- és görbeillesztési függvények az adatoknak leginkább megfelelő egyenes vagy exponenciális görbét számíthatják ki. Azonban el kell döntenie, hogy a két eredmény közül melyik felel meg a legjobban az adatainak. Kiszámíthatja a TREND(known_y,known_x) értékét egy egyeneshez, vagy a GROWTH(known_y, known_x) képletet exponenciális görbére. Ezek a függvények a new_x argumentuma nélkül az adott vonal vagy görbe mentén előrejelzett y értékek tömbjét adnak vissza a tényleges adatpontoknál. Ezután összehasonlíthatja az előrejelzett értékeket a tényleges értékekkel. A vizualizációk összehasonlításához érdemes lehet mindkettőt ábrázolni.

• A regresszióanalízis során a Microsoft Excel kiszámítja az egyes becsült és tényleges y értékek eltéréseinek négyzetét. Ezeknek az eltérésnégyzeteknek az összege a maradék négyzetösszeg, ssresid. Az Excel ezután kiszámítja a négyzetek teljes összegét, az sstotal értéket. Ha a konstans argumentum értéke IGAZ vagy nincs megadva, akkor a teljes négyzetösszeg egyenlő az y értékek átlagának és a tényleges y értékek eltéréseinek négyzetösszegével. Ha a konstans argumentum értéke HAMIS, akkor a teljes négyzetösszeg a tényleges y értékek négyzetösszege (az y értékek átlagának az egyes y értékekből történő kivonása nélkül). A regressziós négyzetösszeg – ssreg – a következőképpen számítható ki: ssreg = sstotal - ssresid. Minél kisebb a négyzetek reziduálisösszege a négyzetek teljes összegével összehasonlítva, annál nagyobb az r² meghatározási együttható értéke, amely azt jelzi, hogy a regresszióelemzésből származó egyenlet mennyire jól magyarázza a változók közötti kapcsolatot. Az r² értéke ssreg/sstotal.

• Bizonyos esetekben előfordulhat, hogy egy vagy több X oszlop (feltételezve, hogy az Y és az X oszlopban található) nem feltétlenül rendelkezik további prediktív értékkel a többi X oszlop jelenlétében. Más szóval egy vagy több X oszlop megszüntetése olyan előrejelzett Y értékekhez vezethet, amelyek egyformán pontosak. Ebben az esetben ezeket a redundáns X oszlopokat ki kell hagyni a regressziós modellből. Ezt a jelenséget "kollinearitásnak" nevezik, mert minden redundáns X oszlop a nem redundáns X oszlopok többszöröseinek összegeként fejezhető ki. A LIN.VONAL függvény ellenőrzi a kollinearitást, és eltávolítja a redundáns X oszlopokat a regressziós modellből, amikor azonosítja őket. Az eltávolított X oszlopok a LINEST kimenetben 0 együtthatóként ismerhetők fel a 0 se értékek mellett. Ha egy vagy több oszlopot redundánsként távolít el, a df az érintett, mert a df a prediktív célokra ténylegesen használt X oszlopok számától függ. A df számításával kapcsolatos részletekért lásd a 4. példát. Ha a redundáns X oszlopok eltávolítása miatt a df módosul, a sey és az F értékei is érintettek lesznek. A kollinearitásnak a gyakorlatban viszonylag ritkanak kell lennie. Az egyik eset azonban, amikor nagyobb a valószínűsége annak, hogy egyes X oszlopok csak 0 és 1 értéket tartalmaznak annak jelzéseként, hogy egy kísérlet tárgya egy adott csoport tagja-e vagy sem. Ha a const = IGAZ vagy nincs megadva, a LIN.ELT függvény hatékonyan beszúr egy további X oszlopot mind az 1 értékből az metszéspont modellezéséhez. Ha egy oszlopban minden tárgyhoz 1 tartozik, ha férfi, vagy 0, ha nem, és van egy oszlopa is, amelyben minden tárgyhoz tartozik egy 1, ha nő, vagy 0, ha nem, ez utóbbi oszlop redundáns, mert a benne lévő bejegyzések a "férfi mutató" oszlop bejegyzésének kivonásából nyerhetők ki a LIN.T függvény által hozzáadott 1 érték további oszlopában lévő bejegyzésből.

• Ha kollinearitás miatt nem kellett eltávolítani egyetlen X oszlopot sem, akkor a df értékét a következőképpen lehet kiszámolni: ha k darab ismert_x oszlop van és a konstans = IGAZ vagy hiányzik: df = n – k – 1. Ha a konstans = HAMIS: df = n - k. A kollinearitás miatt eltávolított minden egyes oszlop mindkét esetben 1-gyel növeli a df értékét.

• Ha argumentumként tömböt ad meg (ilyen lehet például az ismert_x értékek tömbje), akkor az egy sorba tartozó értékeket ponttal, az egyes sorokat pontosvesszővel válassza el egymástól. A listaelválasztó karakterek a területi beállításoktól függenek.

• Ne feledje, hogy a regressziós egyenlet által előre jelzett y értékek nem alkalmazhatók, ha kívül esnek az egyenlet meghatározására megadott y értékek tartományán.

• A LIN.ILL függvény mögöttes algoritmusa eltér a MEREDEKSÉG és a METSZ függvényétől. Az algoritmusok különbözősége eltérő eredményekhez vezethet, ha az adatok határozatlanok és kollineárisak. Ha például az ismert_y adatpontok 0 értékűek, illetve az ismert_x adatpontjai 1 értékűek:

  • A LIN.ILL függvény értéke 0. A LIN.ILL algoritmus úgy van kialakítva, hogy kollineáris adatok esetén ésszerű eredményeket adjon, és ebben az esetben legalább egy válasz létezik.

  • A MEREDEKSÉG és a METSZ függvény értéke #ZÉRÓOSZTÓ! hiba. A MEREDEKSÉG és a METSZ algoritmus úgy van kialakítva, hogy kizárólag egy választ keressen, és ebben az esetben egynél több válasz lehetséges.

• Azonfelül, hogy a LOG.ILL függvény segítségével statisztikai számításokat végezhet más típusú regressziók esetében, a LIN.ILL segítségével számításokat végezhet sok más regressziótípus esetében, ha az x és y változók függvényét x és y sorozatok formájában megadja a LIN.ILL függvénynek. Például a következő képlet:

  =LIN.ILL(yértékek; xértékek^OSZLOP($A:$C))

  akkor használható, ha az y és x értékek egy-egy oszlopban találhatók, és a következő egyenlet köbös (harmadrendű polinomiális) közelítését szeretné kiszámítani:

  y = m1*x + m2*x^2 + m3*x^3 + b

  E képlet módosított változataival kiszámíthat más típusú regressziót is, egyes esetekben azonban módosítani kell a kimeneti értékeket és más statisztikákat.

• A LIN.ILL függvény által visszaadott F-próba érték eltér az F.PRÓBA függvény által adott F-próba értékétől. A LIN.ILL függvény a statisztikai F értékét adja meg, míg az F.PRÓBA függvény a valószínűséget.

Példák