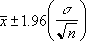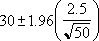Egy normális eloszlású sokaság középértékének megbízhatósági intervallumát adja eredményül. A megbízhatósági intervallum a minta középértékének mindkét oldalán található tartomány. Ha például e-mailben rendel egy terméket, egy bizonyos megbízhatósági szinttel meghatározhatja, hogy a legkorábbi és legújabb termék érkezik-e.
Szintaxis
MEGBÍZHATÓSÁG(alfa;standard_dev;méret)
Alfa: A a megbízhatósági szint kiszámításához használt pontossági szint. A megbízhatósági szint egyenlő 100*(1-alfa), vagyis a 0,05 alfaérték 95%-os megbízhatósági szintet takar.
Szórás: az adattartomány statisztikai szórása, és ismertnek kell lennie.
Méret: A a minta mérete.
Megjegyzések:
-
Ha bármelyik argumentum nem számérték, akkor a MEGBÍZHATÓSÁG függvény a #VALUE! hibaértéket adja eredményül.
-
Ha az alfa ≤ 0 vagy alfa ≥ 1, akkor a MEGBÍZHATÓSÁG függvény a #NUM! hibaértéket adja eredményül.
-
Ha standard_dev ≤ 0, akkor a MEGBÍZHATÓSÁG függvény a #NUM adja vissza. hibaértéket adja eredményül.
-
Amennyiben a méret nem egész szám, egésszé lesz csonkítva.
-
Ha a méret < 1, akkor a MEGBÍZHATÓSÁG függvény a #NUM! hibaértéket adja eredményül.
-
Ha feltételezi, hogy az alfa értéke 0,05, akkor a normális (eloszlás)görbe alatti területtel (1- alfa) kell számolnia (95%). Ez az érték ± 1,96. A megbízhatósági intervallum ebből adódóan:
Példa
Tegyük fel, hogy az 50 ingázót tartalmazó mintánkban a munkába menet átlagos hossza 30 perc, a statisztikai szórás pedig 2,5. 95%-ig biztosak lehetünk abban, hogy a populáció középértékének intervalluma a következő:
|
Alfa: |
Szórás |
Méret: |
Képlet |
Eredmény |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=MEGBÍZHATÓSÁG([Alfa];[Szórás];[Méret]) |
Statisztikai sokaság megbízhatósági intervalluma. Más szóval a munkához való utazás átlagos hossza 30 ± 0,692951 perc, azaz 29,3 és 30,7 perc között van. (0.692951) |