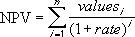NMÉ függvény

Szintaxis

NMÉ(ráta;érték1;érték2;...)

Ráta:     az egy időszak alatt érvényes leszámítolási ráta.

Value1, value2,...     A kifizetéseket és a bevételeket 1–29 argumentum jelöli. Value1, value2,... az időtartománynak egyenlőnek kell lennie, és minden időszak végén meg kell történnie. NMÉ az érték1 és az érték2 sorrendjét használja,... a pénzáramlások sorrendjének értelmezéséhez. Ügyeljen arra, hogy a megfelelő sorrendben adja meg a fizetési és a bevételi értékeket. A számokat, üres, logikai értékeket vagy számok szöveges ábrázolását tartalmazó argumentumokat a függvény megszámolja; a függvény figyelmen kívül hagyja a hibaértékeket vagy a számmá nem fordítható szöveget tartalmazó argumentumokat.

Megjegyzések:

• Az NMÉ befektetése az érték1 időpontja előtt egy időszakkal kezdődik és az utolsó pénzáramlás időpontjában fejeződik be. A nettó jelenérték kiszámítása jövőbeni pénzáramlásokon alapszik. Ha az első pénzáramlás az első periódus elején esedékes, ezt az ellenértéket nem szabad a változók között szerepeltetni, hanem a számítás után hozzá kell adni az NMÉ eredményéhez. Az alábbi példák is ezt szemléltetik.

• Ha n az értékek listájában szereplő pénzáramlások száma, akkor az NMÉ az alábbi képlet alapján számolja ki a nettó jelenértéket:

  

• Az NMÉ hasonló az MÉ függvényhez. A legfontosabb különbség köztük az, hogy az MÉ függvényben a pénzáramlások az időszakok elején és végén egyaránt történhetnek. Az NMÉ függvénytől eltérően az MÉ változóinak időben állandóaknak kell lenniük minden időszakban. Az annuitásokról és pénzügyi függvényekről további információ az MÉ függvény leírásánál található.

1. példa

Az alábbi példában:

• A ráta az éves diszkontráta.

• Az Érték1 a befektetés kezdeti költsége egy év múlva.

• A Value2 az első évből származó eredmény.

• A Value3 a második évből származó eredmény.

• A Value4 a harmadik év eredménye.

A példában a kezdeti 10 000 USD költséget adja meg az értékek egyikeként, mivel a kifizetés az első időszak végén történik.

2. példa

Az alábbi példában:

• A ráta az éves diszkontráta. Ez lehet az inflációs ráta vagy más lehetséges befektetés kamatlába.

• Az Érték1 a befektetés kezdeti költsége egy év múlva.

• A Value2 az első évből származó eredmény.

• A Value3 a második évből származó eredmény.

• A Value4 a harmadik év eredménye.

• Az 5. érték a negyedik évből származó eredmény.

• A Value6 az ötödik év eredménye.

A példában nem szerepel a kezdeti 40 000 ft-os költség az értékek egyikeként, mert a kifizetés az első időszak elején történik.