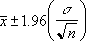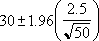Restituisce l'intervallo di confidenza per una media della popolazione con una distribuzione normale. L'intervallo di confidenza è un intervallo su entrambi i lati di una media campione. Ad esempio, se ordini un prodotto tramite posta elettronica, puoi determinare, con un particolare livello di probabilità, l'arrivo del prodotto il più presto e l'ultima volta.
Sintassi
CONFIDENZA(alfa; standard_dev; dimensione)
Alfa è il livello di significatività utilizzato per calcolare il livello di probabilità. Il livello di probabilità è uguale a 100*(1 - alfa)% o, in altre parole, un valore alfa di 0,05 indica un livello di probabilità del 95%.
Dev_standard è la deviazione standard della popolazione per l'intervallo di dati e si presuppone che sia nota.
Dimensioni è la dimensione del campione.
Osservazioni
-
Se un qualsiasi argomento non è numerico, CONFIDENZA restituirà il #VALUE! .
-
Se alfa ≤ 0 o alfa ≥ 1, CONFIDENZA restituirà il #NUM! .
-
Se standard_dev ≤ 0, CONFIDENZA restituirà il #NUM! .
-
Se dimens non è un numero intero, la parte decimale verrà troncata.
-
Se dimensione < 1, CONFIDENZA restituirà il #NUM! .
-
Se si suppone che alfa sia uguale a 0,05, sarà necessario calcolare l'area sottostante la curva normale standard che è uguale a (1 - alfa) o al 95%. Questo valore è ± 1,96. L'intervallo di confidenza sarà quindi:
Esempio
Si supponga di osservare che, nel campione di 50 pendolari, la durata media del viaggio al lavoro è di 30 minuti con una deviazione standard della popolazione di 2,5. Possiamo essere sicuri del 95% che la media della popolazione sia nell'intervallo:
|
Alfa |
StdDev |
Dimensioni |
Formula |
Descrizione (risultato) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENZA([Alfa],[DevSt],[Dimensioni]) |
Intervallo di confidenza per la media della popolazione. In altre parole, la lunghezza media del viaggio verso il lavoro è uguale a 30 ± 0,692951 minuti o da 29,3 a 30,7 minuti. (0.692951) |