Importante: Il supporto per Office 2016 e Office 2019 è terminato il 14 ottobre 2025. Esegui l'aggiornamento a Microsoft 365 per lavorare ovunque da qualsiasi dispositivo e continuare a ricevere il supporto. Ottenere Microsoft 365
Questo articolo descrive l'uso del Risolutore, un componente aggiuntivo di Microsoft Excel che è possibile usare per l'analisi di simulazione, per determinare una combinazione ottimale di prodotti.
Come è possibile determinare la combinazione mensile di prodotti che ottimizza la redditività?
Spesso le aziende devono determinare la quantità di ciascun prodotto da produrre mensilmente. Nella sua forma più semplice, il problema della combinazione di prodotti prevede come determinare l'importo di ogni prodotto che dovrebbe essere prodotto durante un mese per massimizzare i profitti. La combinazione di prodotti deve in genere rispettare i seguenti vincoli:
-
La combinazione di prodotti non può usare più risorse di quelle disponibili.
-
C'è una domanda limitata per ogni prodotto. Non possiamo produrre più di un prodotto durante un mese rispetto alla domanda detta, perché la produzione in eccesso è sprecata (ad esempio, un farmaco deperibile).
Risolviamo ora l'esempio seguente del problema relativo alla combinazione di prodotti. La soluzione a questo problema è disponibile nella Prodmix.xlsx di file, illustrata nella figura 27-1.
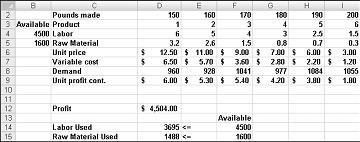
Supponiamo di lavorare per un'azienda produttrice di farmaci che produce sei prodotti diversi nel loro stabilimento. La produzione di ciascun prodotto richiede manodopera e materie prime. La riga 4 della figura 27-1 mostra le ore di lavoro necessarie per produrre un chilo di ogni prodotto, mentre la riga 5 mostra i libbre di materia prima necessaria per produrre un chilo di ogni prodotto. Ad esempio, la produzione di un chilo di prodotto 1 richiede sei ore di lavoro e 3,2 libbre di materia prima. Per ogni farmaco, il prezzo per sterlina è dato nella riga 6, il costo unitario per sterlina è dato nella riga 7, e il contributo di profitto per sterlina è dato nella riga 9. Ad esempio, il prodotto 2 viene venduto per $ 11,00 per sterlina, incorre in un costo unitario di $ 5,70 per sterlina e contribuisce a un profitto di $ 5,30 per sterlina. La domanda del mese per ogni farmaco è data nella riga 8. Ad esempio, la domanda per il prodotto 3 è 1041 libbre. Questo mese sono disponibili 4500 ore di lavoro e 1600 libbre di materia prima. Come può questa azienda massimizzare il suo profitto mensile?
Se non si conoscesse nulla del Risolutore di Excel, si potrebbe attaccare questo problema creando un foglio di lavoro per tenere traccia del profitto e dell'uso delle risorse associato al mix di prodotti. Poi useremmo la prova e l'errore per variare la combinazione di prodotti per ottimizzare il profitto senza usare più lavoro o materia prima di quanto è disponibile, e senza produrre alcun farmaco in eccesso della domanda. Il Risolutore viene usato in questo processo solo nella fase di prova e di errore. Essenzialmente, il Risolutore è un motore di ottimizzazione che esegue perfettamente la ricerca di tentativi ed errori.
Una chiave per risolvere il problema della combinazione di prodotti consiste nel calcolare in modo efficiente l'utilizzo delle risorse e il profitto associato a un determinato mix di prodotti. Uno strumento importante che possiamo usare per eseguire questo calcolo è la funzione MATR.SOMMA.PRODOTTO. La funzione MATR.SOMMA.PRODOTTO moltiplica i valori corrispondenti negli intervalli di celle e restituisce la somma di tali valori. Ogni intervallo di celle usato in una MATR.SOMMA.PRODOTTO valutazione deve avere le stesse dimensioni, il che implica che è possibile usare MATR.SOMMA.PRODOTTO con due righe o due colonne, ma non con una colonna e una riga.
Come esempio di come possiamo usare la funzione MATR.SOMMA.PRODOTTO nell'esempio della nostra combinazione di prodotti, proviamo a calcolare l'utilizzo delle risorse. Il nostro utilizzo del lavoro viene calcolato
(Lavoro usato per chilo di droga 1)*(Farmaco 1 libbra prodotta)+ (Lavoro usato per chilo di droga 2)*(Droga 2 libbre prodotte) + ... (Lavoro usato per chilo di droga 6)*(Farmaco 6 libbre prodotte)
È possibile calcolare l'utilizzo del lavoro in modo più noioso come D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Analogamente, l'utilizzo delle materie prime potrebbe essere calcolato come D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Tuttavia, l'immissione di queste formule in un foglio di lavoro per sei prodotti richiede molto tempo. Immaginate quanto tempo ci vorrebbe se lavoraste con un'azienda che produce, ad esempio, 50 prodotti presso il loro stabilimento. Un modo molto più semplice per calcolare il consumo di manodopera e materie prime consiste nel copiare da D14 a D15 la formula MATR.SOMMA.PRODOTTO($D$2:$I$2,D4:I4). Questa formula calcola D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (che è il nostro utilizzo del lavoro), ma è molto più facile da immettere! Si noti che uso il segno $ con l'intervallo D2:I2 in modo che quando copo la formula acquisisco ancora il mix di prodotti dalla riga 2. La formula nella cella D15 calcola l'utilizzo delle materie prime.
In modo analogo, il nostro profitto è determinato da
(Farmaco 1 profitto per sterlina)*(Droga 1 libbra prodotta) + (Farmaco 2 profitto per sterlina)*(Droga 2 libbre prodotte) + ... (Farmaco 6 profitto per sterlina)*(Farmaco 6 libbre prodotte)
Il profitto viene calcolato facilmente nella cella D12 con la formula MATR.SOMMA.PRODOTTO(D9:I9,$D$2:$I$2)).
Ora è possibile identificare i tre componenti del modello Risolutore della nostra combinazione di prodotti.
-
Cella di destinazione. Il nostro obiettivo è quello di massimizzare il profitto (calcolato nella cella D12).
-
Celle variabili. Il numero di libbre prodotte di ogni prodotto (indicato nell'intervallo di celle D2:I2)
-
Vincoli. I vincoli sono i seguenti:
-
Non utilizzare più lavoro o materia prima di quanto sia disponibile. Ovvero, i valori nelle celle D14:D15 (risorse usate) devono essere minori o uguali ai valori nelle celle F14:F15 (le risorse disponibili).
-
Non produrre più di un farmaco di quanto sia richiesto. Ovvero, i valori nelle celle D2:I2 (libbre prodotte da ogni farmaco) devono essere inferiori o uguali alla domanda di ogni farmaco (elencati nelle celle D8:I8).
-
Non possiamo produrre una quantità negativa di qualsiasi farmaco.
-
Ti mostrerò come immettere la cella di destinazione, cambiare le celle e i vincoli in Risolutore. Quindi tutto quello che dovete fare è fare clic sul pulsante Risolvi per trovare una combinazione di prodotti che ottimizza il profitto!
Per iniziare, fare clic sulla scheda Dati e quindi nel gruppo Analisi fare clic su Risolutore.
Nota: Come spiegato nel Capitolo 26, "Introduzione all'ottimizzazione con il Risolutore di Excel", il Risolutore viene installato facendo clic sul pulsante Microsoft Office, quindi su Opzioni di Excel, seguito da Componenti aggiuntivi. Nell'elenco Gestisci fare clic su Componenti aggiuntivi di Excel, selezionare la casella Componente aggiuntivo Risolutore e quindi fare clic su OK.
Verrà visualizzata la finestra di dialogo Parametri Risolutore, come illustrato nella figura 27-2.
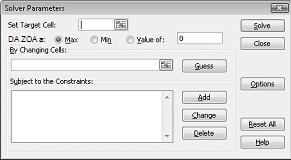
Fare clic sulla casella Imposta cella di destinazione e quindi selezionare la cella di profitto (cella D12). Fare clic sulla casella Cambiando le celle e quindi posizionare il puntatore del mouse sull'intervallo D2:I2, che contiene i libbre prodotti da ogni farmaco. La finestra di dialogo dovrebbe ora apparire nella figura 27-3.
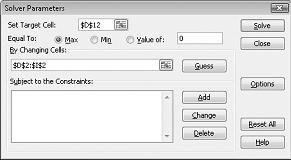
Ora siamo pronti per aggiungere vincoli al modello. Fare clic sul pulsante Aggiungi. Verrà visualizzata la finestra di dialogo Aggiungi vincolo, illustrata nella figura 27-4.
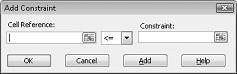
Per aggiungere i vincoli di utilizzo delle risorse, fare clic sulla casella Riferimento di cella e quindi selezionare l'intervallo D14:D15. Selezionare <= nell'elenco centrale. Fare clic sulla casella Vincolo e quindi selezionare l'intervallo di celle F14:F15. La finestra di dialogo Aggiungi vincolo dovrebbe ora essere simile alla figura 27-5.
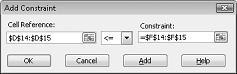
Ora abbiamo fatto in modo che quando il Risolutore prova valori diversi per le celle variabili, verranno prese in considerazione solo le combinazioni che soddisfano sia D14<=F14 (il lavoro utilizzato è minore o uguale al lavoro disponibile) che D15<=F15 (la materia prima utilizzata è minore o uguale alla materia prima disponibile). Fare clic su Aggiungi per immettere i vincoli di domanda. Compilare la finestra di dialogo Aggiungi vincolo come illustrato nella figura 27-6.
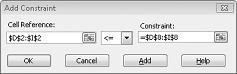
L'aggiunta di questi vincoli assicura che, quando il Risolutore prova diverse combinazioni per i valori variabili delle celle, verranno prese in considerazione solo le combinazioni che soddisfano i seguenti parametri:
-
D2<=D8 (la quantità prodotta di Farmaco 1 è inferiore o uguale alla domanda di farmaco 1)
-
E2<=E8 (la quantità di droga prodotta 2 è inferiore o uguale alla domanda di farmaco 2)
-
F2<=F8 (la quantità prodotta di Farmaco 3 è minore o uguale alla domanda di Farmaco 3)
-
G2<=G8 (la quantità prodotta di Farmaco 4 fatta è inferiore o uguale alla domanda di Farmaco 4)
-
H2<=H8 (la quantità prodotta di Farmaco 5 fatta è inferiore o uguale alla domanda di farmaco 5)
-
I2<=I8 (la quantità prodotta di Farmaco 6 è minore o uguale alla domanda di Farmaco 6)
Fare clic su OK nella finestra di dialogo Aggiungi vincolo. La finestra del Risolutore sarà simile alla Figura 27-7.
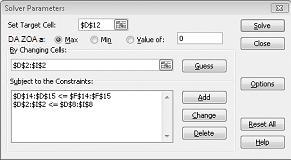
Immettere il vincolo che indica che le celle modificate devono essere non negative nella finestra di dialogo Opzioni Risolutore. Fare clic sul pulsante Opzioni nella finestra di dialogo Parametri Risolutore. Selezionare le caselle Presuppone modello lineare e Assume non negativo, come illustrato nella figura 27-8 della pagina successiva. Fare clic su OK.
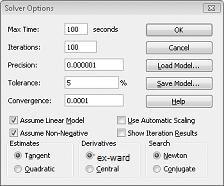
Selezionando la casella Presuppone che il Risolutore consideri solo le combinazioni di celle variabili in cui ogni cella modificante presuppone un valore non negativo. Abbiamo controllato la casella Presuppone modello lineare perché il problema della combinazione di prodotti è un tipo speciale di problema del Risolutore chiamato modello lineare. Essenzialmente, un modello del Risolutore è lineare nelle condizioni seguenti:
-
La cella di destinazione viene calcolata sommando i termini della maschera (cella modificata)*(costante).
-
Ogni vincolo soddisfa il "requisito del modello lineare". Questo significa che ogni vincolo viene valutato sommando i termini della maschera (cella modificante)*(costante) e confrontando le somme con una costante.
Perché questo problema del Risolutore è lineare? La cella di destinazione (profitto) viene calcolata come
(Farmaco 1 profitto per sterlina)*(Droga 1 libbra prodotta) + (Farmaco 2 profitto per sterlina)*(Droga 2 libbre prodotte) + ... (Farmaco 6 profitto per sterlina)*(Farmaco 6 libbre prodotte)
Questo calcolo segue uno schema in cui il valore della cella di destinazione viene derivato sommando i termini della forma (cella variabile)*(costante).
Il nostro vincolo di lavoro viene valutato confrontando il valore derivato da (Lavoro usato per libbra di Farmaco 1)*(Farmaco 1 libbra prodotta) + (Lavoro usato per chilo di Droga 2)*(Farmaco 2 libbre prodotte)+ ... (Lavoracied per chilo di Droga 6)*(Farmaco 6 libbre prodotte) al lavoro disponibile.
Di conseguenza, il vincolo di lavoro viene valutato sommando i termini della maschera (cella modificante)*(costante) e confrontando le somme con una costante. Sia il vincolo di lavoro che il vincolo di materia prima soddisfano il requisito del modello lineare.
I nostri vincoli di domanda hanno la forma di
(Droga 1 prodotta)<=(Domanda di droga 1) (Droga 2 prodotta)<=(Domanda di droga 2) §(Farmaco 6 prodotto)<=(Domanda di droga 6)
Ogni vincolo di domanda soddisfa anche il requisito del modello lineare, perché ognuno viene valutato sommando i termini della maschera (cella modificabile)*(costante) e confrontando le somme con una costante.
Avendo dimostrato che il nostro modello di mix prodotto è un modello lineare, perché dovremmo preoccuparci?
-
Se un modello del Risolutore è lineare e selezioniamo Presuppone modello lineare, è garantito che il Risolutore trovi la soluzione ottimale per il modello Risolutore. Se un modello del Risolutore non è lineare, il Risolutore potrebbe trovare o meno la soluzione ottimale.
-
Se un modello risolutore è lineare e selezioniamo Assume modello lineare, il Risolutore utilizza un algoritmo molto efficiente (il metodo simplex) per trovare la soluzione ottimale del modello. Se un modello del Risolutore è lineare e non si seleziona Assume modello lineare, il Risolutore utilizza un algoritmo molto inefficiente (il metodo GRG2) e potrebbe avere difficoltà a trovare la soluzione ottimale del modello.
Dopo aver fatto clic su OK nella finestra di dialogo Opzioni Risolutore, si torna alla finestra di dialogo principale del Risolutore, illustrata in precedenza nella figura 27-7. Quando si fa clic su Risolvi, il Risolutore calcola una soluzione ottimale (se presente) per il modello della combinazione di prodotti. Come ho detto nel Capitolo 26, una soluzione ottimale per il modello di mix prodotto sarebbe un insieme di valori variabili delle celle (libbre prodotte di ogni farmaco) che massimizza il profitto sul set di tutte le soluzioni fattibili. Anche in questo caso, una soluzione fattibile è un insieme di valori di cella variabili che soddisfano tutti i vincoli. I valori variabili delle celle mostrati nella figura 27-9 sono una soluzione fattibile perché tutti i livelli di produzione sono non negativi, i livelli di produzione non superano la domanda e l'uso delle risorse non supera le risorse disponibili.
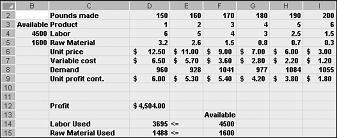
I valori variabili delle celle illustrati nella figura 27-10 nella pagina successiva rappresentano una soluzione non fattibile per i motivi seguenti:
-
Produciamo più di Droga 5 che la domanda per esso.
-
Usiamo più lavoro di quello disponibile.
-
Usiamo più materie prime di quelle disponibili.
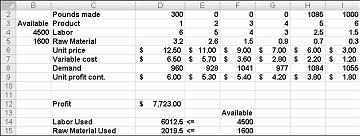
Dopo aver fatto clic su Risolvi, il Risolutore trova rapidamente la soluzione ottimale illustrata nella figura 27-11. È necessario selezionare Mantieni soluzione risolutore per mantenere i valori ottimali della soluzione nel foglio di lavoro.
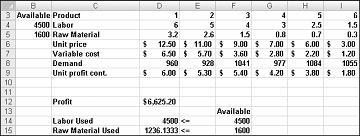
La nostra società di droga può massimizzare il suo profitto mensile ad un livello di $6.625.20 producendo 596.67 libbre di Droga 4, 1084 libbre di Droga 5, e nessuno degli altri farmaci! Non è possibile determinare se è possibile ottenere il profitto massimo di 6.625,20 dollari in altri modi. Tutto quello di cui possiamo essere sicuri è che con le nostre risorse limitate e la nostra domanda, non c'è modo di fare più di $ 6,627,20 questo mese.
Si supponga che la domanda per ogni prodotto debba essere soddisfatta. Vedere il foglio di lavoro Nessuna soluzione fattibile nel file Prodmix.xlsx. È quindi necessario modificare i vincoli della domanda da D2:I2<=D8:I8 a D2:I2>=D8:I8. A questo scopo, aprire il Risolutore, selezionare il vincolo D2:I2<=D8:I8 e quindi fare clic su Cambia. Viene visualizzata la finestra di dialogo Modifica vincolo, illustrata nella figura 27-12.
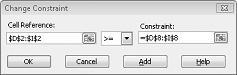
Selezionare >=, quindi fare clic su OK. Abbiamo fatto in modo che il Risolutore consideri la possibilità di modificare solo i valori delle celle che soddisfano tutte le richieste. Quando si fa clic su Risolvi, viene visualizzato il messaggio "Il Risolutore non è riuscito a trovare una soluzione fattibile". Questo messaggio non significa che abbiamo commesso un errore nel nostro modello, ma piuttosto che con le nostre risorse limitate, non possiamo soddisfare la domanda di tutti i prodotti. Il Risolutore ci sta semplicemente dicendo che se vogliamo soddisfare la domanda di ogni prodotto, dobbiamo aggiungere più lavoro, più materie prime o più di entrambi.
Vediamo cosa succede se consentiamo una domanda illimitata per ogni prodotto e consentiamo la produzione di quantità negative di ogni farmaco. Questo problema del Risolutore è visualizzato nel foglio di lavoro Imposta valori non convergenti nel file Prodmix.xlsx. Per trovare la soluzione ottimale per questa situazione, aprire il Risolutore, fare clic sul pulsante Opzioni e deselezionare la casella Presuppone non negativo. Nella finestra di dialogo Parametri Risolutore selezionare il vincolo di richiesta D2:I2<=D8:I8 e quindi fare clic su Elimina per rimuovere il vincolo. Quando si fa clic su Risolvi, il Risolutore restituisce il messaggio "Imposta valori cella non convergenti". Questo messaggio indica che se la cella di destinazione deve essere ingrandita (come nell'esempio), esistono soluzioni fattibili con valori arbitrariamente grandi delle celle di destinazione. Se la cella di destinazione deve essere ridotta a icona, il messaggio "Impostare i valori delle celle non convergenti" significa che esistono soluzioni fattibili con valori arbitrariamente piccoli delle celle di destinazione. Nella nostra situazione, consentendo la produzione negativa di un farmaco, in effetti "creiamo" risorse che possono essere utilizzate per produrre arbitrariamente grandi quantità di altri farmaci. Data la nostra domanda illimitata, questo ci permette di fare profitti illimitati. In una situazione reale, non possiamo fare una quantità infinita di soldi. In breve, se viene visualizzato "Imposta valori non convergere", il modello presenta un errore.
-
Si supponga che la nostra società di farmaci possa acquistare fino a 500 ore di lavoro a $ 1 in più all'ora rispetto ai costi attuali del lavoro. Come si può massimizzare il profitto?
-
In uno stabilimento di produzione di chip quattro tecnici (A, B, C e D) producono tre prodotti (prodotti 1, 2 e 3). Questo mese, il produttore del chip può vendere 80 unità di Prodotto 1, 50 unità di Prodotto 2, e al massimo 50 unità di Prodotto 3. Il tecnico A può fare solo i prodotti 1 e 3. Il tecnico B può fare solo i prodotti 1 e 2. Il tecnico C può realizzare solo il Prodotto 3. Il tecnico D può realizzare solo il Prodotto 2. Per ogni unità prodotta, i prodotti contribuiscono al seguente profitto: Prodotto 1, $6; Prodotto 2, $7; e prodotto 3, $ 10. Il tempo (in ore) di cui ogni tecnico ha bisogno per fabbricare un prodotto è il seguente:
Prodotto
Tecnico A
Tecnico B
Tecnico C
Tecnico D
1
2
2,5
Operazione non possibile
Operazione non possibile
2
Operazione non possibile
3
Operazione non possibile
3,5
3
3
Operazione non possibile
4
Operazione non possibile
-
Ogni tecnico può lavorare fino a 120 ore al mese. In che modo il produttore del chip può massimizzare il suo profitto mensile? Si supponga di poter produrre un numero frazionario di unità.
-
Uno stabilimento di produzione di computer produce mouse, tastiere e joystick per videogiochi. Il profitto unitario, l'utilizzo del lavoro per unità, la domanda mensile e l'utilizzo del tempo macchina per unità sono indicati nella tabella seguente:
Mouse
Tastiere
Joystick
Profitto/unità
$ 8
$ 11
9 $
Uso del lavoro/unità
0,2 ore
0,3 ore
0,24 ore
Tempo macchina/unità
0,04 ore
0,055 ora
0,04 ore
Domanda mensile
15.000
27,000
11,000
-
Ogni mese sono disponibili in totale 13.000 ore di lavoro e 3.000 ore di tempo della macchina. Come può il produttore massimizzare il suo contributo mensile di profitto dallo stabilimento?
-
Risolvere il nostro esempio di droga presupponendo che una domanda minima di 200 unità per ogni farmaco deve essere soddisfatto.
-
Jason fa braccialetti a diamante, collane e orecchini. Vuole lavorare un massimo di 160 ore al mese. Ha 800 once di diamanti. Il profitto, il tempo di lavoro e le once di diamanti necessari per produrre ogni prodotto sono indicati di seguito. Se la domanda per ogni prodotto è illimitata, come può Jason massimizzare il suo profitto?
Prodotto
Utile unitario
Ore di lavoro per unità
Once di diamanti per unità
Braccialetto
€ 300
.35
1,2
Collana
€ 200
.15
.75
Orecchini
€ 100
5%
.5










