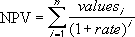NPV 関数

構文

NPV(rate,value1,value2,..)

利率     は、1 期間の間の割引率です。

Value1、value2,...     は、支払いと収入を表す 1 から 29 の引数です。 Value1、value2,...は、各期間の終了時に等間隔で実行する必要があります。 NPVでは、value1、value2 の順序が使用されます,...を使用してキャッシュ フローの順序を解釈します。 支払額と収益額を入力する際は、その順序に注意してください。 数値、空、論理値、または数値のテキスト表現である引数はカウントされます。エラー値または数値に変換できないテキストである引数は無視されます。

解説

• NPV 関数では、投資は値 1 のキャッシュ フローが発生する日付より 1 期前に開始され、引数リストの最後のキャッシュ フローで終了します。 NPV 関数の計算は、将来のキャッシュ フローに基づいて行われます。 このため、最初のキャッシュ フローが 1 期目の期首に発生する場合、このキャッシュ フローを引数として指定せずに、NPV 関数の計算結果に加算する必要があります。 詳細については、使用例を参照してください。

• n が引数リスト内のキャッシュ フロー数の場合、NPV 関数は、次の数式で表されます。

  

• NPV 関数は、投資の現在価値を返す PV 関数と似ています。 PV 関数と NPV 関数の最も大きな違いは、PV 関数ではキャッシュ フローが期首と期末のどちらに発生してもかまわない点にあります。 また、NPV 関数ではキャッシュ フローの金額が一定していませんが、PV 関数では投資期間を通じて一定である必要があります。 財務関数の詳細については、PV 関数を参照してください。

使用例 1

次の例では、

• レート は年間割引率です。

• Value1 は、今日から 1 年間の投資の初期コストです。

• Value2 は、最初の年からの戻り値です。

• Value3 は、2 年目からの戻り値です。

• Value4 は、3 年目からの戻り値です。

この例では、最初の期間の終了時に支払いが行われるため、最初の 10,000 ドルのコストを値の 1 つとして含めます。

使用例 2

次の例では、

• レート は年間割引率です。 インフレ率や借入金の利息を考慮した年間割引率。

• Value1 は、今日から 1 年間の投資の初期コストです。

• Value2 は、最初の年からの戻り値です。

• Value3 は、2 年目からの戻り値です。

• Value4 は、3 年目からの戻り値です。

• Value5 は、4 年目からの戻り値です。

• Value6 は、5 年目からの戻り値です。

この例では、最初の期間の開始時に支払いが行われるため、最初の 40,000 ドルのコストを値の 1 つとして含めないでください。