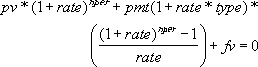PV 関数

構文

PV(rate,nper,pmt,fv,type)

利率     は、期間あたりの金利です。 たとえば、年利 10% の自動車ローンを利用して月払いで返済を行う場合、月単位の金利は 10%/12 = 0.83% となります。 この場合、数式には 10%/12、0.83%、または 0.0083 の形式で指定します。

期間     は、年金の支払期間の合計数です。 たとえば、4 年ローンを利用して月払いで返済を行う場合、このローンの支払回数は 4*12 = 48 となります。 この場合、数式には 48 の形式で指定します。

Pmt     は、各期間に行われた支払いであり、年金の有効期間中に変更することはできません。 通常、pmt には元金と利息が含まれますが、その他の手数料や税金は含まれていません。 たとえば、10,000 ドル、4 年の自動車ローンの 12% での毎月の支払いは$263.33 です。 pmt として数式に「-263.33」と入力します。 pmt を省略する場合は、fv 引数を含める必要があります。

将来価値     は、将来の価値、または最後の支払いが行われた後に達成する現金残高です。 将来価値を省略すると、0 を指定したと見なされます (たとえば、ローンなどの借入金の将来価値は 0 になります)。 たとえば、18 年間で 500 万円をためることを目標にした場合、この投資の将来価値は 500 万円になります。 投資期間の金利を予測することにより、毎月の貯蓄額を決めることができます。 将来価値を省略した場合は、定期支払額を必ず指定してください。

型     は 0 または 1 の数値で、支払い期限を示します。

解説

• 利率と期間内支払回数を指定するときは、時間単位を一致させる必要があります。 たとえば、年利 12% の 4 年ローンを月払いで返済する場合、利率には 12%/12 = 1 (%) を、期間内支払回数には 4*12 = 48 (月) を指定します。 また、これと同じローンを年払いで返済する場合は、利率に 12 (%)、期間内支払回数に 4 (年) を指定します。

• 年金には次の関数が適用されます。IPMT。PMT。PPMT。PV;と RATE。 これらの関数の対象となる投資は、定額の支払いが定期的に行われることが前提になっています。 たとえば、自動車ローンや不動産ローンなどが投資の対象になります。 詳細については、各関数の説明を参照してください。

• 投資関数では、定額預金の支払いのような出金は負の数で表し、配当金のような入金は正の数で表します。 たとえば、銀行口座の預金 10 万円を引数として使用する場合、預金者側は -100000、銀行側では 100000 と指定します。

• 1 つの財務上の議論は、他の点で解決されます。 たとえば、利率が 0 でない場合は、次の数式が成立します。

  

  利率 = 0 の場合は、次の数式が成立します。

  (定額支払額 * 期間) + 現在価値 + 将来価値 = 0

例

次の例では、

• Pmt は、毎月末に保険年金から支払われるお金です。

• レート は、支払ったお金で得られた金利です。

• Nper は、お金が支払われる年です。

金利を 12 で割って毎月のレートを取得します。 お金が支払われる年には、支払いの数を取得するために 12 が乗算されます。

結果は負の値になります。これは、支払うお金、つまり支払うキャッシュ フローを表しているためです。 年金の支払い (60,000) を求められた場合は、年金の現在の価値 (59,777.15) が支払いを求められる金額よりも小さいため、これは適切な投資にならないと判断されます。