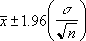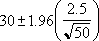Grąžina generalinės aibės vidurkio pasikliautinąjį intervalą su normaliuoju skirstiniu. Patikimumo intervalas yra diapazonas abiejose pavyzdžio vidurkio pusėse. Pavyzdžiui, jei užsisakote produktą paštu, galite, esant tam tikram patikimumo lygiui, nustatyti anksčiausią ir naujausią produktą.
Sintaksė
CONFIDENCE(alfa,standard_dev,dydis)
Alfa reikšmingumo lygis, naudojamas patikimumo lygiui apskaičiuoti. Patikimumo lygis, lygus 100*(1 - alfa)%, arba, kitaip sakant, 0,05 reikšmės alfa rodo 95 procentų patikimumo lygį.
Standart_nuokr yra duomenų diapazono aibės standartinis nuokrypis ir laikoma, kad jis žinomas.
Dydis yra imties dydis.
Pastabos
-
Jei bet kuris argumentas nėra skaičius, CONFIDENCE grąžins #VALUE! klaidos reikšmę.
-
Jei alfa ≤ 0 arba alfa ≥ 1, CONFIDENCE grąžins #NUM! klaidos reikšmę.
-
Jei standard_dev ≤ 0, CONFIDENCE grąžins #NUM! klaidos reikšmę.
-
Jei dydis yra ne sveikasis skaičius, trupmeninė jo dalis atmetama.
-
Jei dydis < 1, CONFIDENCE grąžins #NUM! klaidos reikšmę.
-
Jei daroma prielaida, kad alfa lygu 0,05, reikia apskaičiuoti sritį, kurią riboja standartinė įprastinė kreivė (1 – alfa) arba 95 procentai. Ši reikšmė yra ± 1,96. Todėl patikimumo intervalas yra:
Pavyzdys
Tarkime, kad mūsų 50 įvažiavimo į darbą imties atveju vidutinė kelionės į darbą trukmė yra 30 minučių, o aibės standartinis nuokrypis yra 2,5. Galime būti 95 procentai įsitikinę, kad aibės vidurkis yra intervale:
|
Alfa |
Standartinis nuokrypis nuo standartinio nuokrypio |
Dydis |
Formulė |
Aprašas (rezultatas) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENCE([Alfa],[StdDev],[Dydis]) |
Aibės vidurkio patikimumo intervalas. Kitaip tariant, vidutinis kelionės į darbą ilgis yra 30 ± 0,692951 minutės arba 29,3–30,7 minutės. (0.692951) |