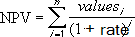NPV (funkcija NPV)

Sintaksė

NPV(norma,reikšmė1,reikšmė2,...)

Norma     nuolaidos norma per vieną laikotarpį.

Reikšmė1, reikšmė2,...     yra nuo 1 iki 29 argumentų, nurodančių mokėjimus ir pajamas. Reikšmė1, reikšmė2,... turi būti išdėstyti vienodais intervalais per tam tikrą laiką ir atsirasti kiekvieno laikotarpio pabaigoje. NPV naudoja reikšmės1, reikšmės2 tvarką,... pinigų srautų eilės tvarką. Įsitikinkite, kad įvedėte mokėjimo ir įplaukų vertes teisinga eilės tvarka. Skaičiuojami argumentai, kurie yra skaičiai, tuščios, loginės reikšmės arba tekstinės skaičių reprezentacijos; argumentai, kurie yra klaidos reikšmės, arba tekstas, kurio negalima perskaičiuoti į skaičius, nepaisomas.

Pastabos

• Funkcijos NPV investavimas prasideda vieną laikotarpį anksčiau prieš pinigų srauto reikšmės1 datą ir baigiasi su paskutiniu sąraše esančiu pinigų srautu. Funkcijos NPV skaičiavimai remiasi būsimu pinigų srautu. Jei jūsų pirmas pinigų srautas yra pirmojo laikotarpio pradžioje, pirmoji reikšmė turi papildyti neįtrauktą į reikšmių argumentus NPV rezultatą. Norėdami gauti daugiau informacijos, žiūrėkite žemiau esančius pavyzdžius.

• Jei pinigų srautų skaičius verčių sąraše yra n, funkcijos NVP formulė yra:

  

• Funkcija NPV yra panaši į funkciją PV (present value – dabartinė reikšmė). Pagrindinis skirtumas tarp funkcijos NVP ir funkcijos PV yra tai, kad funkcija PV leidžia, kad pinigų srautas prasidėtų arba laikotarpio pabaigoje, arba pradžioje. Skirtingai nuo nepastovių funkcijos NPV pinigų srautų verčių, funkcijos PV pinigų srautai gali nesikeisti per visą investavimo laikotarpį. Norėdami gauti daugiau informacijos apie metines išmokas ir finansines funkcijas, žiūrėkite PV.

1 pavyzdys

Šiame pavyzdyje:

• Norma yra metinė diskonto norma.

• Reikšmė1 yra pradinė investicijų kaina po metų nuo šiandien.

• Reikšmė2 yra pirmųjų metų grąža.

• Reikšmė3 yra antrųjų metų grąža.

• Reikšmė4 yra trečiųjų metų grąža.

Pateiktame pavyzdyje pradines 10 000 EUR išlaidas įtraukiate kaip vieną iš reikšmių, nes mokėjimas atliekamas pirmojo laikotarpio pabaigoje.

2 pavyzdys

Šiame pavyzdyje:

• Norma yra metinė diskonto norma. Tai gali būti infliacijos procentai arba konkuruojančios investicijos diskonto norma.

• Reikšmė1 yra pradinė investicijų kaina po metų nuo šiandien.

• Reikšmė2 yra pirmųjų metų grąža.

• Reikšmė3 yra antrųjų metų grąža.

• Reikšmė4 yra trečiųjų metų grąža.

• Reikšmė5 yra ketvirtųjų metų grąža.

• Reikšmė6 yra penktųjų metų grąža.

Pateiktame pavyzdyje pradinių 40 000 EUR išlaidų neįtraukiate kaip vienos iš reikšmių, nes mokėjimas atliekamas pirmojo laikotarpio pradžioje.