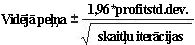Šo rakstu adaptēja Wayne L. Winston un Microsoft Excel datu analīzes un biznesa modelēšanas programma.
-
Kas izmanto Monte Kārcijas simulāciju?
-
Kas notiek, šūnā ierakstot =RAND( )
-
Kā simulēt diskrēta nejauša mainīgā vērtības?
-
Kā var simulēt parasta nejauša mainīgā vērtības?
-
Kā apsveikuma kartīšu uzņēmums var noteikt, cik kartīšu ir jāražo?
Mēs vēlos precīzi novērtēt iespējamības, ka neesat pārliecināts par notikumiem. Piemēram, kāda ir varbūtība, ka jaunā produkta naudas plūsmām būs pozitīva pašreizējā neto vērtība (NPV)? Kāds ir mūsu investīciju portfeļa riska faktors? Monte imitācija ļauj mums modelēt situācijas, kas rada neskaidrību, un pēc tam tās nomāc datorā tūkstošiem reižu.
Piezīme.: Nosaukumu Monte Ardo simulāciju nodrošina datora simulācijas, kas tika veiktas 1930. un 1940. gadā, lai aprēķinātu varbūtību, ka ķēde, kas nepieciešama atoma nomācības detonācijai, veiksmīgi darbojas. Šajā darbā iesaistīs fizikisti, tāpēc tiem bija jābrauc ar koda nosaukumu Monte Ābe.
Nākamajās piecās nodaļās jūs redzēsit piemērus tam, kā varat izmantot programmu Excel, lai veiktu Monte Kārņu simulācijas.
Daudzos uzņēmumos Monte Aramā simulācija tiek izmantota kā svarīga viņu lēmumu pieņemšanas procesa daļa. Daži piemēri.
-
General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb, and Eli Lilly use simulation to estimate the average return and the risk factor of new products. GM šo informāciju izmanto uzņēmuma vadītājs, lai noteiktu, kuri produkti tiek laisti tirgū.
-
GM izmanto simulāciju darbībām, piemēram, uzņēmuma ienākumu prognozēšanai pēc neto ienākumiem, strukturālajām un iegādes izmaksām, kā arī nosaka tā redzamību dažādiem riska veidiem (piemēram, procentu likmes izmaiņām un valūtas likmes svārstībām).
-
Lilly izmanto simulāciju, lai noteiktu optimālo auga noslodzi katram.
-
Proctor un Gamble izmanto simulāciju, lai modelēt un optimāli hedžēt ārējo exchange risku.
-
Sears izmanto simulāciju, lai noteiktu, cik produkta līnijas vienības jāpakārto no piegādātājiem, piemēram, šogad pasūtīto doku pāru skaitu.
-
Naftas un uzņēmuma uzņēmumi izmanto simulāciju, lai vērtu "reālas opcijas", piemēram, iespējas izvērst, noslēgt līgumu vai atlikt projektu vērtību.
-
Finanšu plānotāji izmanto Monte Kārijas simulāciju, lai noteiktu optimālas investīciju stratēģijas viņu klientu aiziešana no darba.
Ievadot šūnā formulu =RAND( ), tiek iegūts skaitlis, kas, visticamāk, varētu pieņemt jebkuru vērtību no 0 līdz 1. Tādējādi aptuveni 25 procenti no laika ir jābūt skaitlim, kas ir mazāks vai vienāds ar 0,25; Aptuveni 10 procenti no laika iegūstiet skaitli, kas ir vismaz 0,90 utt. Lai parādītu, kā funkcija RAND darbojas, apskatiet faila versiju, Randdemo.xlsx parādīts attēlā 60-1.
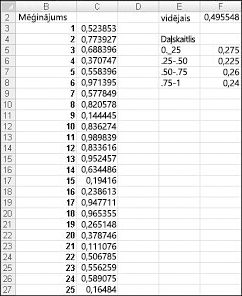
Piezīme.: Atverot faila formātu, Randdemo.xlsx tie paši nejauši izvēlētie skaitļi nebūs redzami attēlā 60-1. Funkcija RAND vienmēr automātiski pārrēķina skaitļus, ko tā ģenerē, atverot darblapu vai ievadot darblapā jaunu informāciju.
Vispirms no šūnas C3 kopējiet šūnā C4:C402 formulu =RAND(). Pēc tam jūs nosauksiet diapazonu C3:C402 Dati. Pēc tam kolonnā F varat noteikt 400 nejauši izvēlētu skaitļu (šūna F2) vidējo vērtību un izmantot funkciju COUNTIF, lai noteiktu daļskaitļus, kas ir no 0 līdz 0,25, 0,25 un 0,50, 0,50 un 0,75, kā arī 0,75 un 1. Nospiežot taustiņu F9, nejauši izvēlētie skaitļi tiek pārrēķināti. Ievērojiet, ka 400 skaitļu vidējā vērtība vienmēr ir aptuveni 0,5, un aptuveni 25 procenti rezultātu tiek iegūti intervālā no 0,25. Šie rezultāti atbilst nejauša skaitļa definīcijai. Ņemiet arī vērā, ka rand ģenerētās vērtības dažādās šūnās ir neatkarīgas. Piemēram, ja šūnā C3 ģenerētais nejaušais skaitlis ir liels skaitlis (piemēram, 0,99), tas nevēsta mums par citu nejauši izvēlētu skaitļu vērtībām.
Pieņemsim, ka kalendāra pieprasījumu nosaka šāds diskrēts gadījuma mainīgais:
|
Pieprasījuma |
Varbūtība |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Kā programma Excel var parādīt vai simulēt šo kalendāru pieprasījumu vairākas reizes? Sarežģītākais ir katras iespējamās funkcijas RAND vērtības saistīšana ar iespējamo kalendāru pieprasījumu. Tālāk minētā piešķiršana nodrošina, ka 10 000 pieprasījumu radīsies 10 procenti no laika utt.
|
Pieprasījuma |
Piešķirts nejauši izvēlēts skaitlis |
|---|---|
|
10 000 |
Mazāks par 0,10 |
|
20 000 |
Lielāks par vai vienāds ar 0,10 un mazāks par 0,45 |
|
40,000 |
Lielāks par vai vienāds ar 0,45 un mazāks par 0,75 |
|
60 000 |
Lielāks par vai vienāds ar 0,75 |
Lai demonstrētu pieprasījuma simulāciju, aplūkojiet failu Discretesim.xlsx, parādīts nākamajā lapā attēlā 60-2.
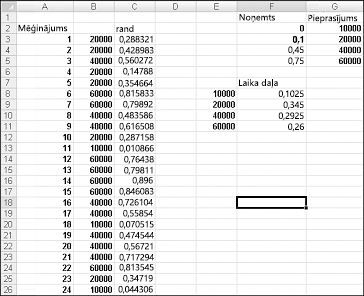
Mūsu simulācijas atslēga ir izmantot gadījumskaitļu, lai uzsāktu uzmeklēšanu no tabulas diapazona F2:G5 ( ar nosaukumu uzmeklēšana). Nejauši izvēlēti skaitļi, kas ir lielāki vai vienādi ar 0 un mazāki par 0,10, radīs pieprasījumu 10 000; nejauši izvēlēti skaitļi, kas ir lielāki vai vienādi ar 0,10 un mazāki par 0,45, nozīmēs, ka pieprasījums ir 20 000; nejauši izvēlēti skaitļi, kas ir lielāki vai vienādi ar 0,45 un mazāki par 0,75, nozīmēs, ka pieprasījums ir 40 000; un nejauši izvēlēti skaitļi, kas lielāki vai vienādi ar 0,75, nozīmē, ka pieprasījums ir 60 000. Tiek ģenerēti 400 nejauši izvēlēti skaitļi, kopējot no C3 uz C4:C402 formulu RAND(). Pēc tam ģenerējiet kalendāra pieprasījuma 400 mēģinājumus vai iterācijas, kopējot no B3 uz B4:B402 formulu VLOOKUP(C3,uzmeklēšana,2). Šī formula nodrošina, ka jebkurš gadījumskaitļi, kas ir mazāki par 0,10, ģenerē 10 000 pieprasījumu, jebkurš gadījumskaitļi diapazonā no 0,10 līdz 0,45 ģenerē 20 000 pieprasījumu utt. Šūnu diapazonā F8:F11 izmantojiet funkciju COUNTIF, lai noteiktu 400 iterāciju daļu, kas dod katra pieprasījuma vērtību. Kad nospiežam taustiņu F9, lai pārrēķinātu nejauši izvēlētus skaitļus, simulētās varbūtības ir tuvu mūsu pieņemtajām pieprasījuma varbūtībām.
Ja ievadīsiet jebkurā šūnā formulu NORMINV(rand(),mu,sigma), tiks ģenerēta normāla gadījuma mainīgā simulēta vērtība ar vidējo mu un standartnovirzes sigmu. Šī procedūra ir ilustrēta failu Normalsim.xlsx, kā parādīts attēlā 60-3.
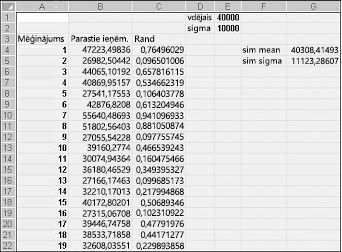
Pieņemsim, ka mēs vēlamies simulēt 400 mēģinājumus jeb iterācijas parastam gadījuma mainīgajam ar vidējo vērtību 40 000 un standartnovirzi 10 000. (Šīs vērtības var ierakstīt šūnās E1 un E2, un šīs šūnas attiecīgi var nosaukt vidējo unsigma.) Kopējot formulu =RAND() no C4 uz C5:C403, tiek ģenerēti 400 dažādi nejauši izvēlēti skaitļi. Kopējot no B4 uz B5:B403 formulu NORMINV(C4,mean,sigma) ģenerē 400 dažādas mēģinājuma vērtības no normāla gadījuma mainīgā ar vidējo vērtību 40 000 un standartnovirzi 10 000. Nospiežot taustiņu F9, lai pārrēķinātu nejauši izvēlētus skaitļus, vidējais paliek tuvu 40 000 un standartnovirze ir tuvu 10 000.
Būtībā nejaušam skaitlim x formula NORMINV(p,mu,sigma) ģenerē normāla nejauša mainīgā p-toprocentili ar vidējo mu un standartnovirzes sigmu. Piemēram, gadījumskaitli 0,77 šūnā C4 (sk. attēlu 60-3) ģenerē šūnā B4, kas ir aptuveni 77. procentile no normāla gadījuma mainīgā ar vidējo vērtību 40 000 un standartnovirzi 10 000.
Šajā sadaļā jūs redzēsit, kā Monte Kausa simulāciju var izmantot kā lēmumu pieņemšanas rīku. Pieņemsim, ka Valentīna dienas kartītes pieprasījumu nosaka šāds diskrēts mainīgais:
|
Pieprasījuma |
Varbūtība |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Apsveikuma kartīte pārdota par 4,00 USD, un katras kartītes ražošanas mainīgās izmaksas ir 1,50 EUR. Izmantojot kreisās kartes, no tās ir atbrīvoties par 0,20 USD vienai kartei. Cik kartīšu ir jādrukā?
Būtībā mēs simulējam katru iespējamo ražošanas daudzumu (10 000, 20 000, 40 000 vai 60 000) bieži (piemēram, 1000 iterācijas). Pēc tam tiek noteikts, kurš pasūtījumu skaits iegūst maksimālo vidējo peļņu 1000 iterācijās. Šīs sadaļas datus varat atrast faila failā, Valentine.xlsx parādīts attēlā 60-4. Šūnu diapazonā B1:B11 diapazonu nosaukumi tiek piesaistīti šūnām C1:C11. Šūnu diapazonam G3:H6 tiek piešķirta nosaukuma uzmeklēšana. Mūsu pārdošanas cenu un izmaksu parametri tiek ievadīti šūnās C4:C6.
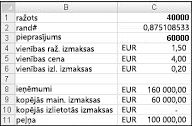
Var ievadīt izmēģinājuma ražošanas daudzumu (šajā piemērā 40 000) šūnā C1. Pēc tam izveidojiet nejauši izvēlētu skaitli šūnā C2 ar formulu =RAND(). Kā aprakstīts iepriekš, tiek simulēts kartītes pieprasījums šūnā C3 ar formulu VLOOKUP(rand,uzmeklēšana,2). (VLOOKUP formulā rand ir šūnas nosaukums, kas piešķirts šūnai C3, nevis funkcija RAND.)
Pārdoto vienību skaits ir mazākais no mūsu ražošanas daudzuma un pieprasījuma. Šūnā C8 aprēķināt mūsu ieņēmumus, izmantojot formulu MIN(saražotais,pieprasījums)*unit_price. Šūnā C9 tiek aprēķinātas kopējās ražošanas izmaksas, izmantojot formulu , kas saražota*unit_prod_cost.
Ja mēs sagatavojam vairāk karšu, nekā ir pēc pieprasījuma, to vienību skaits, kas lielākas par ražošanas apjomu mīnus pieprasījums; pretējā gadījumā neviena cita mērvienība netiek atstāta. Mēs izskaitļojam mūsu nomācīgās vērtības šūnā C10, izmantojot formulu unit_disp_cost*IF(>pēc pieprasījuma,ražošanas–pieprasījums,0). Visbeidzot šūnā C11 mēs aprēķinām savu peļņu kā ieņēmumus total_var_cost-total_disposing_cost.
Mēs vēlos izmantot efektīvu veidu, lai nospiestu taustiņu F9 vairākas reizes (piemēram, 1000) katrai ražošanas daudzumam un kas balstīts uz paredzēto peļņu katram daudzumam. Šādā situācijā mūsu palīgā nāk divvirzienu datu tabula. (Detalizētu informāciju par datu tabulām skatiet 15. nodaļā "Sensitivitātes analīze ar datu tabulām".) Šajā piemērā izmantotā datu tabula ir parādīta 60.–5. attēlā.
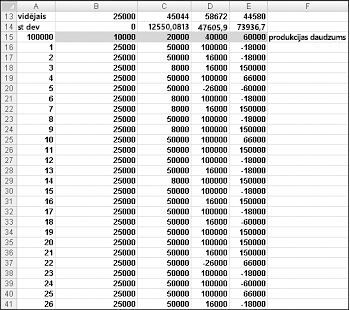
Šūnu diapazonā A16:A1015 ievadiet skaitļus 1–1000 (atbilstoši mūsu 1000 mēģinājumiem). Vienkāršs veids, kā izveidot šīs vērtības, ir ievadīt šūnā A16 ievadot vērtību 1. Atlasiet šūnu un pēc tam cilnes Sākums grupā Rediģēšana noklikšķiniet uz Aizpildījums un atlasiet Sērijas, lai parādītu dialoglodziņu Sērijas. Sērijas dialoglodziņā , kas parādīts attēlā 60-6, ievadiet darbības vērtību 1 un apturēšanas vērtību 1000. Apgabalā Sērijas šeit atlasiet opciju Kolonnas un pēc tam noklikšķiniet uz Labi. Skaitļi no 1 līdz 1000 tiks ievadīti kolonnā A, sākot ar šūnu A16.
Pēc tam ievadām iespējamos ražošanas apjomus (10 000, 20 000, 40 000, 60 000) šūnās B15:E15. Mēs vēlamies aprēķināt peļņu katram izmēģinājuma skaitlim (no 1 līdz 1000) un katram ražošanas daudzumam. Mēs atsaucaties uz peļņas formulu (aprēķināta šūnā C11) mūsu datu tabulas augšējā kreisajā šūnā (A15), ievadot =C11.
Tagad esam gatavi apmānīt Excel, simulējot 1000 iterācijas pieprasījuma katram ražošanas daudzumam. Atlasiet tabulas diapazonu (A15:E1014) un cilnes Dati grupā Datu rīki noklikšķiniet uz Ko darīt, ja analīze un pēc tam atlasiet Datu tabula. Lai iestatītu divvirzienu datu tabulu, kā rindas ievades šūnu izvēlieties mūsu ražošanas daudzumu (šūna C1) un kā kolonnas ievades šūnu atlasiet jebkuru tukšu šūnu (izvēlējāmies šūnu I14). Pēc noklikšķināšanas uz Labi programma Excel simulē 1000 pieprasījuma vērtības katram pasūtījumu daudzumam.
Lai saprastu, kāpēc tas darbojas, apsveriet iespēju šūnu diapazonā C16:C1015 novietotās datu tabulas vērtības. Katrai no šīm šūnām Excel šūnā C1 izmantos vērtību 20 000. Šūnā C16 kolonnas ievades šūnas vērtība 1 tiek ievietota tukšā šūnā, un nejauši izvēlētie skaitļi šūnā C2 tiek pārrēķināti. Pēc tam šūnā C16 tiek ierakstīta atbilstošā peļņa. Pēc tam kolonnas šūnas ievades vērtība 2 tiek ievietota tukšā šūnā, un gadījumskaitļi šūnā C2 atkal tiek pārrēķināti. Atbilstošā peļņa tiek ievadīta šūnā C17.
Kopējot no šūnas B13 uz C13:E13 formulu AVERAGE(B16:B1015), tiek aprēķināta katra ražošanas daudzuma vidējā simulētā peļņa. Kopējot no šūnas B14 uz C14:E14 formulu STDEV(B16:B1015), katram pasūtījumu daudzumam tiek aprēķināta mūsu simulētās peļņas standartnovirze. Ikreiz, kad mēs nospiežam taustiņu F9, katram pasūtījumu daudzumam tiek simulētas 1000 pieprasījuma iterācijas. 40 000 kartīšu ražošanas laikā vienmēr tiek gūta lielākā paredzētā peļņa. Tāpēc tiek parādīts, ka 40 000 kartīšu ražošanas mērķis ir 40 000 vizītkartes.
The Impact of Risk on Our Decision Ja 40 000 kartīšu vietā tika iegūtas 20 000 kartītes, mūsu prognozētā peļņa samazinās aptuveni 22%, bet mūsu risks (jāmēra ar peļņas standartnovirzi) samazinās gandrīz 73 procenti. Tāpēc, ja esam ļoti apgriezti pret risku, 20 000 kartīšu ražošanas var būt pareizais lēmums. Incidentā, veidojot 10 000 vizītkartes, standartnovirze vienmēr ir 0 vizītkartes, jo, ja izveidosim 10 000 kartes, tās vienmēr tiks pārdotas bez aizgādēm.
Piezīme.: Šajā darbgrāmatā opcija Aprēķins ir iestatīta uz Automātiski , izņemot tabulām. (Izmantojiet komandu Aprēķins, kas atrodas cilnes Formulas grupā Aprēķins.) Šis iestatījums nodrošina, ka mūsu datu tabula netiks pārrēķināta, ja vien nenospiežam taustiņu F9, kas ir laba ideja, jo liela datu tabula palēnina darbu, ja to pārrēķināsiet ikreiz, kad kaut ko ievadāt darblapā. Ņemiet vērā, ka šajā piemērā, nospiežot taustiņu F9, mainīsies vidējā peļņa. Tā notiek tāpēc, ka ikreiz, kad nospiežat taustiņu F9, tiek izmantota 1000 nejauši izvēlētu skaitļu atšķirīga secība, lai ģenerētu pieprasījumus katram pasūtījumu daudzumam.
Vidējās peļņas ticamības intervāls Dabisks jautājums, kas šādā situācijā ir, kādā intervālā esam 95 procenti, vai patiesā vidējā peļņa atstās? Šo intervālu sauc par 95% ticamības intervālu vidējā peļņai. 95 procentu ticamības intervālu simulācijas izvades vidējām aprēķina ar šādu formulu:
Šūnā J11 tiek aprēķināta zemākā robeža 95% ticamības intervālam, ja ir iegūta 40 000 kalendāru ar formulu D13-1.96*D14/SQRT(1000). Šūnā J12 tiek aprēķināta augšējā ticamības intervāla robeža, izmantojot formulu D13+1.96*D14/SQRT(1000). Šie aprēķini tiek parādīti 60.–7. attēlā.
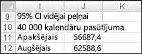
Mēs 95 procentus esam pārliecināti, ka mūsu vidējā peļņa, kad ir pasūtīti 40 000 kalendāri, ir no 56 687 LĪDZ 62 589 EUR.
-
GMC konfiets uzskata, ka pieprasījums pēc 2005. gada envoys parasti tiek sadalīts ar vidējo vērtību 200 un standartnovirzi 30. Viņa envoy saņemšanas izmaksas ir 25 000 EUR, un viņš pārdod envoy par 40 000 EUR. Pusi no visiem envoys, kas nav pārdoti par pilnu cenu, var pārdot par 30 000 EUR. Viņš apsver pasūtījumu 200, 220, 240, 260, 280 vai 300 envoys. Cik viņam viņš jāpas pasūta?
-
Neliels ciems mēģina noteikt, cik žurnāla personas to secību nedēļā. Viņu pieprasījums pēc personas tiek pārvaldīts, izmantojot šādus diskrētus nejaušus mainīgos:
Pieprasījuma
Varbūtība
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Veikals samaksā 1,00 ASV dolārus par katru personas un pārdod to par 1,95 ASV dolāriem. Katru nepiedauto kopiju var atgriezt par 0,50 USD. Cik kopiju personas jāveic veikala pasūtījums?
Vai nepieciešama papildu palīdzība?
Vienmēr varat pajautāt speciālistam Excel tech kopienā vai saņemt atbalstu kopienās.