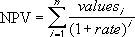NPV (funkcija NPV)

Sintakse

NPV(likme,vērtība1,vērtība2,...)

Likme     ir diskonta likme viena perioda garumā.

Vērtība1, vērtība2,...     ir argumenti no 1 līdz 29, kuri norāda maksājumus un ienākumus. Vērtība1, vērtība2,... jābūt vienmērīgi sadalītām laikā un jābeidzas katra perioda beigās. NPV izmanto vērtība1, vērtība2 secību,... , lai interpretētu naudas plūsmu secību. Pārliecinieties, vai maksājumu un ienākumu vērtības tiek ievadītas pareizā secībā. Tiek skaitīti argumenti, kas ir skaitļi, tukšas, loģiskās vērtības vai tekstuāls skaitļu atspoguļojums; argumenti, kas ir kļūdu vērtības vai teksts, ko nevar pārvērst par skaitļiem, tiek ignorēti.

Piezīmes

• NPV investīcija sākas vienu periodu pirms vērtības1 naudas plūsmas datuma un beidzas ar pēdējo naudas plūsmu sarakstā. NPV aprēķins balstās uz turpmākajām naudas plūsmām. Ja pirmā naudas plūsma parādās pirmā perioda beigās, tad pirmā vērtība ir jāpievieno NPV rezultātam, neiekļaujot vērtību argumentos. Papildinformāciju meklējiet turpmākajos piemēros.

• Ja n ir vērtību saraksta naudas plūsmu skaits, tad NPV formula ir:

  

• Funkcija NPV ir līdzīga funkcijai PV (pašreizējā vērtība). Galvenā atšķirība starp funkcijām PV un NPV ir tāda, ka PV atļauj naudas plūsmām sākties vai nu perioda sākumā, vai beigās. Atšķirībā no mainīgajām funkcijas NPV naudas plūsmu vērtībām funkcijas PV naudas plūsmām investīciju perioda laikā ir jābūt nemainīgām. Informāciju par anuitātēm un finanšu funkcijām skatiet pie funkcijas PV.

1. piemērs

Šajā piemērā:

• Likme ir diskonta gada likme.

• Vērtība1 ir investīciju sākotnējā vērtība pēc viena gada no šodienas.

• Vērtība2 ir pirmā gada ienākumi.

• Vērtība3 ir otrā gada ienākumi.

• Vērtība4 ir trešā gada ienākumi.

Šajā piemērā kā vienu no vērtībām tiek iekļautas sākotnējās 10 000 $ izmaksas, jo maksājums tiek veikts pirmā perioda beigās.

2. piemērs

Šajā piemērā:

• Likme ir diskonta gada likme. Var atspoguļot inflācijas līmeni vai konkurējošās investīcijas procentu likmi.

• Vērtība1 ir investīciju sākotnējā vērtība pēc viena gada no šodienas.

• Vērtība2 ir pirmā gada ienākumi.

• Vērtība3 ir otrā gada ienākumi.

• Vērtība4 ir trešā gada ienākumi.

• Vērtība5 ir ienākumi ceturtajā gadā.

• Vērtība6 ir piektā gada ienākumi.

Šajā piemērā nav iekļautas sākotnējās 40 000 $ izmaksas kā viena no vērtībām, jo maksājums tiek veikts pirmā perioda sākumā.