Svarīgi!: Atbalsts programmai Office 2016 un Office 2019 tika pārtraukts 2025. gada 14. oktobrī. Jauniniet uz Microsoft 365, lai strādātu jebkur no jebkuras ierīces un turpinātu saņemt atbalstu. Iegūt Microsoft 365
Šajā rakstā ir aprakstīta Risinātāja — Microsoft Excel pievienojumprogrammas — izmantošana iespēju analīzei, lai noteiktu optimālu produktu kombināciju.
Kā varu noteikt ikmēneša produktu kombināciju, kas maksimizē peļņu?
Uzņēmumiem bieži vien ir jānosaka katra produkta daudzums, kas tiek reizi mēnesī. Vienkāršākā formā problēma saistībā ar produktu sajaukums ietver to, kā noteikt katra produkta apjomu, kas jāražo mēneša laikā, lai palielinātu peļņu. Produktu kombinācijai parasti ir jāievēro šādi ierobežojumi:
-
Produktu kombinācija nevar izmantot vairāk resursu, nekā ir pieejams.
-
Katram produktam ir ierobežots pieprasījums. Mēs nevaram iegūt vairāk produkta mēneša laikā, nekā pieprasa diktēt, jo liekā ražošana tiek netērēta (piemēram, āmīlīga druka).
Tagad atrisināsim tālāk norādīto produktu kombinācijas problēmas piemēru. Šīs problēmas risinājumu varat atrast faila failā Prodmix.xlsx, parādīts attēlā 27-1.
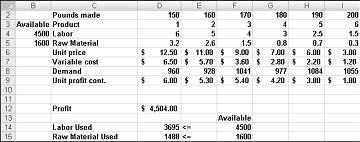
Pieņemsim, ka mēs strādājam pie uzņēmuma, kas savu augu veido sešus atšķirīgus produktus. Katra produkta ražošanā ir nepieciešams āā produktu un neapstrādātu materiālu. 27.–1. attēlā 4. rindā redzamas katram produktam nepieciešamās stundas, lai iegūtu mārciņas katra produkta, un 5. rindā redzamas neapstrādātu materiālu mārciņas, kas nepieciešamas katra produkta mārciņas produktā. Piemēram, lai produktīvi iegūtu mārciņas 1. produktu, nepieciešamas sešas stundas produkta un 3,2 mārciņas neapstrādāta materiāla. Katrā mārciņas cena ir norādīta 6. rindā, vienības maksa par mārciņas vienību ir norādīta 7. rindā, bet peļņa par mārciņas vienību ir norādīta 9. rindā. Piemēram, 2. produkts pārdots par 11,00 ASV dolāriem par mārciņas, rodas 5,70 EUR vienības maksa par mārciņu, bet peļņa par mārciņu iet 5,30 EUR. Mēneša pieprasījums par katru ālandi tiek dots 8. rindā. Piemēram, pieprasījums pēc 3. produkta ir 1041 mārciņa. Šajā mēnesī ir pieejamas 4500 stundas atkva un 1600 mārciņas neapstrādātu materiālu. Kā šis uzņēmums var maksimizēt savu mēneša peļņu?
Ja mēs nedarījām neko par Excel risinātāju, mēs uzsācām šai problēmai uzbrukumā, veidojot darblapu, lai sekotu peļņai un resursu lietojumam, kas saistīts ar produktu sajaukums. Pēc tam mēs izmantosim izmēģinājumversiju un kļūdu, lai variēs produkta kombinācija un optimizētu peļņu, neizmantojot vairāk neapstrādātu materiālu nekā ir pieejams, un nedublējot lieko pieprasījumu. Šajā procesā risinātāju izmantojam tikai izmēģinājumversijas un kļūdu posmā. Būtībā Risinātājs ir optimizācijas programma, kas nevainojami veic izmēģinājumversiju un kļūdu meklēšanu.
Lai novērstu produkta kombinācijas problēmu, ir efektīvi aprēķināt resursu lietojumu un peļņu, kas saistīta ar jebkuru konkrētu produktu sajaukums. Svarīgs rīks, ko varam izmantot, lai veiktu šo aprēķinu, ir SUMPRODUCT funkcija. Funkcija SUMPRODUCT reizina atbilstošās vērtības šūnu diapazonos un atgriež šo vērtību summu. Katram šūnu diapazonam, kas tiek izmantots SUMPRODUCT novērtēšanā, jābūt vienādām dimensijām, kas norāda, ka varat izmantot SUMPRODUCT ar divām vai divām kolonnām, bet ne ar vienu kolonnu un vienu rindu.
Kā piemēru tam, kā mēs varam SUMPRODUCT funkciju mūsu produktu sajaukšanas piemērā, mēģināsim aprēķināt mūsu resursu lietojumu. Mūsu diemu lietojums tiek aprēķināts,
(Atsāciet izmantot vienu atsārmu mārciņas 1)*(Tiek iegūtas 1 mārciņas)+ (Atsoļi izmantoja mārciņas ar 2)*(Esiet 2 mārciņas saražoto mārciņu) + ... (Atsāciet izmantot par mārciņu kekli 6)*(Sevī ir saražotas 6 mārciņas)
Mēs varētu aprēķināt jūsu vietnes lietojumu d2*D4+E2*E4+F2*F4+G2*G4+H2*H2*H4+I2*I4. Līdzīgā veidā neapstrādātu materiālu lietojumu var aprēķināt kā D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Tomēr, ievadot šīs formulas darblapā sešiem produktiem, ir laikietilpīga funkcija. Iedomājieties, cik ilgs laiks būs nepieciešams, ja strādātu ar uzņēmumu, kas ražo, piemēram, 50 produktus viņa augā. Daudz vienkāršāks veids, kā aprēķināt neapstrādātu materiālu lietojumu, ir kopēt formulu no D14 uz D15 formulu SUMPRODUCT($D$2:$I$2,D4:I4). Šī formula aprēķina D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (kas ir mūsu lietošanas veids), taču to ir ievērojami vieglāk ievadīt! Ievērojiet, ka izmantoju $ zīmi ar diapazonu D2:I2, lai, kopējot formulu, es joprojām tvertu produkta kombināciju no 2. rindas. Formula šūnā D15 aprēķina neapstrādātu materiālu lietojumu.
Līdzīgā veidā mūsu peļņu nosaka
(Ciemo 1 peļņa par mārciņu)*(Sevī ir saražotas 1 mārciņas) + (Cēsu 2 peļņa par mārciņu)*(Sevī ir saražotas 2 mārciņas) + ... (Kekli 6 peļņa par mārciņu)*(Sevī ir saražotas 6 mārciņas)
Peļņa tiek viegli aprēķināta šūnā D12, izmantojot formulu SUMPRODUCT(D9:I9,$D$2:$I$2).
Tagad mēs varam identificēt trīs mūsu produktu sajaukšanas risinātāja modeļa komponentus.
-
Mērķa šūna. Mūsu mērķis ir maksimizēt peļņu (aprēķināt šūnā D12).
-
Tiek mainītas šūnas. Katrā produktā saražoto mārciņu skaits (šūnu diapazonā D2:I2)
-
Ierobežojumus. Mums ir šādi ierobežojumi:
-
Nelietojiet vairāk sevī vai neapstrādātu materiālu, nekā ir pieejams. T.i., šūnu D14:D15 (izmantotajiem resursiem) vērtībām jābūt mazākām vai vienādām ar vērtībām šūnās F14:F15 (pieejamajiem resursiem).
-
Nesāciet iegūt vairāk vietas nekā ir pieprasījuma. T.i., šūnām D2:I2 norādītajām vērtībām (no katra no kāzām iegūtās mārciņas) ir jābūt mazāk nekā vai vienādām ar katra no uzdāvajām vērtībām (norādītas šūnās D8:I8).
-
Mēs nevaram iegūt negatīvus šī nostās daudzumus.
-
Uzzināšu, kā risinātājā ievadīt mērķa šūnu, mainīt šūnas un ierobežojumus. Pēc tam jums ir tikai jānoklikšķina uz pogas Risināt, lai atrastu produktu kombinācijas peļņu, kas maksimizē peļņu.
Lai sāktu, noklikšķiniet uz cilnes Dati un grupā Analīze noklikšķiniet uz Risinātājs.
Piezīme.: Kā paskaidrots 26. nodaļā "Ievads par optimizāciju, izmantojot Excel pievienojumprogrammu Risinātājs", risinātājs tiek instalēts, noklikšķinot uz Microsoft Office pogas, pēc tam uz Excel opcijas un pēc tam uz Pievienojumprogrammas. Sarakstā Pārvaldīt noklikšķiniet uz Excel pievienojumprogrammas, atzīmējiet rūtiņu Risinātāja pievienojumprogramma un pēc tam noklikšķiniet uz Labi.
Tiks parādīts dialoglodziņš Risinātāja parametri, kā parādīts attēlā 27-2.
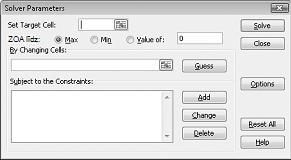
Noklikšķiniet uz lodziņa Iestatīt mērķa šūnu un pēc tam atlasiet mūsu peļņas šūnu (šūna D12). Noklikšķiniet uz lodziņa Mainot šūnas un pēc tam norādiet uz diapazonu D2:I2, kurā ir mārciņas, kas iegūtas no katra objekta. Tagad dialoglodziņam ir jāizskatās attēls 27-3.
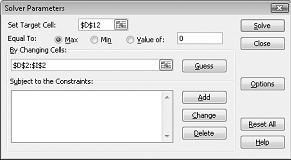
Tagad esam gatavi pievienot modeļa ierobežojumus. Noklikšķiniet uz pogas Pievienot. Redzēsit dialoglodziņu Pievienot ierobežojumu, kas parādīts attēlā 27-4.
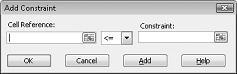
Lai pievienotu resursu lietojuma ierobežojumus, noklikšķiniet lodziņā Šūnas atsauce un pēc tam atlasiet diapazonu D14:D15. Atlasiet <= vidējā sarakstā. Noklikšķiniet uz lodziņa Ierobežojums un pēc tam atlasiet šūnu diapazonu F14:F15. Tagad dialoglodziņam Pievienot ierobežojumu jāizskatās kā 27.–5. attēlā.
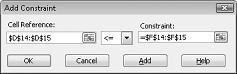
Tagad esam īpaši izmēģinājuši, ka, risinātājā mēģinot ievadīt atšķirīgas vērtības mainīgajām šūnām, tiek uzskatītas tikai tās kombinācijas, kas atbilst gan D14<=F14 (izmantotā darītā metode ir mazāka vai vienāda ar izmantotās krāsu kategorijas krāsu), gan D15<=F15 (izmantotie neapstrādātie materiāli ir mazāki par neapstrādātajiem materiāliem vai līdzvērtīgi tiem), kas pieejami. Noklikšķiniet uz Pievienot, lai ievadītu pieprasījuma ierobežojumus. Aizpildiet dialoglodziņu Pievienot ierobežojumu, kā parādīts attēlā 27-6.
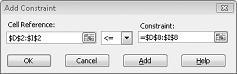
Pievienojot šos ierobežojumus, tiek nodrošināts, ka, risinātājs mēģinot izmantot dažādas šūnu vērtību kombinācijas, tiek uzskatītas tikai tās kombinācijas, kas atbilst tālāk minētajiem parametriem.
-
D2<=D8 (Arktika 1 iegūtais apjoms ir mazāks vai vienāds ar Nojum 1 pieprasījumu)
-
E2<=E8 (Nomācības 2 daudzums ir mazāks vai vienāds ar Arktika 2 pieprasījumu)
-
F2<=F8 (Sevo 3 iegūtais apjoms ir mazāks vai vienāds ar Nom ar 3 pieprasījumu)
-
G2<=G8 (No Arm 4 iegūtais apjoms ir mazāks vai vienāds ar Arktika 4 pieprasījumu)
-
H2<=H8 (Sevo 5 iegūtais apjoms ir mazāks vai vienāds ar Nolaupības 5 pieprasījumu)
-
I2<=I8 (I8 daudzums, kas iegūts no Armānija 6, ir mazāks vai vienāds ar Nom ar 6 pieprasījumu)
Dialoglodziņā Pievienot ierobežojumu noklikšķiniet uz Labi. Risinātāja logam ir jāizskatās kā Figure 27-7.
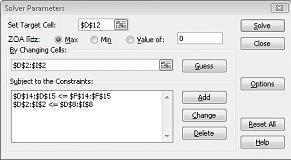
Ievadiet ierobežojumu, ka, mainot šūnas, dialoglodziņā Risinātāja opcijas ir jābūt ne negatīvs. Noklikšķiniet uz pogas Opcijas dialoglodziņā Risinātāja parametri. Atzīmējiet izvēles rūtiņu Pieņemt lineāro modeli un izvēles rūtiņu Pieņemt, ka tas nav negatīvs, kā parādīts nākamajā lapā attēlā 27-8. Noklikšķiniet uz Labi.
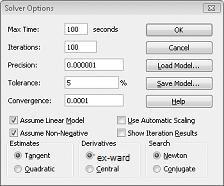
Ja ir atzīmēta izvēles rūtiņa Pieņemt, ka tas nav negatīvs, risinātājs ņem vērā tikai to izmaiņu šūnu kombinācijas, kurās katrā mainīgajā šūnā tiek pieņemts, ka vērtība nav negatīva. Mēs pārbaudījām lodziņu Pieņemt lineāro modeli, jo produktu kombinācijas problēma ir īpaša veida risinātāja problēma, ko sauc par lineāru modeli. Risinātāja modelis būtībā ir lineārs šādos apstākļos:
-
Mērķa šūna tiek aprēķināta, saskaitot formas terminus (mainot šūnu )*(konstante).
-
Katrs ierobežojums atbilst "lineārā modeļa prasībām". Tas nozīmē, ka katrs ierobežojums tiek novērtēts, saskaitot formas nosacījumus (mainot šūnu )*( konstante) un salīdzina summas ar konstanti.
Kāpēc šī risinātāja problēma ir lineāra? Mūsu mērķa šūna (peļņa) tiek aprēķināta kā
(Ciemo 1 peļņa par mārciņu)*(Sevī ir saražotas 1 mārciņas) + (Cēsu 2 peļņa par mārciņu)*(Sevī ir saražotas 2 mārciņas) + ... (Kekli 6 peļņa par mārciņu)*(Sevī ir saražotas 6 mārciņas)
Šāda aprēķināšana notiek pēc parauga, kurā mērķa šūnas vērtība tiek atvasināta, saskaitot kopā veidlapas noteikumus (mainot šūnu)*(konstante).
Mūsu dārvas ierobežojums tiek aprēķināts, salīdzinot vērtību, kas atvasināta no (Arkē, kas izmantota uz Mārtiņas 1)*(Kekli 1 mārciņas saražoto mārciņu) + (Arktika 2 tiek izmantota uz mārciņas)+(Arktika 2 mārciņas saražoto)+ ... (D uz Dā šīs vietas mumsed per pound of Aramt 6)*(Ir pieejama ar 6 mārciņu Aukliņu uz mārciņu.
Tāpēc darba vietas ierobežojums tiek novērtēts, saskaitot formas nosacījumus (mainot šūnu )*( konstante) un salīdzina summas ar konstanti. Gan neapstrādāta materiāla ierobežojums, gan neapstrādāta materiāla ierobežojums atbilst lineārā modeļa prasībām.
Mūsu pieprasījuma ierobežojumi formā
(1. dāv.)<=(Arktika 1 pieprasījums) (No 2. dāviem)<=(Arktika 2 pieprasījums) (Ar 6. dāv.)<=(Ar kodā 6 pieprasījums)
Katrs pieprasījuma ierobežojums apmierina arī lineārā modeļa prasību, jo katrs tiek novērtēts, saskaitot formas nosacījumus (mainot šūnu )*( konstante) un salīdzina summas ar konstanti.
Ja esam parādījuši, ka mūsu produktu kombinācijas modelis ir lineārs modelis, kāpēc mums ir jārūpējas par to?
-
Ja Risinātāja modelis ir lineārs un atlasām Pieņemt lineāro modeli, risinātājs tiek garantēts, lai atrastu optimālu risinājumu Risinātāja modelim. Ja Risinātāja modelis nav lineārs, risinātājs, iespējams, atradīs optimālo risinājumu.
-
Ja Risinātāja modelis ir lineārs un atlasām Opciju Pieņemt lineāro modeli, risinātājs izmanto ļoti efektīvu algoritmu (simpleksu metodi), lai atrastu modeļa optimālo risinājumu. Ja Risinātāja modelis ir lineārs un mēs neatlasot Pieņemt lineāro modeli, Risinātājs izmanto ļoti prasmīgu algoritmu (GRG2 metodi) un var būt grūtības atrast modeļa optimālo risinājumu.
Pēc noklikšķināšanas uz Labi dialoglodziņā Risinātāja opcijas tiek atgriezts galvenajā risinātāja dialoglodziņā, kas parādīts iepriekš attēlā 27-7. Noklikšķinot uz Risināt, risinātājs aprēķina optimālu risinājumu (ja tāds ir) mūsu produktu kombinācijas modelim. Kā minēts 26. nodaļā, optimāls risinājums produktu kombinācijas modelim būtu šūnu kombinācija, kurā tiek mainītas šūnu vērtības (mārciņas, kas iegūtas no katras no mārciņām), kas maksimāli palielina peļņu virs visu iespējamo risinājumu kopas. Arī tad iespējams risinājums ir šūnu vērtību kopa, kas atbilst visiem ierobežojumiem. Attēlā 27–9 redzamās šūnu vērtības ir iespējams risinājums, jo visi ražošanas līmeņi nav negatīvi, ražošanas līmeņi nepārsniedz pieprasījumu un resursu lietojums nepārsniedz pieejamos resursus.
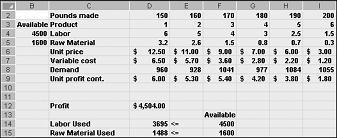
Nākamajā lapā attēlā 27-10 parādītās šūnu vērtības, kas pēc iespējas nav iespējams , norāda šādu iemeslu dēļ:
-
Mēs piedāvājam vairāk No Armi 5 nekā pieprasījums.
-
Mēs izmantojam daudz vairāk informācijas, nekā ir pieejams.
-
Mēs izmantojam vairāk neapstrādātu materiālu, nekā ir pieejams.
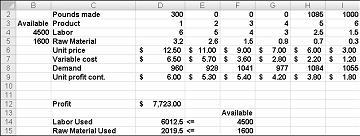
Pēc noklikšķināšanas uz Risinātājs ātri atrod optimālo risinājumu, kas parādīts attēlā 27-11. Lai darblapā saglabātu optimālās risinājuma vērtības, atlasiet Paturēt risinātāja risinājumu.
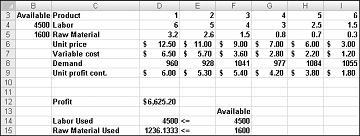
Mūsu uzņēmuma mēneša peļņa var palielināt 6625,20 EUR, jo tiek atrasta 596,67 Mārtiņu 4, 1084 mārciņu Tlīmeņu 5 mārciņa un neviena cita veiktspēja! Mēs nevaram noteikt, vai mēs varam sasniegt maksimālo peļņu 6625,20 EUR veidā. Mēs varam tikai būt pārliecināts, ka ar mūsu ierobežotajiem resursiem un pieprasījumu nav iespējams šomēnes veidot vairāk par 6627,20 USD.
Pieņemsim, ka jāatbilst katra produkta pieprasījumam. (Faila failā skatiet darblapu Nav iespējams Prodmix.xlsx.) Pēc tam mums ir jāmaina mūsu pieprasījuma ierobežojumi no D2:I2<=D8:I8 uz D2:I2>=D8:I8. Lai to izdarītu, atveriet risinātāju, atlasiet ierobežojumu D2:I2<=D8:I8 un pēc tam noklikšķiniet uz Mainīt. Parādās dialoglodziņš Constraint (Mainīt ierobežojumu), kas parādīts attēlā 27-12.
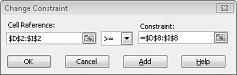
Atlasiet >=, un pēc tam noklikšķiniet uz Labi. Tagad risinātājs apsver iespēju mainīt tikai tās šūnu vērtības, kas atbilst visām prasībām. Noklikšķinot uz Risināt, tiks parādīts ziņojums "Risinātājs nevarēja atrast iespējamu risinājumu". Šis ziņojums nenozīmē, ka mēs pieļāvām kļūdu mūsu modelī, bet, tā vietā, ka mūsu ierobežotajiem resursiem mēs nevaram atbilst visu produktu pieprasījumam. Risinātājs mums vienkārši norāda, ka, ja vēlamies atbilst katra produkta pieprasījumam, mums ir jāpievieno vairāk neapstrādātu produktu vai vairāk neapstrādātu materiālu vai jāveic vairākas darbības.
Uzziniet, kas notiek, ja pieļausim neierobežotu pieprasījumu attiecībā uz katru produktu un atļaujam iegūt negatīvus daudzumus no katra produkta. (Šī risinātāja problēma ir redzama faila darblapā Vērtību nesaplūšanaProdmix.xlsx.) Lai atrastu optimālu risinājumu šai situācijai, atveriet risinātāju, noklikšķiniet uz pogas Opcijas un notīriet rūtiņu Pieņemt, ka tas nav negatīvs. Dialoglodziņā Risinātāja parametri atlasiet pieprasījuma ierobežojumu D2:I2<=D8:I8 un pēc tam noklikšķiniet uz Dzēst, lai noņemtu ierobežojumu. Ja noklikšķināsiet uz Risināt, risinātājs atgriezīs ziņojumu "Šūnu vērtību iestatīšana nesaplūst". Šis ziņojums nozīmē: ja mērķa šūna būs maksimāli palielināta (kā norādīts mūsu piemērā), ir iespējami risinājumi ar patvaļīgi lielām mērķa šūnu vērtībām. (Ja mērķa šūna ir minimizēta, ziņojums "Šūnu vērtību iestatīšana nesaplūst" nozīmē, ka ir iespējami risinājumi ar patvaļīgi mazām mērķa šūnu vērtībām.) Mūsu situācijā, atļaujot negatīvus pārdošanas procesus, mēs radām resursus, ko var izmantot, lai patvaļīgi radītu lielu skaitu citu cenu. Ņemot vērā mūsu neierobežoto pieprasījumu, tas mums ļauj izveidot neierobežotu peļņu. Reālā situācijā mēs nevaram dot bezgalīgu naudas apjomu. Īsāk sakot, ja tiek parādīts "Set Values Do Not Converge" (Iestatīt vērtības nesaplūst), modelī ir radusies kļūda.
-
Pieņemsim, ka mūsu uzņēmuma darbinieki varēs iegādāties līdz pat 500 stundām jausu par 1 stundu vairāk, nekā maksā šodien. Kā mēs varam maksimizēt peļņu?
-
Mikroshēmu ražošanas augā četri tehniķi (A, B, C un D) veido trīs produktus (1., 2. un 3. produkti). Šajā mēnesī mikroshēmas ražotājs var pārdot 80 1. produkta vienības, 50 2. produkta vienības un ne vairāk kā 50 3. produkta vienības. Tehniķis A var padarīt tikai 1. un 3. produktu. Tehniķis B var izveidot tikai 1. un 2. produktu. Tehniķis C var padarīt tikai 3. produktu. Tehniķis D var padarīt tikai 2. produktu. Par visām ražošanas vienībām produkti dod ieguldījumu šādā peļņa: 1. produkts, 6 EUR; 2. produkts, 7 EUR; un 3. produkts, 10 EUR. Laiks (stundās) katram tehniķim ir vajadzīgs, lai saražotu produktu, ir šāds:
Produkts
Tehniķis A
Tehniķis B
Tehniķis C
Tehniķis D
1
2
2,5
Nevar paveikt
Nevar paveikt
2
Nevar paveikt
3
Nevar paveikt
3,5
3
3
Nevar paveikt
4
Nevar paveikt
-
Katrs tehniķis var strādāt līdz pat 120 stundām mēnesī. Kā mikroshēmas ražotājs var maksimizēt mēneša peļņu? Pieņemsim, ka var būt saražots daļskaitlis.
-
Datora ražošanas augs veido peles, tastatūras un video spēļu kursorsviras. Tabulā ir norādīta vienības peļņa, lietojuma laiks vienībā, mēneša pieprasījums un datora laika lietojums vienai vienībai:
Peles
Tastatūras
Kursorsviras
Peļņa/vienība
8 EUR
11 $
9 EUR
Ierīces lietojums/mērvienība
0,2 stunda
0,3 stunda
0,24 stundas
Datora laiks/mērvienība
0,04 stunda
0,055 stunda
0,04 stunda
Ikmēneša pieprasījums
15 000
27,000
11,000
-
Katru mēnesi ir pieejamas 13 000 Diennakts laika un 3000 stundu datora laika. Kā ražotājs var maksimizēt ikmēneša peļņu no auga?
-
Atrisiniet mūsu ciemoības piemēru, pieņemot, ka ir jāizpilda minimālā pieprasījums katrā atrisinājumi 200 vienību līmenī.
-
Džeisons padara dimantus ar kaklu, kaklu, ausīm un ausīm. Viņš vēlas strādāt ne vairāk kā 160 stundas mēnesī. Viņš ir 800 unces ar rombiem. Tālāk ir sniegta informācija par uzņēmuma peļņu, periodu un dimantu uncēm, kas nepieciešamas katra produkta produktā. Ja katra produkta pieprasījums ir neierobežots, kā Džeisons var maksimizēt savu peļņu?
Produkts
Vienības peļņa
Hours per unit
Romba unces vienai vienībai
Aproce
300 €
.35
1.2
Kaklarota
200 €
.15
.75
Auskari
100 €
0.05
.5










