Viktig!: Støtte for Office 2016 og Office 2019 opphørte 14. oktober 2025. Oppgrader til Microsoft 365 for å arbeide hvor som helst fra en hvilken som helst enhet, og fortsett å motta støtte. Skaff deg Microsoft 365
Denne artikkelen beskriver hvordan du bruker Problemløser, et tilleggsprogram for Microsoft Excel som du kan bruke til hva-skjer-hvis-analyse, for å finne en optimal produktblanding.
Hvordan kan jeg fastslå den månedlige produktblandingen som maksimerer lønnsomheten?
Firmaer må ofte bestemme antallet for hvert produkt som skal produseres på månedlig basis. I sin enkleste form innebærer produktblandingsproblemet hvordan du fastslår mengden av hvert produkt som skal produseres i løpet av en måned for å maksimere fortjenesten. Produktblandingen må vanligvis følge følgende begrensninger:
-
Produktblanding kan ikke bruke flere ressurser enn det som er tilgjengelig.
-
Det er begrenset etterspørsel etter hvert produkt. Vi kan ikke produsere mer av et produkt i løpet av en måned enn etterspørselen tilsier, fordi den overflødige produksjonen er bortkastet (for eksempel et forgjengelig stoff).
La oss nå løse følgende eksempel på produktblandingsproblemet. Du finner løsningen på dette problemet i filen Prodmix.xlsx, som vist i figur 27-1.
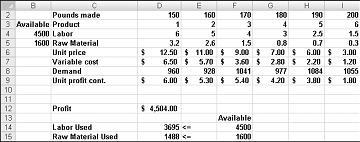
La oss si at vi jobber for et legemiddelselskap som produserer seks forskjellige produkter på anlegget. Produksjon av hvert produkt krever arbeid og råmateriale. Rad 4 i figur 27-1 viser arbeidstimene som trengs for å produsere et pund av hvert produkt, og rad 5 viser pund råmateriale som trengs for å produsere et pund av hvert produkt. For eksempel krever produksjon av et pund produkt 1 seks timer arbeid og 3,2 pounds råmateriale. For hvert stoff gis prisen per pund i rad 6, enhetskostnaden per pund gis i rad 7, og resultatbidraget per pund gis i rad 9. For eksempel selger Produkt 2 for $ 11,00 per pund, pådrar seg en enhetskostnad på $ 5,70 per pund, og bidrar med $ 5,30 fortjeneste per pund. Månedens etterspørsel etter hvert stoff er gitt i rad 8. Etterspørselen etter produkt 3 er for eksempel 1041 pund. Denne måneden, 4500 timer med arbeidskraft og 1600 pounds av råmateriale er tilgjengelig. Hvordan kan dette selskapet maksimere sin månedlige fortjeneste?
Hvis vi ikke visste noe om Excel Solver, ville vi angripe dette problemet ved å konstruere et regneark for å spore fortjeneste og ressursbruk knyttet til produktblandingen. Deretter vil vi bruke prøveversjon og feiling til å variere produktblandingen for å optimalisere fortjenesten uten å bruke mer arbeidskraft eller råmateriale enn det som er tilgjengelig, og uten å produsere noe stoff i overkant av etterspørselen. Vi bruker Problemløser i denne prosessen bare på prøve-og-feil-fasen. Problemløser er i hovedsak en optimaliseringsmotor som feilfritt utfører prøve-og-feil-søket.
En nøkkel til å løse problemet med produktblandingen er effektivt å beregne ressursbruken og fortjenesten som er knyttet til en gitt produktblanding. Et viktig verktøy som vi kan bruke til å lage denne beregningen, er SUMMERPRODUKT funksjonen. Funksjonen SUMMERPRODUKT multipliserer tilsvarende verdier i celleområder og returnerer summen av disse verdiene. Hvert celleområde som brukes i en SUMMERPRODUKT evaluering, må ha samme dimensjoner, noe som betyr at du kan bruke SUMMERPRODUKT med to rader eller to kolonner, men ikke med én kolonne og én rad.
Som et eksempel på hvordan vi kan bruke SUMMERPRODUKT-funksjonen i eksemplet på produktmiks, kan vi prøve å beregne ressursbruken vår. Arbeidsbruken beregnes av
(Arbeiderpartiet brukt per pund av narkotika 1)*(Narkotika 1 pounds produsert)+ (Arbeiderpartiet brukt per pund av narkotika 2)*(Narkotika 2 pounds produsert) + ... (Arbeiderpartiet brukt per pund av narkotika 6)*(Narkotika 6 pounds produsert)
Vi kunne beregne arbeidsbruk på en mer kjedelig måte som D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. På samme måte kan råmaterialebruk beregnes som D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Det er imidlertid tidkrevende å skrive inn disse formlene i et regneark for seks produkter. Tenk deg hvor lang tid det ville ta hvis du jobbet med et selskap som produserte, for eksempel 50 produkter på anlegget. En mye enklere måte å beregne arbeid og råstoffbruk på, er å kopiere formelen SUMMERPRODUKT ($D$2:$I$2,D4:I4) fra D14 til D15. Denne formelen beregner D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (som er arbeidsbruken vår), men det er mye enklere å angi! Legg merke til at jeg bruker $-tegnet med området D2:I2, slik at når jeg kopierer formelen, registrerer jeg fortsatt produktblandingen fra rad 2. Formelen i celle D15 beregner bruk av råmaterialer.
På lignende måte bestemmes fortjenesten vår av
(Narkotika 1 fortjeneste per pund)*(Narkotika 1 pounds produsert) + (Drug 2 fortjeneste per pund)*(Drug 2 pounds produsert) + ... (Narkotika 6 fortjeneste per pund)*(Narkotika 6 pounds produsert)
Fortjeneste beregnes enkelt i celle D12 med formelen SUMMERPRODUKT(D9:I9,$D$2:$I$2).
Vi kan nå identifisere de tre komponentene i problemløsermodellen vår for produktmiksen.
-
Målcelle. Målet vårt er å maksimere fortjenesten (beregnet i celle D12).
-
Endre celler. Antall pund som produseres av hvert produkt (oppført i celleområdet D2:I2)
-
Begrensninger. Vi har følgende begrensninger:
-
Ikke bruk mer arbeid eller råmateriale enn det som er tilgjengelig. Det vil si at verdiene i cellene D14:D15 (ressursene som brukes) må være mindre enn eller lik verdiene i cellene F14:F15 (de tilgjengelige ressursene).
-
Ikke produsere mer av et stoff enn det som er etterspurt. Det vil si at verdiene i cellene D2:I2 (pund produsert av hvert legemiddel) må være mindre enn eller lik etterspørselen etter hvert stoff (oppført i celle D8:I8).
-
Vi kan ikke produsere en negativ mengde av noe stoff.
-
Jeg skal vise deg hvordan du skriver inn målcellen, endrer celler og begrensninger i Problemløser. Alt du trenger å gjøre, er å klikke Løs-knappen for å finne en produktblanding som maksimeres for profitt!
Klikk fanen Data for å begynne, og klikk Problemløser i Analyse-gruppen.
Obs!: Som forklart i kapittel 26: «En innføring i optimalisering med Excel Problemløser», installeres Problemløser ved å klikke Microsoft Office-knappen og deretter Alternativer for Excel, etterfulgt av tillegg. Klikk Excel-tillegg i Behandle-listen, merk av for Problemløsertillegg, og klikk deretter OK.
Dialogboksen Problemløserparametere vises, som vist i figur 27-2.
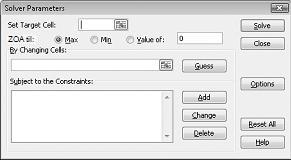
Klikk boksen Angi målcelle, og velg deretter fortjenestecellen (celle D12). Klikk boksen Ved å endre celler, og pek deretter på området D2:I2, som inneholder pundene som produseres av hvert legemiddel. Dialogboksen skal nå se figur 27-3.
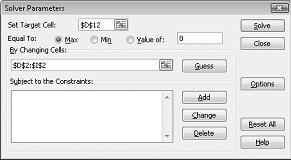
Vi er nå klare til å legge til begrensninger i modellen. Klikk Legg til-knappen. Dialogboksen Legg til betingelse vises i figur 27-4.
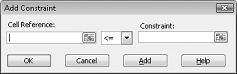
Hvis du vil legge til begrensninger for ressursbruk, klikker du cellereferanseboksen og merker deretter området D14:D15. Velg <= fra den midterste listen. Klikk Betingelse-boksen, og merk deretter celleområdet F14:F15. Dialogboksen Legg til betingelse skal nå se ut som figur 27–5.
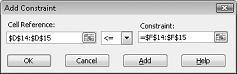
Vi har nå sikret at når Problemløser prøver forskjellige verdier for de endrede cellene, vil bare kombinasjoner som tilfredsstiller både D14<=F14 (arbeid som brukes er mindre enn eller lik arbeid tilgjengelig) og D15<=F15 (råstoff som brukes er mindre enn eller lik råmateriale tilgjengelig) vurderes. Klikk Legg til for å angi behovsbetingelsene. Fyll ut dialogboksen Legg til betingelse, som vist i Figur 27-6.
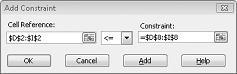
Hvis du legger til disse begrensningene, sikrer du at når Problemløser prøver forskjellige kombinasjoner for de endrede celleverdiene, vurderes bare kombinasjoner som oppfyller følgende parametere:
-
D2<=D8 (mengden produsert av legemiddel 1 er mindre enn eller lik etterspørselen etter legemiddel 1)
-
E2<=E8 (mengden produsert av legemiddel 2 er mindre enn eller lik etterspørselen etter legemiddel 2)
-
F2<=F8 (mengden produsert av legemiddel 3 er mindre enn eller lik etterspørselen etter legemiddel 3)
-
G2<=G8 (mengden produsert av legemiddel 4 er mindre enn eller lik etterspørselen etter legemiddel 4)
-
H2<=H8 (mengden produsert av legemiddel 5 er mindre enn eller lik etterspørselen etter legemiddel 5)
-
I2<=I8 (mengden produsert av Narkotika 6 laget er mindre enn eller lik etterspørselen etter Narkotika 6)
Klikk OK i dialogboksen Legg til betingelse. Problemløser-vinduet skal se ut som figur 27-7.
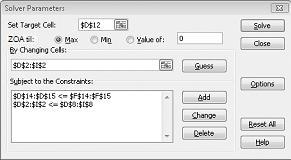
Vi angir betingelsen om at endring av celler må være ikke-negativ i dialogboksen Alternativer for problemløser. Klikk Alternativer-knappen i dialogboksen Problemløserparametere. Merk av for Anta lineær modell og Anta ikke-negativ, som vist i figur 27-8 på neste side. Klikk OK.
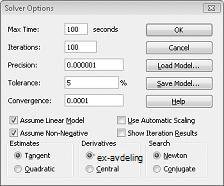
Hvis du merker av for Anta ikke-negativ, sikrer du at Problemløser bare vurderer kombinasjoner av endringsceller der hver endringscelle forutsetter en ikke-negativ verdi. Vi merket av for Anta lineær modell fordi problemet med produktblandingen er en spesiell type problemløser som kalles en lineær modell. En problemløsermodell er lineær under følgende betingelser:
-
Målcellen beregnes ved å legge sammen vilkårene i skjemaet (endre celle)*(konstant).
-
Hver betingelse tilfredsstiller «lineært modellkrav». Dette betyr at hver betingelse evalueres ved å legge sammen vilkårene i skjemaet (endre celle)*(konstant) og sammenligne summene med en konstant.
Hvorfor er problemlinjediagram for problemløseren lineær? Vår målcelle (fortjeneste) beregnes som
(Narkotika 1 fortjeneste per pund)*(Narkotika 1 pounds produsert) + (Drug 2 fortjeneste per pund)*(Drug 2 pounds produsert) + ... (Narkotika 6 fortjeneste per pund)*(Narkotika 6 pounds produsert)
Denne beregningen følger et mønster der målcellens verdi er avledet ved å legge sammen termer i skjemaet (endre celle)*(konstant).
Vår arbeidsbetingelse evalueres ved å sammenligne verdien avledet fra (Labor brukt per pund av Narkotika 1)*(Drug 1 pounds produsert) + (Labor brukes per pund av Drug 2)*(Drug 2 pounds produsert)+ ... (Arbeiderpartiet ossed per pund av Narkotika 6)*(Drug 6 pounds produsert) til arbeidskraft tilgjengelig.
Derfor evalueres arbeidsbetingelsen ved å legge sammen vilkårene i skjemaet (endre celle)*(konstant) og sammenligne summene med en konstant. Både arbeidsbetingelsen og råmaterialebetingelsen oppfyller det lineære modellkravet.
Våre behovsbegrensninger tar skjemaet
(Legemiddel 1 produsert)<=(Etterspørsel etter legemiddel 1) (Legemiddel 2 produsert)<=(Etterspørsel etter legemiddel 2) §(Legemiddel 6 produsert)<=(Etterspørsel etter legemiddel 6)
Hver behovsbetingelse tilfredsstiller også det lineære modellkravet, fordi hver av dem evalueres ved å legge sammen vilkårene i skjemaet (endre celle)*(konstant) og sammenligne summene med en konstant.
Etter å ha vist at produktblandingsmodellen vår er en lineær modell, hvorfor skal vi bry oss?
-
Hvis en problemløsermodell er lineær og vi velger Anta lineær modell, er Problemløser garantert å finne den optimale løsningen på Problemløser-modellen. Hvis en problemløsermodell ikke er lineær, kan det hende problemløseren ikke finner den optimale løsningen.
-
Hvis en problemløsermodell er lineær og vi velger Anta lineær modell, bruker Problemløser en svært effektiv algoritme (simplex-metoden) for å finne modellens optimale løsning. Hvis en problemløsermodell er lineær og vi ikke velger Anta lineær modell, bruker Problemløser en svært ineffektiv algoritme (GRG2-metoden) og kan ha problemer med å finne modellens optimale løsning.
Når du har klikket OK i dialogboksen Alternativer for problemløser, går vi tilbake til hoveddialogboksen for Problemløser, som vises tidligere i figur 27-7. Når vi klikker Løs, beregner Problemløser en optimal løsning (hvis det finnes en) for produktmiksmodellen vår. Som jeg sa i kapittel 26, ville en optimal løsning på produktblandingsmodellen være et sett med endrede celleverdier (pund produsert av hvert stoff) som maksimerer fortjenesten over settet med alle mulige løsninger. En mulig løsning er igjen et sett med endring av celleverdier som tilfredsstiller alle begrensninger. De endrede celleverdiene som vises i figur 27-9, er en mulig løsning fordi alle produksjonsnivåer er ikke-negative, produksjonsnivåer overskrider ikke etterspørselen, og ressursbruken overskrider ikke tilgjengelige ressurser.
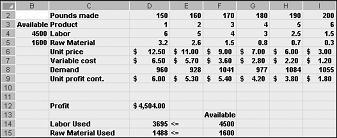
De endrede celleverdiene som vises i figur 27-10 på neste side, representerer en umulig løsning av følgende årsaker:
-
Vi produserer mer av Drug 5 enn etterspørselen etter det.
-
Vi bruker mer arbeid enn det som er tilgjengelig.
-
Vi bruker mer råmateriale enn det som er tilgjengelig.
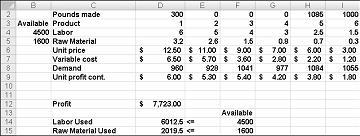
Når du har klikket Løs, finner Problemløser raskt den optimale løsningen som vises i figur 27-11. Du må velge Behold problemløserløsning for å bevare de optimale løsningsverdiene i regnearket.
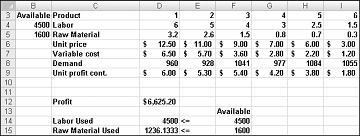
Vår narkotika selskapet kan maksimere sin månedlige fortjeneste på et nivå på $ 6,625.20 ved å produsere 596.67 pounds av Drug 4, 1084 pounds av Drug 5, og ingen av de andre stoffene! Vi kan ikke avgjøre om vi kan oppnå maksimal fortjeneste på $ 6625,20 på andre måter. Alt vi kan være sikre på er at med våre begrensede ressurser og etterspørsel, er det ingen måte å gjøre mer enn $ 6,627.20 denne måneden.
La oss si at etterspørselen etter hvert produkt må oppfylles. (Se regnearket Ingen mulig løsning i filen Prodmix.xlsx.) Vi må deretter endre behovsbegrensningene fra D2:I2<=D8:I8 til D2:I2>=D8:I8. Dette gjør du ved å åpne Problemløser, velge D2:I2-<=D8:I8-begrensningen, og deretter klikke Endre. Dialogboksen Endre betingelse, som vises i figur 27-12, vises.
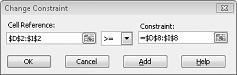
Velg >=, og klikk deretter OK. Vi har nå sikret at Problemløser vil vurdere å endre bare celleverdier som oppfyller alle krav. Når du klikker Løs, ser du meldingen Problemløser finner ikke en mulig løsning. Denne meldingen betyr ikke at vi har gjort en feil i modellen vår, men heller at med våre begrensede ressurser, kan vi ikke møte etterspørselen etter alle produkter. Problemløser forteller oss ganske enkelt at hvis vi ønsker å møte etterspørselen etter hvert produkt, må vi legge til mer arbeidskraft, flere råvarer eller mer av begge deler.
La oss se hva som skjer hvis vi tillater ubegrenset etterspørsel etter hvert produkt, og vi tillater negative mengder som skal produseres av hvert stoff. (Du kan se problemet med problemløseren i regnearket Angi verdier som ikke konvergerer i filen Prodmix.xlsx.) Hvis du vil finne den optimale løsningen for denne situasjonen, åpner du Problemløser, klikker Alternativer-knappen og fjerner merket for Anta ikke-negativ. Velg behovsbetingelsen D2:I2<=D8:I8 i dialogboksen Problemløserparametere, og klikk deretter Slett for å fjerne betingelsen. Når du klikker Løs, returnerer Problemløser meldingen Angi celleverdier konvergerer ikke. Denne meldingen betyr at hvis målcellen skal maksimeres (som i vårt eksempel), finnes det mulige løsninger med vilkårlig store målcelleverdier. (Hvis målcellen skal minimeres, betyr meldingen Angi celleverdier ikke konvergerende at det finnes mulige løsninger med vilkårlig små målcelleverdier.) I vår situasjon, ved å tillate negativ produksjon av et stoff, vi i praksis "skape" ressurser som kan brukes til å produsere vilkårlig store mengder andre stoffer. Gitt vår ubegrensede etterspørsel, dette tillater oss å gjøre ubegrenset fortjeneste. I en reell situasjon kan vi ikke tjene en uendelig sum penger. Kort sagt, hvis du ser «Angi verdier ikke konvergerer», har modellen en feil.
-
La oss si at legemiddelselskapet vårt kan kjøpe opptil 500 arbeidstimer til kr 100 per time enn gjeldende lønnskostnader. Hvordan kan vi maksimere fortjenesten?
-
Ved en brikkefabrikk produserer fire teknikere (A, B, C og D) tre produkter (produkter 1, 2 og 3). Denne måneden kan brikkeprodusenten selge 80 enheter produkt 1, 50 enheter produkt 2 og maksimalt 50 enheter av produkt 3. Tekniker A kan bare lage produkter 1 og 3. Tekniker B kan bare lage produkter 1 og 2. Tekniker C kan bare lage Produkt 3. Tekniker D kan bare lage Produkt 2. For hver enhet som produseres, bidrar produktene med følgende fortjeneste: Produkt 1, USD 6, Produkt 2, $7; og Produkt 3, USD 10. Tiden (i timer) hver tekniker trenger for å produsere et produkt, er som følger:
Produkt
Tekniker A
Tekniker B
Tekniker C
Tekniker D
1
2
2,5
Kan ikke gjøre
Kan ikke gjøre
2
Kan ikke gjøre
3
Kan ikke gjøre
3,5
3
3
Kan ikke gjøre
4
Kan ikke gjøre
-
Hver tekniker kan arbeide opptil 120 timer per måned. Hvordan kan brikkeprodusenten maksimere sin månedlige fortjeneste? Anta at et brøkdelsantall kan produseres.
-
En dataproduksjonsanlegg produserer mus, tastaturer og videospill joysticks. Fortjenesten per enhet, arbeid per enhet, månedlig etterspørsel og maskintidsbruk per enhet gis i tabellen nedenfor:
Mus
Tastaturer
Styrespaker
Fortjeneste/enhet
KR 8
KR 11
KR 9
Arbeidsbruk/-enhet
0,2 time
0,3 timer
0,24 timer
Maskintid/-enhet
0,04 timer
0,055 time
0,04 timer
Månedlig etterspørsel
15 000
27,000
11,000
-
Hver måned er totalt 13 000 arbeidstimer og 3000 timer maskintid tilgjengelig. Hvordan kan produsenten maksimere sitt månedlige fortjenestebidrag fra anlegget?
-
Løs vårt narkotikaeksempel forutsatt at en minimumsetterspørsel på 200 enheter for hvert stoff må oppfylles.
-
Jason lager diamantarmbånd, halskjeder og øredobber. Han ønsker å jobbe maksimalt 160 timer per måned. Han har 800 gram diamanter. Overskuddet, arbeidstiden og gram diamanter som kreves for å produsere hvert produkt, gis nedenfor. Hvis etterspørselen etter hvert produkt er ubegrenset, hvordan kan Jason maksimere sin fortjeneste?
Produkt
Enhetsfortjeneste
Arbeidstimer per enhet
Gram diamanter per enhet
Armbånd
kr 300
.35
1.2
Halsbånd
kr 200
.15
.75
Øredobber
$100
,05
.5










