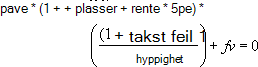NÅVERDI (funksjon)

Syntaks

NÅVERDI(rente;antall_innbet;innbet;sluttverdi;type)

Rente     er rentesatsen per periode. Hvis du for eksempel får et billån til en rentesats lik 10% pro anno og foretar månedlige innbetalinger, vil rentesatsen per måned være lik 10%/12 eller 0,83%. Du kan altså sette inn 10%/12, 0,83% eller 0,0083 for argumentet rente i formelen.

Antall_innbet     er det totale antallet betalingsperioder i en annuitet. Hvis du for eksempel tar opp et billån over fire år og foretar månedlige innbetalinger, består lånet ditt av 4*12 (eller 48) perioder. Du angir da 48 for argumentet antall_innbet i formelen.

Innbetaling     er betalingen som foretas hver periode, og kan ikke endres i løpet av annuitetens levetid. Normalt vil innbetaling omfatte hovedstol og renter, men ikke skatt, gebyrer eller avgifter. Hvis du for eksempel får et billån på kr 10.000 over fire år til 12% rente, vil de månedlige innbetalingene være kr 263,33. Du kan altså sette inn -263,33 for argumentet innbetaling i formelen. Hvis innbetaling utelates, må du inkludere argumentet sluttverdi.

Sluttverdi     er den fremtidige verdien, eller en kontantsaldo du vil oppnå etter at den siste innbetalingen er foretatt. Hvis argumentet sluttverdi er utelatt, blir det satt lik 0 (den fremtidige verdien av et lån er for eksempel lik 0). Hvis du for eksempel vil spare kr 50.000 for å kunne betale for et bestemt prosjekt om 18 år, er kr 50.000 den fremtidige verdien. Du kan deretter anslå en forsiktig rentesats og finne ut hvor mye du må spare hver måned. Hvis sluttverdi utelates, må du inkludere argumentet innbetaling.

Type     er tallet 0 eller 1 og angir når betalingen forfaller.

Merknader

• Pass på at du er konsekvent når det gjelder enhetene du bruker for å angi rente og antall_innbet. Hvis du foretar månedlige innbetalinger på et lån som løper over fire år med 12 % rente årlig, bruker du 12%/12 for rente og 4*12 for antall_innbet. Hvis du foretar innbetalingene en gang per år på det samme lånet, bruker du 12 % for rente og 4 for antall_innbet.

• Følgende funksjoner gjelder for annuiteter: FV; RAVDRAG; AVDRAG; AMORT; PV; og RENTE. En annuitet er en serie faste innbetalinger over en sammenhengende periode. Et billån eller et pantelån er eksempler på en annuitet. Hvis du vil ha mer informasjon om dette, se beskrivelsen av de enkelte annuitetsfunksjonene.

• For annuitetsfunksjonene blir penger du betaler ut, for eksempel innskudd på sparekonti, angitt med negative tall, og penger du får inn, som sjekker med utbytte, blir angitt med positive tall. Et innskudd på kr 1000 i en bank vil for eksempel representeres av argumentet -1000 hvis det er du som er innskyteren, og av argumentet 1000 hvis det er du som er banken.

• Ett økonomisk argument løses når det gjelder de andre. Hvis rente ikke er lik 0, er:

  

  Hvis rente er lik 0, er:

  (innbetaling * antall_innbet) + nåverdi + sluttverdi = 0

Eksempel

I eksemplet nedenfor:

• Avdrag er pengene som betales ut av en forsikringsannuitet på slutten av hver måned.

• Rente er rentesatsen som er opptjent på pengene som utbetales.

• Nper er årene pengene vil bli utbetalt.

Rentesatsen er dividert med 12 for å få en månedlig rentesats. Årene pengene utbetales multipliseres med 12 for å få antall innbetalinger.

Resultatet er negativt fordi det representerer penger som du betaler, en utgående kontantstrøm. Hvis du blir bedt om å betale (60.000) for livrente, vil du bestemme at dette ikke ville være en god investering fordi nåverdien av annuiteten (59 777,15) er mindre enn det du blir bedt om å betale.