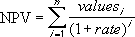NPV, funkcja

Składnia

NPV(stopa;wartość1;wartość2;...)

Stopa  to stopa dyskontowa w okresie jednego okresu.

Wartość1; wartość2,...     to od 1 do 29 argumentów reprezentujących płatności i dochody. Wartość1; wartość2,... muszą być rozmieszczone jednakowo w czasie i występować na końcu każdego okresu. NPV używa kolejności wartości1, wartość2,... interpretować kolejność przepływów gotówkowych. Wartości płatności i dochodów należy koniecznie wprowadzać we właściwej kolejności. Argumenty będące liczbami, wartościami pustymi, wartościami logicznymi lub tekstowymi reprezentacjami liczb są zliczane. Argumenty będące wartościami błędów lub tekstem, których nie można przekształcić w liczby, są ignorowane.

Spostrzeżenia

• Inwestycja w funkcji NPV rozpoczyna się jeden okres przed datą przepływu gotówkowego wartość1, a kończy się wraz z ostatnim przepływem gotówkowym znajdującym się na liście. Obliczenie wartości funkcji NPV jest wykonywane na podstawie przyszłych przepływów gotówkowych. Jeżeli pierwszy przepływ ma miejsce na początku pierwszego okresu, to wartość ta musi być dodana do wyniku NPV, a nie zawarta w wartościach argumentów. Więcej informacji zawierają poniższe przykłady.

• Jeśli n jest liczbą przepływów gotówkowych na liście wartości, zależność na obliczenie funkcji NPV jest następująca:

  

• Funkcja NPV jest podobna do funkcji PV (wartość bieżąca). Podstawowa różnica między funkcjami PV i NPV polega na tym, że funkcja PV pozwala, by przepływy zaczynały się na końcu lub na początku okresu. W odróżnieniu od zmiennych przepływów gotówkowych NPV, przepływy gotówkowe PV muszą być stałe w okresie inwestycji. Więcej informacji o kredytach i funkcjach finansowych zamieszczono w opisie funkcji PV.

Przykład 1

W poniższym przykładzie:

• Stopa to roczna stopa dyskontowa.

• Wartość1 to początkowy koszt inwestycji za rok od dnia dzisiejszego.

• Wartość2 to zwrot z pierwszego roku.

• Wartość3 to zwrot z drugiego roku.

• Wartość4 to zwrot z trzeciego roku.

W tym przykładzie jako jedną z wartości należy podać początkowy koszt w wysokości 10 000 zł, ponieważ płatność następuje na koniec pierwszego okresu.

Przykład 2

W poniższym przykładzie:

• Stopa to roczna stopa dyskontowa. Wartość ta może reprezentować stopę inflacji lub stopę procentową konkurencyjnej inwestycji.

• Wartość1 to początkowy koszt inwestycji za rok od dnia dzisiejszego.

• Wartość2 to zwrot z pierwszego roku.

• Wartość3 to zwrot z drugiego roku.

• Wartość4 to zwrot z trzeciego roku.

• Wartość5 to zwrot z czwartego roku.

• Wartość6 to zwrot z piątego roku.

W tym przykładzie nie podasz początkowego kosztu w wysokości 40 000 zł jako jednej z wartości, ponieważ płatność ma miejsce na początku pierwszego okresu.