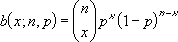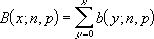Zwraca wartość pojedynczego składnika dwumianowego rozkładu prawdopodobieństwa. Funkcję ROZKŁ.DWUM należy stosować do rozwiązywania problemów, w których występuje stała liczba testów lub prób, wynik każdej próby może być tylko sukcesem lub porażką, próby są niezależne, a prawdopodobieństwo sukcesu jest stałe w trakcie eksperymentu. Na przykład za pomocą funkcji ROZKŁ.DWUM można obliczyć prawdopodobieństwo, że z trojga następnych nowo narodzonych dzieci dwoje będzie płci męskiej.
Składnia
ROZKŁ.DWUM(liczba_s;próby;prawdopodobieństwo_s;skumulowany)
W składni funkcji ROZKŁ.DWUM występują następujące argumenty:
-
Liczba_s Argument wymagany. Liczba sukcesów w próbach.
-
Próby Argument wymagany. Liczba niezależnych prób.
-
Prawdopodobieństwo_s Argument wymagany. Prawdopodobieństwo sukcesu w każdej próbie.
-
Skumulowany Argument wymagany. Wartość logiczna, która określa postać funkcji. Jeśli argument „skumulowany” ma wartość PRAWDA, funkcja ROZKŁ.DWUM zwraca funkcję rozkładu skumulowanego, czyli prawdopodobieństwo, że zachodzi co najwyżej liczba_s sukcesów; jeśli FAŁSZ, zwraca funkcję masy prawdopodobieństwa, czyli prawdopodobieństwo, że zajdzie liczba_s sukcesów.
Spostrzeżenia
-
Argumenty liczba_s i próby są obcinane do liczb całkowitych.
-
Jeśli number_s, prób lub probability_s nie jest liczbą, funkcja BINOM. Funkcja ROZKŁ.#VALUE zwraca wartość! wartość błędu #ADR!.
-
Jeśli number_s < 0 lub number_s > prób, funkcja BINOM. Funkcja ROZKŁ.#NUM zwraca wartość! wartość błędu #ADR!.
-
Jeśli probability_s < 0 lub probability_s > 1, funkcja DWUM. Funkcja ROZKŁ.#NUM zwraca wartość! wartość błędu #ADR!.
-
Funkcja gęstości prawdopodobieństwa dwumianowego przedstawia się następująco:
gdzie:
jest funkcją KOMBINACJE(n;x).
Skumulowany rozkład dwumianowy przedstawia się następująco:
Przykład
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Dane |
Opis |
|
|
6 |
Liczba sukcesów w próbach |
|
|
10 |
Liczba niezależnych prób |
|
|
0,5 |
Prawdopodobieństwo sukcesu w każdej próbie |
|
|
Formuła |
Opis |
Wynik |
|
=ROZKŁ.DWUM(A2;A3;A4;FAŁSZ) |
Prawdopodobieństwo dokładnie 6 sukcesów w 10 próbach |
0,2050781 |