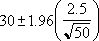Zwraca przedział ufności średniej populacji z rozkładem normalnym. Przedział ufności to zakres po obu stronach średniej próbki. Jeśli na przykład zamówisz produkt pocztą e-mail, możesz określić z określoną pewnością, że najwcześniejszy i najnowszy produkt zostanie nabyty.
Składnia
UFNOŚĆ(alfa;standard_dev;rozmiar)
Alfa to poziom istotności używany do obliczania poziomu ufności. Poziom ufności jest równy 100*(1 – alfa)%, czyli wartość alfa równa 0,05 wskazuje poziom ufności 95%.
Odchylenie_std jest odchyleniem standardowym populacji dla zakresu danych i przyjmuje się, że jest znane.
Rozmiar to rozmiar próbki.
Uwagi
-
Jeśli którykolwiek z argumentów nie jest liczbą, funkcja UFNOŚĆ zwraca #VALUE! wartość błędu #ADR!.
-
Jeśli alfa ≤ 0 lub alfa ≥ 1, funkcja UFNOŚĆ zwraca #NUM! wartość błędu #ADR!.
-
Jeśli standard_dev ≤ 0, funkcja UFNOŚĆ zwraca #NUM! wartość błędu #ADR!.
-
Jeśli argument rozmiar nie jest liczbą całkowitą, to jest obcinany.
-
Jeśli rozmiar < 1, funkcja UFNOŚĆ zwraca #NUM! wartość błędu #ADR!.
-
Jeśli przyjmie się alfa równe 0,05, to trzeba obliczyć obszar pod standardową krzywą normalną, który równy jest (1 - alfa) lub 95%. Wartość ta równa jest ± 1,96. Interwał ufności jest zatem równy:
Przykład
Załóżmy, że w próbie 50 osób dojeżdżających do pracy średnia długość podróży do pracy wynosi 30 minut z odchyleniem standardowym populacji wynoszącym 2,5. Możemy mieć 95 procent pewności, że średnia z populacji znajduje się w interwale:
|
Alfa |
StdDev |
Rozmiar |
Formuła |
Opis (wynik) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=UFNOŚĆ([Alfa];[Odch.Standardowe];[Rozmiar]) |
Interwał ufności średniej populacji. Innymi słowy, średnia długość podróży do pracy wynosi 30 ± 0,692951 minut lub od 29,3 do 30,7 minuty. (0.692951) |