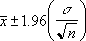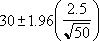Vrne interval zaupanja za a sredino populacije z normalno porazdelitvijo. Interval zaupanja je obseg na obeh strani vzorčne a sredine. Če na primer naročite izdelek po pošti, lahko z določeno stopnjo zanesljivosti določite, najzgodnejši in najnovejši izdelek prispe.
Sintaksa
CONFIDENCE(alfa; standard_dev; velikost)
alfa raven pomembnosti, ki se uporablja za izračun ravni zaupanja. Raven zaupanja je enaka 100*(1 - alfa)% ali drugače povedano – alfa z vrednostjo 0,05 kaže na 95-odstotno raven zaupanja.
standardni_odklon je standardni odklon populacije za obseg podatkov in se predvideva, da je znan.
Velikost velikost vzorca.
Opombe
-
Če kateri od argumentov ni v obliki števila, funkcija CONFIDENCE vrne #VALUE! .
-
Če je argument »≤« 0 ali ≥ 1, vrne CONFIDENCE #NUM! .
-
Če standard_dev ≤ 0, funkcija CONFIDENCE vrne #NUM! .
-
Če argument »velikost« ni celo število, ga program prireže na celo število.
-
Če je < 1, funkcija CONFIDENCE vrne #NUM! .
-
Če privzamemo, da je argument »alfa« enako 0,05, moramo izračunati ploščino pod standardno normalno krivuljo, ki je enaka (1 – »alfa«) ali 95%. Ta vrednost je ± 1.96. Torej je interval zaupanja:
Primer
Denimo, da je v našem vzorcu 50 kommutov povprečna dolžina potovanja do dela 30 minut s standardnim odklonom populacije 2,5. Lahko smo 95-odstotni prepričani, da je a sredina populacije v intervalu:
|
alfa |
StdDev |
Velikost |
Formula |
Opis (rezultat) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENCE([Alfa],[StdDev],[Velikost]) |
Interval zaupanja za aritmetično sredino populacije. Z drugimi besedami, povprečna dolžina potovanja do dela je enaka 30 ± 0,692951 minut ali 29,3 do 30,7 minut. (0.692951) |