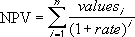NPV (funkcija NPV)

Sintaksa

NPV(mera; vrednost1; vrednost2; ...)

Stopnja     je stopnja popusta v enem obdobju.

vrednost1; vrednost2,...     so 1 do 29 argumentov, ki predstavljajo plačila in dohodke. vrednost1; vrednost2,... morajo biti časovno enakomerno porazdeljene in na koncu vsakega obdobja. NPV vrstni red vrednosti value1, value2,... za določanje vrste denarnih tokov. Pazite, da boste vnašali vrednosti svojih plačil in dohodkov v pravilnem vrstnem redu in s pravilnimi predznaki. Prešteti so argumenti, ki so števila, prazne, logične vrednosti ali besedilne predstavitve števil; Argumenti, ki so vrednosti napak ali besedilo, ki ga ni mogoče prevesti v števila, so prezrti.

Opombe

• Naložba (investicija) NPV se začne eno obdobje pred denarnim tokom za »vrednost1« in se konča z zadnjim denarnim tokom na seznamu. Izračun NPV temelji na prihodnjih denarnih tokovih. Če je prvi denarni tok na začetku prvega obdobja, morate to prvo vrednost dodati rezultatu NPV in je ne vključiti v argumente »vrednost«. Za več informacij si oglejte razlago v spodnjem primeru.

• Če je n število denarnih tokovih na seznamu vrednosti, je formula za NPV:

  

• NPV je podobna funkciji PV (sedanja vrednost). Temeljna razlika med funkcijama PV in NPV je, da PV lahko uporablja denarne tokove, ki se začnejo ob koncu ali pa ob začetku obdobja. V nasprotju s spremenljivimi vrednostmi za denarne tokove v funkciji NPV funkcija PV zahteva, da so denarni tokovi nespremenjeni (konstantni) med trajanjem naložbe. Za informacije o rentah in finančnih funkcijah si oglejte razlago funkcije PV.

1. primer

V tem primeru:

• Mera je letna diskontna stopnja.

• Vrednost1 je začetni strošek naložbe eno leto od danes.

• Vrednost2 je donos s prvega leta.

• Vrednost3 je donos drugega leta.

• Vrednost4 je donos iz tretjega leta.

V tem primeru kot eno od vrednosti vključite začetni strošek 10.000 $, ker je plačilo izvedeno na koncu prvega obdobja.

2. primer

V tem primeru:

• Mera je letna diskontna stopnja. To morda predstavlja stopnjo inflacije ali obrestno mero konkurenčne naložbe.

• Vrednost1 je začetni strošek naložbe eno leto od danes.

• Vrednost2 je donos s prvega leta.

• Vrednost3 je donos drugega leta.

• Vrednost4 je donos iz tretjega leta.

• Vrednost5 je donos iz četrtega leta.

• Vrednost6 je donos s petega leta.

V tem primeru kot eno od vrednosti ne vključite začetnega stroška v višini 40.000 $, ker je plačilo izvedeno na začetku prvega obdobja.