Uporaba reševalca za proračun z veliko začetnicami

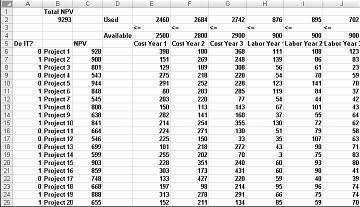
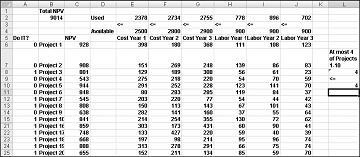
Večina družb si želijo izvajati projekte, ki prispevajo največjo neto sedanjo vrednost (NPV), ob omejenih virih (po navadi kapital in dela). Recimo, da podjetje za razvoj programske opreme poskuša ugotoviti, katere od 20 projektov programske opreme se mora loti. NPV (v milijonih dolarjev) prispeva tako posamezen projekt kot tudi kapital (v milijonih dolarjev) in število programerov, potrebnih v naslednjih treh letih, je podano na delovnem listu »Osnovni model« v datoteki Capbudget.xlsx, ki je prikazano na sliki 30-1 na naslednji strani. Project 2 na primer da 908 milijonov EUR. Med 1. letom zahteva 151 milijonov $, 269 milijonov EUR med 2. letom in 248 milijonov USD med 3. letom. Projekt 2 zahteva 139 programercev med 1. letom, 86 programercev v 2. letu in 83 programerov v 3. letu. Celice E4:G4 kažejo veliko začetnice (v milijonih dolarjev), ki so na voljo v vsakem od treh let, celice H4:J4 pa označujejo, koliko programarjev je na voljo. Na primer, med letom 1 je na voljo do 2,5 milijarde EUR kapitala in 900 programerov.

Podjetje se mora odločiti, ali naj se loti vsakega projekta. Denimo, da ne moremo izvesti le del projekta programske opreme; če bomo dodelili 0,5 od potrebnih sredstev, na primer, bi imeli dela proste program, ki bi nam prinašajo 0 $ prihodkov!

Trik pri modeliranjem situacij, v katerih naredite ali ne naredite nekaj, je uporaba binarnih celic, ki se spreminjajo. Dvojiška celica, ki se spreminja, je vedno enaka 0 ali 1. Ko je dvojiška spreminjajoča se celica, ki ustreza projektu, enaka 1, izvedemo projekt. Če je dvojiška spreminjajoča se celica, ki ustreza projektu, enaka 0, projekta ne bomo spreminjali. Reševalca ste nastavili tako, da uporablja obseg dvojiških celic, ki se spreminjajo, tako, da dodate omejitev – izberite celice, ki se spreminjajo, in nato na seznamu v pogovornem oknu Dodaj omejitev izberite Bin.

S tem ozadjem smo pripravljeni, da rešimo težavo z izbiro projekta programske opreme. Kot vedno pri modelu Reševalca začnete tako, da prepoznamo našo ciljno celico, celice, ki se spreminjajo, in omejitve.

• Ciljna celica. Povečamo NPV, ki ga ustvarijo izbrani projekti.

• Celice, ki se spreminjajo. Za vsak projekt poiščemo dvojiško celico 0 ali 1. Te celice sem najdem v obsegu A6:A25 (in poimenoval obseg pike). Na primer 1 v celici A6 pomeni, da se lotimo projekta 1; vrednost 0 v celici C6 pomeni, da se ne lotimo projekta 1.

• Omejitve. Zagotoviti moramo, da je za vsako leto t (t=1, 2, 3), Uporabljen kapital year t manjši ali enak kot razpoložljivi kapital Year t, uporabljeno leto t dela pa je manjše ali enako številu leto t dela, ki je na voljo.

Kot lahko vidite, mora naš delovni list izračunati za vsak izbor projektov NPV, kapital, uporabljen letno, in programerje, ki so jih uporabili vsako leto. V celici B2 s formulo SUMPRODUCT(doit,NPV) izračunam skupni NPV, ki so ga ustvarili izbrani projekti. (Ime obsega NPV se nanaša na obseg C6:C25.) Za vsak projekt z vrednostjo 1 v stolpcu A ta formula izvede NPV projekta, za vsak projekt z vrednostjo 0 v stolpcu A pa ta formula ne vrne NPV-a projekta. Zato lahko izračunamo NPV vseh projektov, naša ciljna celica pa je linearna, ker je izračunana s seštevanjem izrazov, ki sledijo obrazcu (spreminjanje celice )*(konstanta). Na podoben način izračunam kapital, uporabljen vsako leto, in dela, ki se uporabljajo vsako leto s kopiranjem iz E2 na F2:J2 formulo SUMPRODUCT(doit,E6:E25).

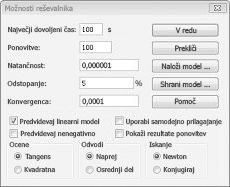
Zdaj izpolnim pogovorno okno Parametri reševalca, kot je prikazano na sliki 30-2.

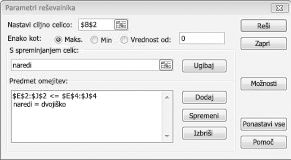
Naš cilj je maksimirati NPV izbranih projektov (celica B2). Naše celice, ki se spreminjajo (obseg z imenom »doit«), so binarne celice, ki se spreminjajo za vsak projekt. Omejitev E2:J2<=E4:J4 zagotavlja, da so v posameznem letu uporabljeni kapital in delo manjši ali enaki razpoložljivem kapitalu in delu. Če želite dodati omejitev, zaradi katere so celice, ki se spreminjajo, dvojiške, v pogovornem oknu Parametri reševalca kliknite Dodaj in na sredini pogovornega okna na seznamu izberite Regal. Pogovorno okno Dodaj omejitev bi moralo biti prikazano, kot je prikazano na sliki 30-3.

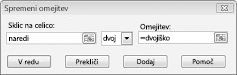
Naš model je linearen, ker je ciljna celica izračunana kot vsota izrazov, ki imajo obliko (spreminjanje celice )*( konstanta) in ker so omejitve uporabe virov izračunane s primerjavo vsote (spreminjanih celic )*(konstant) s konstanto.

Ko je pogovorno okno Parametri reševalca izpolnjeno, kliknite Reši in rezultati so prikazani na sliki 30-1. Podjetje lahko z izbiro možnosti Projekti 2, 3, 6–10, 14–16, 19 in 20 pridobi največ NPV v višini 9.293 milijonov EUR (9,293 milijarde EUR).

Včasih imajo modeli izbire projektov druge omejitve. Če na primer izberemo Project 3, moramo izbrati tudi Project 4. Ker naša trenutna optimalna rešitev izbere Project 3, ne pa tudi programa Project 4, vemo, da naša trenutna rešitev ne more ostati optimalna. Če želite odpraviti to težavo, preprosto dodajte omejitev, da je dvojiška spreminjajoča se celica za Project 3 manjša ali enaka dvojiški spreminjajoča se celica za Project 4.

Ta primer najdete na delovnem listu Če 3 in nato 4 v Capbudget.xlsx, ki je prikazan na sliki 30-4. Celica L9 se sklicuje na binarno vrednost, ki je povezana s programom Project 3, in celico L12 na binarno vrednost, povezano s Projectom 4. Če dodate omejitev L9<=L12, če izberemo Project 3, je L9 enak 1, naša omejitev pa prisili L12 (dvojiški program Project 4), da je enak 1. Če ne izberemo programa Project 3, mora naša omejitev pustiti binarno vrednost tudi v spreminjajočni celici Programa Project 4. Če ne izberemo Programa Project 3, je L9 enak 0, naša omejitev pa omogoča, da je dvojiški program Project 4 enak 0 ali 1, kar želimo. Nova optimalna raztopina je prikazana na sliki 30-4.

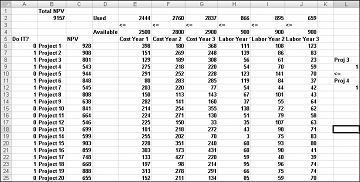
Če izberete Project 3, je izračunana nova optimalna rešitev, ki pomeni, da moramo izbrati tudi Project 4. Recimo, da lahko od projektov od 1 do 10 izvedemo le štiri projekte. (Glejte delovni list »Največ 4 od P1–P10 «, prikazan na sliki 30–5.) V celici L8 izračunamo vsoto dvojiških vrednosti, povezanih s projekti od 1 do 10, s formulo SUM(A6:A15). Nato dodamo omejitev L8<=L10, ki zagotavlja, da je izbranih največ 4 od prvih 10 projektov. Nova optimalna raztopina je prikazana na sliki 30-5. NPV je padel na 9,014 milijarde $.

Modeli linearnega reševalca, pri katerih morajo biti nekatere ali vse celice, ki se spreminjajo, dvojiške ali celo število, običajno težje rešijo kot linearne modele, v katerih je dovoljeno, da so vse celice, ki se spreminjajo, ulomke. Zato smo pogosto zadovoljni s skoraj optimalno rešitvijo binarnega ali celega programskega problema. Če se vaš model Reševalca izvaja dlje časa, vam priporočamo, da v pogovornem oknu Možnosti reševalca prilagodite nastavitev Tolerance. (Glejte sliko 30–6.) Nastavitev tolerance 0,5 % na primer pomeni, da se bo reševalec ustavil, ko prvič najde izvedljivo rešitev, ki je v 0,5 odstotkih teoretične optimalne vrednosti ciljne celice (teoretična optimalna ciljna vrednost celice je optimalna ciljna vrednost, ki jo najdemo, ko izpustite binarne in celoštevilske omejitve). Pogosto se soočamo z izbiro med iskanjem odgovora v roku 10 odstotkov optimalne v 10 minutah ali iskanjem optimalne rešitve v dveh tednih računalniškega časa! Privzeta vrednost Tolerance je 0,05 %, kar pomeni, da reševalec preneha, ko najde vrednost ciljne celice v obsegu 0,05 odstotka teoretične optimalne vrednosti ciljne celice.

1. Podjetje ima 9 projektov, ki so upoštevani. NPV, ki ga doda vsak projekt, in kapital, ki ga zahteva posamezen projekt v naslednjih dveh letih, je prikazan v spodnji tabeli. (Vse številke so v milijonih.) Project 1 bo na primer prištel 14 milijonov EUR V NPV-je in zahteval odhodke v vrednosti 12 milijonov EUR med 1. letom in 3 milijone EUR med 2. letom. V 1. letu je za projekte na voljo 50 milijonov EUR kapitala, med 2. letom pa je na voljo 20 milijonov EUR.

	NPV	Odhodki za leto 1	Odhodki za leto 2
Project 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	12	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Kako lahko maksimiziramo NPV, če ne moremo izvesti le del projekta, vendar se moramo loti nobenega projekta ali pa ne?

• Recimo, da je treba v primeru projekta 4 izvesti projekt 5. Kako lahko maksimiziramo NPV?

• Podjetje za objavljanje poskuša ugotoviti, kateri od 36 knjig naj bi objavilo to leto. V datoteki Pressdata.xlsx te informacije o posamezni knjigi:

  • Projiciranje prihodkov in razvojnih stroškov (v tisočih dolarjev)

  • Strani v posamezni knjigi

  • Ali je knjiga nastavljena za občinstvo razvijalcev programske opreme (navedeno z 1 v stolpcu E)

    Podjetje za objavljanje lahko objavi knjige, ki v tem letu skupaj dodajo do 8500 strani, objaviti pa mora vsaj štiri knjige, ki so prilagojene razvijalcem programske opreme. Kako lahko podjetje maksimizira svoj dobiček?

Ta članek je iz analize podatkov in poslovnega modeliranja programa Microsoft Office Excel 2007 prilagodil Wayne L. Winston.

Ta knjiga razredni slog je bila razvita iz serije predstavitev, ki jih Wayne Winston, dobro znan statisticijan in poslovnega profesorja, ki je specializes v ustvarjalnih, praktičnih uporabah Excela.