การใช้ Solver เพื่อกําหนดการผสมผลิตภัณฑ์ที่เหมาะสม

ฉันจะกําหนดส่วนผสมของผลิตภัณฑ์รายเดือนที่เพิ่มความสามารถในการทํากําไรให้ได้สูงสุดได้อย่างไร

บริษัทมักจะต้องกําหนดปริมาณของแต่ละผลิตภัณฑ์เพื่อผลิตเป็นรายเดือน ในรูปแบบที่ง่ายที่สุดปัญหา การผสมผลิตภัณฑ์ เกี่ยวข้องกับวิธีการกําหนดปริมาณของแต่ละผลิตภัณฑ์ที่ควรผลิตในช่วงเดือนเพื่อเพิ่มผลกําไรสูงสุด การผสมผลิตภัณฑ์มักจะเป็นไปตามข้อจํากัดต่อไปนี้:

• การผสมผลิตภัณฑ์ไม่สามารถใช้ทรัพยากรมากกว่าที่มีอยู่ได้

• มีความต้องการที่ จํากัด สําหรับแต่ละผลิตภัณฑ์ เราไม่สามารถผลิตผลิตภัณฑ์ได้มากกว่าจํานวนเดือนมากกว่าการสั่งการเนื่องจากการผลิตส่วนเกินเสีย (ตัวอย่างเช่นยาที่เน่าเสียได้)

ตอนนี้เรามาแก้ไขตัวอย่างต่อไปนี้ของปัญหาการผสมผลิตภัณฑ์ คุณสามารถหาวิธีแก้ไขปัญหานี้ได้ในไฟล์ Prodmix.xlsx ที่แสดงในรูป 27-1

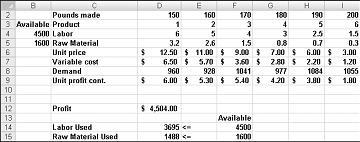
สมมติว่าเราทํางานให้กับ บริษัท ยาที่ผลิตผลิตภัณฑ์ต่าง ๆ หกรายการที่โรงงานของพวกเขา การผลิตแต่ละผลิตภัณฑ์ต้องใช้แรงงานและวัตถุดิบ แถวที่ 4 ในรูปที่ 27-1 แสดงชั่วโมงแรงงานที่จําเป็นในการผลิตแต่ละผลิตภัณฑ์และแถวที่ 5 แสดงปอนด์ของวัตถุดิบที่จําเป็นในการผลิตปอนด์ของแต่ละผลิตภัณฑ์ ตัวอย่างเช่นการผลิตปอนด์ของผลิตภัณฑ์ 1 ต้องใช้แรงงานหกชั่วโมงและวัตถุดิบ 3.2 ปอนด์ สําหรับยาแต่ละตัวราคาต่อปอนด์จะได้รับในแถวที่ 6 ต้นทุนต่อหน่วยต่อปอนด์จะได้รับในแถวที่ 7 และการจัดสรรกําไรต่อปอนด์จะให้ในแถวที่ 9 ตัวอย่างเช่น ผลิตภัณฑ์ 2 ขายในราคา $11.00 ต่อปอนด์ จะมีราคาต่อหน่วย $5.70 ต่อปอนด์ และให้กําไร $5.30 ต่อปอนด์ ความต้องการของเดือนสําหรับยาแต่ละตัวจะได้รับในแถวที่ 8 ตัวอย่างเช่น ความต้องการผลิตภัณฑ์ 3 คือ 1041 ปอนด์ เดือนนี้, 4500 ชั่วโมงของแรงงานและ 1600 ปอนด์ของวัตถุดิบที่มีอยู่ของ บริษัทนี้สามารถเพิ่มผลกําไรรายเดือนได้อย่างไร?

ถ้าเราไม่ทราบอะไรเกี่ยวกับ Excel Solver เราจะโจมตีปัญหานี้โดยการสร้างเวิร์กชีตเพื่อติดตามกําไรและการใช้ทรัพยากรที่เกี่ยวข้องกับผลิตภัณฑ์ผสม จากนั้นเราจะใช้การทดลองและข้อผิดพลาดที่จะแตกต่างกันไปผสมผลิตภัณฑ์เพื่อเพิ่มผลกําไรโดยไม่ต้องใช้แรงงานหรือวัตถุดิบมากกว่าที่มีอยู่และไม่มีการผลิตยาใด ๆ ที่เกินความต้องการ เราใช้ Solver ในกระบวนการนี้เฉพาะในขั้นตอนการทดลองใช้และข้อผิดพลาดเท่านั้น โดยหลักแล้ว Solver คือเครื่องมือการปรับให้เหมาะสมที่ดําเนินการค้นหาเวอร์ชันทดลองใช้และข้อผิดพลาดได้อย่างราบรื่น

สิ่งสําคัญในการแก้ปัญหาการผสมผลิตภัณฑ์คือการคํานวณการใช้ทรัพยากรและกําไรที่เกี่ยวข้องกับการผสมผลิตภัณฑ์ใดๆ ที่กําหนดอย่างมีประสิทธิภาพ เครื่องมือสําคัญที่เราสามารถใช้เพื่อทําการคํานวณนี้คือฟังก์ชั่น SUMPRODUCT ฟังก์ชัน SUMPRODUCT จะคูณค่าที่สอดคล้องกันในช่วงของเซลล์ และส่งกลับผลรวมของค่าเหล่านั้น ช่วงเซลล์แต่ละช่วงที่ใช้ในการประเมิน SUMPRODUCT ต้องมีขนาดเดียวกัน ซึ่งหมายความว่าคุณสามารถใช้ SUMPRODUCT ที่มีสองแถวหรือสองคอลัมน์ได้ แต่ไม่ใช่กับหนึ่งคอลัมน์และหนึ่งแถว

เป็นตัวอย่างของวิธีที่เราสามารถใช้ฟังก์ชัน SUMPRODUCT ในตัวอย่างการผสมผลิตภัณฑ์ของเรา ลองลองคํานวณการใช้ทรัพยากรของเรา การใช้แรงงานของเราคํานวณโดย

(แรงงานใช้ต่อปอนด์ของยาเสพติด 1)*(ยาเสพติด 1 ปอนด์ผลิต)+
(แรงงานใช้ต่อปอนด์ของยาเสพติด 2)*(ยาเสพติด 2 ปอนด์ที่ผลิต) +
(แรงงานใช้ต่อปอนด์ของยาเสพติด 6)*(ยาเสพติด 6 ปอนด์ผลิต)

เราสามารถคํานวณการใช้แรงงานในรูปแบบที่น่าเบื่อกว่าเช่น D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4 ในทํานองเดียวกัน การใช้วัตถุดิบอาจถูกคํานวณเป็น D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5 อย่างไรก็ตาม การใส่สูตรเหล่านี้ลงในเวิร์กชีตสําหรับผลิตภัณฑ์หกรายการนั้นต้องใช้เวลานาน ลองนึกภาพว่าใช้เวลานานเท่าใดหากคุณทํางานกับ บริษัท ที่ผลิตตัวอย่างเช่น 50 ผลิตภัณฑ์ที่โรงงานของพวกเขา วิธีที่ง่ายกว่ามากในการคํานวณการใช้แรงงานและวัตถุดิบคือการคัดลอกจาก D14 ถึง D15 สูตร SUMPRODUCT ($D $ 2:$I $ 2,D4:I4) สูตรนี้คํานวณ D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (ซึ่งเป็นการใช้แรงงานของเรา) แต่จะใส่ได้ง่ายกว่ามาก! โปรดสังเกตว่าฉันใช้เครื่องหมาย $ กับช่วง D2:I2 ดังนั้นเมื่อฉันคัดลอกสูตรฉันยังคงจับภาพผสมผลิตภัณฑ์จากแถว 2 สูตรในเซลล์ D15 จะคํานวณการใช้วัตถุดิบ

ในทํานองเดียวกันกําไรของเราจะถูกกําหนดโดย

(ยาเสพติด 1 กําไรต่อปอนด์)* (ยาเสพติด 1 ปอนด์ที่ผลิต) +
(ยาเสพติด 2 กําไรต่อปอนด์)* (ยาเสพติด 2 ปอนด์ที่ผลิต) + ...
(ยาเสพติด 6 กําไรต่อปอนด์)*(ผลิตยาเสพติด 6 ปอนด์)

กําไรสามารถคํานวณได้อย่างง่ายดายในเซลล์ D12 ด้วยสูตร SUMPRODUCT(D9:I9,$D$2:$I$2)

ตอนนี้เราสามารถระบุองค์ประกอบสามอย่างของรูปแบบ Solver ผสมผลิตภัณฑ์ของเรา

• เซลล์เป้าหมาย เป้าหมายของเราคือการเพิ่มผลกําไร (คํานวณในเซลล์ D12)

• การเปลี่ยนเซลล์ จํานวนปอนด์ที่ผลิตของแต่ละผลิตภัณฑ์ (แสดงรายการในช่วงเซลล์ D2:I2)

• ข้อจํากัด เรามีข้อจํากัดต่อไปนี้:

  • อย่าใช้แรงงานหรือวัตถุดิบมากกว่าที่มีอยู่ นั่นคือ ค่าในเซลล์ D14:D15 (ทรัพยากรที่ใช้) ต้องน้อยกว่าหรือเท่ากับค่าในเซลล์ F14:F15 (ทรัพยากรที่พร้อมใช้งาน)

  • อย่าผลิตยามากกว่าความต้องการ นั่นคือค่าในเซลล์ D2:I2 (ปอนด์ที่ผลิตของแต่ละยา) จะต้องน้อยกว่าหรือเท่ากับความต้องการสําหรับแต่ละยา (ระบุไว้ในเซลล์ D8:I8)

  • เราไม่สามารถผลิตยาในปริมาณติดลบได้

ฉันจะแสดงวิธีการใส่เซลล์เป้าหมาย การเปลี่ยนเซลล์ และข้อจํากัดลงใน Solver จากนั้นสิ่งที่คุณต้องทําคือคลิกปุ่ม Solve เพื่อค้นหาส่วนผสมผลิตภัณฑ์ที่เพิ่มผลกําไรให้มากที่สุด!

เมื่อต้องการเริ่มต้น ให้คลิกแท็บ ข้อมูล และในกลุ่ม วิเคราะห์ ให้คลิก Solver

กล่องโต้ตอบ Solver Parameters จะปรากฏขึ้นตามที่แสดงในรูป 27-2

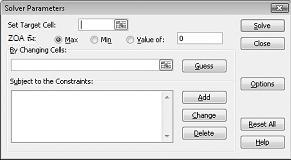
คลิกกล่อง ตั้งค่าเซลล์เป้าหมาย แล้วเลือกเซลล์กําไรของเรา (เซลล์ D12) คลิกกล่อง โดยการเปลี่ยนเซลล์ แล้วชี้ไปที่ช่วง D2:I2 ซึ่งมีปอนด์ที่ผลิตของแต่ละยา ขณะนี้กล่องโต้ตอบควรมีลักษณะเป็น รูป 27-3

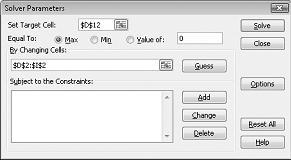
ตอนนี้เราพร้อมแล้วที่จะเพิ่มข้อจํากัดให้กับตัวแบบ คลิกปุ่ม เพิ่ม คุณจะเห็นกล่องโต้ตอบ เพิ่มข้อจํากัด แสดงใน รูป 27-4

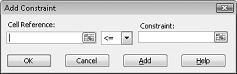
เมื่อต้องการเพิ่มข้อจํากัดการใช้ทรัพยากร ให้คลิกกล่อง การอ้างอิงเซลล์ แล้วเลือกช่วง D14:D15 เลือก <= จากรายการตรงกลาง คลิกกล่อง ข้อจํากัด แล้วเลือกช่วงเซลล์ F14:F15 ในตอนนี้ กล่องโต้ตอบ เพิ่มข้อจํากัด ควรมีลักษณะเหมือนรูปที่ 27-5

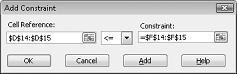
ขณะนี้เราได้ทําให้แน่ใจว่าเมื่อ Solver พยายามหาค่าที่แตกต่างกันสําหรับเซลล์ที่เปลี่ยนแปลง เฉพาะการผสมที่ตอบสนองทั้ง D14<=F14 (ค่าแรงที่ใช้น้อยกว่าหรือเท่ากับค่าแรงที่ใช้ได้) และ D15<=F15 (วัตถุดิบที่ใช้น้อยกว่าหรือเท่ากับวัตถุดิบที่พร้อมใช้งาน) จะถูกพิจารณา คลิก เพิ่ม เพื่อใส่ข้อจํากัดความต้องการ กรอกข้อมูลในกล่องโต้ตอบ เพิ่มข้อจํากัด ตามที่แสดงใน รูป 27-6

การเพิ่มข้อจํากัดเหล่านี้จะทําให้แน่ใจได้ว่าเมื่อ Solver พยายามผสมค่าของเซลล์ที่เปลี่ยนแปลงที่แตกต่างกัน เฉพาะการผสมที่เป็นไปตามพารามิเตอร์ต่อไปนี้เท่านั้นที่จะถูกพิจารณา:

• D2<=D8 (ปริมาณที่ผลิตของยาเสพติด 1 น้อยกว่าหรือเท่ากับความต้องการยาเสพติด 1)

• E2<=E8 (ปริมาณการผลิตยาเสพติด 2 น้อยกว่าหรือเท่ากับอุปสงค์สําหรับยาเสพติด 2)

• F2<=F8 (ปริมาณที่ผลิตของยาเสพติด 3 น้อยกว่าหรือเท่ากับความต้องการยาเสพติด 3)

• G2<=G8 (ปริมาณที่ผลิตของยาเสพติด 4 น้อยกว่าหรือเท่ากับความต้องการยาเสพติด 4)

• H2<=H8 (ปริมาณที่ผลิตของยาเสพติด 5 น้อยกว่าหรือเท่ากับความต้องการยาเสพติด 5)

• I2<=I8 (ปริมาณที่ผลิตของยาเสพติด 6 น้อยกว่าหรือเท่ากับความต้องการยาเสพติด 6)

คลิก ตกลง ในกล่องโต้ตอบ เพิ่มข้อจํากัด หน้าต่าง Solver ควรมีลักษณะเหมือนกับรูปภาพ 27-7

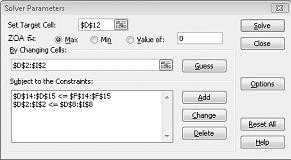
เราใส่ข้อจํากัดที่เปลี่ยนเซลล์จะต้องไม่เป็นค่าลบในกล่องโต้ตอบ ตัวเลือกของ Solver คลิกปุ่ม ตัวเลือก ในกล่องโต้ตอบ พารามิเตอร์ Solver เลือกกล่อง สมมติรูปแบบเชิงเส้น และกล่อง สมมติว่าไม่ใช่ค่าลบ ตามที่แสดงในรูปที่ 27-8 ในหน้าถัดไป คลิก ตกลง

การเลือกกล่อง สมมติว่าไม่ใช่ค่าลบ จะทําให้แน่ใจได้ว่า Solver จะพิจารณาเฉพาะการผสมของเซลล์ที่เปลี่ยนแปลงซึ่งแต่ละเซลล์จะถือว่ามีค่าที่ไม่เป็นลบ เราได้ตรวจสอบกล่องสมมติว่ารูปแบบเชิงเส้นเนื่องจากปัญหาการผสมผลิตภัณฑ์เป็นปัญหา Solver ชนิดพิเศษที่เรียกว่ารูปแบบเชิงเส้น โดยหลักแล้ว Solver รุ่นจะเป็นเชิงเส้นภายใต้เงื่อนไขต่อไปนี้:

• เซลล์เป้าหมายจะถูกคํานวณโดยการเพิ่มเงื่อนไขของฟอร์ม (เซลล์ที่เปลี่ยนแปลง)*(ค่าคงที่) ไว้ด้วยกัน

• ข้อจํากัดแต่ละข้อเป็นไปตาม "ข้อกําหนดของรูปแบบเชิงเส้น" ซึ่งหมายความว่าแต่ละข้อจํากัดจะถูกประเมินโดยการรวมเงื่อนไขของฟอร์ม (เซลล์ที่เปลี่ยนแปลง)*(ค่าคงที่) และการเปรียบเทียบผลรวมกับค่าคงที่

เหตุใดปัญหา Solver จึงเป็นเชิงเส้น เซลล์เป้าหมายของเรา (กําไร) ถูกคํานวณเป็น

(ยาเสพติด 1 กําไรต่อปอนด์)* (ยาเสพติด 1 ปอนด์ที่ผลิต) +
(ยาเสพติด 2 กําไรต่อปอนด์)* (ยาเสพติด 2 ปอนด์ที่ผลิต) + ...
(ยาเสพติด 6 กําไรต่อปอนด์)*(ผลิตยาเสพติด 6 ปอนด์)

การคํานวณนี้เป็นไปตามรูปแบบที่ค่าของเซลล์เป้าหมายได้รับมาโดยการเพิ่มเงื่อนไขของฟอร์ม (การเปลี่ยนเซลล์)*(ค่าคงที่) ไว้ด้วยกัน

ข้อจํากัดด้านแรงงานของเราถูกประเมินโดยการเปรียบเทียบค่าที่ได้จาก (แรงงานที่ใช้ต่อปอนด์ของยาเสพติด 1)*(ผลิตยาเสพติด 1 ปอนด์) + (แรงงานที่ใช้ต่อปอนด์ของยาเสพติด 2)*(ยา 2 ปอนด์ผลิต)+ (แรงงานเราed ต่อปอนด์ของยาเสพติด 6)*(ยาเสพติด 6 ปอนด์ผลิต) เพื่อแรงงานที่มีอยู่.

ดังนั้นข้อจํากัดแรงงานจะถูกประเมินโดยการรวมกันเงื่อนไขของแบบฟอร์ม (เซลล์ที่เปลี่ยน)* (ค่าคงที่) และการเปรียบเทียบผลรวมกับค่าคงที่ ข้อจํากัดแรงงานและข้อจํากัดวัตถุดิบเป็นไปตามข้อกําหนดของแบบจําลองเชิงเส้น

ข้อจํากัดความต้องการของเราจะนําฟอร์มไปใช้

(ผลิตยาเสพติด 1)<=(ยาเสพติด 1 ความต้องการ)
(ผลิตยาเสพติด 2)<=(ยาเสพติด 2 อุปสงค์)
§
(ยาเสพติด 6 ผลิต)<=(ยาเสพติด 6 อุปสงค์)

ข้อจํากัดความต้องการแต่ละข้อยังเป็นไปตามข้อกําหนดของรูปแบบเชิงเส้นด้วย เนื่องจากแต่ละข้อจํากัดจะได้รับการประเมินโดยการเพิ่มเงื่อนไขของฟอร์ม (การเปลี่ยนเซลล์)*(ค่าคงที่) ไว้ด้วยกัน และการเปรียบเทียบผลรวมกับค่าคงที่

แสดงให้เห็นว่าผลิตภัณฑ์ของเราผสมรูปแบบเป็นรูปแบบเชิงเส้น, ทําไมเราควรจะดูแลหรือไม่

• ถ้ารูปแบบ Solver เป็นแบบเชิงเส้น และเราเลือก สมมติรูปแบบเชิงเส้น Solver จะรับประกันว่าจะหาโซลูชันที่เหมาะสมที่สุดสําหรับรูปแบบ Solver ถ้า Solver รุ่นไม่เป็นเชิงเส้น Solver อาจพบหรือไม่พบโซลูชันที่เหมาะสม

• ถ้ารูปแบบ Solver เป็นแบบเชิงเส้น และเราเลือก สมมติรูปแบบเชิงเส้น Solver จะใช้อัลกอริทึมที่มีประสิทธิภาพมาก (วิธี simplex) เพื่อค้นหาโซลูชันที่ดีที่สุดของโมเดล ถ้ารูปแบบ Solver เป็นแบบเชิงเส้น และเราไม่ได้เลือกสมมติว่ารูปแบบเชิงเส้น Solver ใช้อัลกอริทึมที่ไม่มีประสิทธิภาพมาก (วิธีการ GRG2) และอาจมีปัญหาในการค้นหาโซลูชันที่ดีที่สุดของโมเดล

หลังจากคลิก ตกลง ในกล่องโต้ตอบ ตัวเลือก Solver เราจะกลับไปยังกล่องโต้ตอบ Solver หลัก ซึ่งแสดงไว้ก่อนหน้าในรูปที่ 27-7 เมื่อเราคลิก Solve แล้ว Solver จะคํานวณโซลูชันที่เหมาะสมที่สุด (ถ้ามีอยู่) สําหรับรุ่นผสมของผลิตภัณฑ์ของเรา ตามที่ฉันระบุไว้ในบทที่ 26 โซลูชันที่เหมาะสมกับรุ่นผลิตภัณฑ์ผสมจะเป็นชุดของค่าเซลล์ที่เปลี่ยนแปลง (ปอนด์ที่ผลิตจากยาแต่ละตัว) ที่เพิ่มผลกําไรสูงสุดจากชุดโซลูชันที่เป็นไปได้ทั้งหมด โซลูชันที่เป็นไปได้คือชุดของการเปลี่ยนแปลงค่าเซลล์ที่สอดคล้องกับข้อจํากัดทั้งหมด การเปลี่ยนค่าเซลล์ที่แสดงในรูปที่ 27-9 เป็นโซลูชันที่เป็นไปได้ เนื่องจากระดับการผลิตทั้งหมดไม่ใช่ค่าลบ ระดับการผลิตไม่เกินความต้องการ และการใช้ทรัพยากรไม่เกินทรัพยากรที่มีอยู่

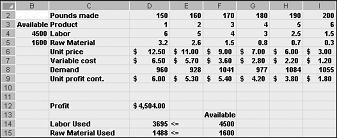
การเปลี่ยนค่าเซลล์ที่แสดงในรูปที่ 27-10 ในหน้าถัดไปแสดง ถึงโซลูชันที่ไม่สามารถแก้ไขได้ด้วย สาเหตุต่อไปนี้:

• เราผลิตเพิ่มเติมของยาเสพติด 5 กว่าความต้องการสําหรับมัน

• เราใช้แรงงานมากกว่าที่มีอยู่

• เราใช้วัตถุดิบมากกว่าที่มีอยู่

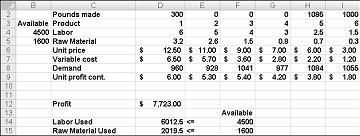
หลังจากคลิก Solver จะค้นหาโซลูชันที่เหมาะสมที่แสดงในรูปที่ 27-11 อย่างรวดเร็ว คุณต้องเลือก Keep Solver Solution เพื่อรักษาค่าโซลูชันที่เหมาะสมที่สุดในเวิร์กชีต

บริษัทยาของเราสามารถเพิ่มผลกําไรรายเดือนได้สูงสุดที่ระดับ 6,625.20 ดอลลาร์โดยการผลิตยา 596.67 ปอนด์ของยาเสพติด 4, 1084 ปอนด์ของยาเสพติด 5 และไม่ใช่ยาอื่น ๆ! เราไม่สามารถระบุได้ว่าเราสามารถทํากําไรได้สูงสุด $6,625.20 ด้วยวิธีอื่นหรือไม่ ทั้งหมดที่เราสามารถมั่นใจได้คือด้วยทรัพยากรและความต้องการที่ จํากัด ของเราไม่มีวิธีที่จะทําให้มากกว่า $ 6,627.20 ในเดือนนี้