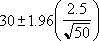ส่งกลับค่าช่วงความเชื่อมั่นของค่าเฉลี่ยประชากรที่มีการแจกแจงปกติ ช่วงความเชื่อมั่นคือช่วงบนด้านใดด้านหนึ่งของค่าเฉลี่ยตัวอย่าง ตัวอย่างเช่น หากคุณสั่งซื้อผลิตภัณฑ์ผ่านทางจดหมาย คุณสามารถกําหนดระดับความเชื่อมั่นที่เฉพาะเจาะจงผลิตภัณฑ์ที่เร็วที่สุดและล่าสุดจะมาถึง
ไวยากรณ์
CONFIDENCE(alpha,standard_dev,size)
แอลฟา คือระดับนัยสําคัญที่ใช้ในการคํานวณระดับความเชื่อมั่น ระดับความเชื่อมั่นเท่ากับ 100*(1 - alpha)% หรืออีกนัยหนึ่ง คือ alpha 0.05 จะระบุระดับความเชื่อมั่น 95 เปอร์เซ็นต์
Standard_dev คือค่าเบี่ยงเบนมาตรฐานของประชากรสําหรับช่วงข้อมูล และถือว่าเป็นที่ทราบ
ขนาด คือขนาดตัวอย่าง
ข้อสังเกต
-
ถ้ามีอาร์กิวเมนต์ใดไม่ใช่ตัวเลข ฟังก์ชัน CONFIDENCE จะส่งกลับ #VALUE! เป็นค่าความผิดพลาด
-
ถ้า alpha ≤ 0 หรือ alpha ≥ 1 ฟังก์ชัน CONFIDENCE จะส่งกลับ #NUM! เป็นค่าความผิดพลาด
-
ถ้า standard_dev ≤ 0 ฟังก์ชัน CONFIDENCE จะส่งกลับ #NUM! เป็นค่าความผิดพลาด
-
ถ้า size ไม่เป็นจำนวนเต็ม จะถูกปัดเศษ
-
ถ้า size < 1 ฟังก์ชัน CONFIDENCE จะส่งกลับ #NUM! เป็นค่าความผิดพลาด
-
ถ้าเราสมมติให้ alpha เท่ากับ 0.05 เราจําเป็นต้องคํานวณพื้นที่ภายใต้เส้นโค้งปกติมาตรฐานที่เท่ากับ (1 - alpha) หรือ 95 เปอร์เซ็นต์ ค่านี้± 1.96 ดังนั้น ช่วงความเชื่อมั่นจึงเป็น:
ตัวอย่าง
สมมติว่าเราสังเกตเห็นว่าในตัวอย่างของ 50 นักเดินทางของเราความยาวเฉลี่ยของการเดินทางไปทํางานคือ 30 นาทีโดยมีค่าเบี่ยงเบนมาตรฐานประชากรเท่ากับ 2.5 เราสามารถมั่นใจได้ 95 เปอร์เซ็นต์ว่าค่าเฉลี่ยประชากรอยู่ในช่วง:
|
แอลฟา |
StdDev |
ขนาด |
สูตร |
คำอธิบาย (ผลลัพธ์) |
|---|---|---|---|---|
|
0.05 |
.5 |
50 |
=CONFIDENCE([Alpha],[StdDev],[ขนาด]) |
ช่วงความเชื่อมั่นของค่าเฉลี่ยประชากร กล่าวอีกนัยหนึ่งความยาวเฉลี่ยของการเดินทางเพื่อทํางานเท่ากับ 30 ± 0.692951 นาทีหรือ 29.3 ถึง 30.7 นาที (0.692951) |