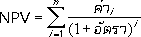คำนวณมูลค่าปัจจุบันสุทธิของเงินลงทุน โดยใช้อัตราส่วนลด ชุดข้อมูลของการชำระเงิน (ค่าเป็นลบ) และรายได้ในอนาคต (ค่าเป็นบวก)
ไวยากรณ์
NPV(rate,value1,value2,...)
อัตรา คืออัตราส่วนลดตลอดระยะเวลาหนึ่ง
Value1, value2,... คืออาร์กิวเมนต์ 1 ถึง 29 ที่แสดงการชําระเงินและรายได้ Value1, value2,... ต้องเว้นวรรคให้เท่าๆ กันในเวลาและเกิดขึ้นเมื่อสิ้นสุดแต่ละช่วงเวลา NPV ใช้ลําดับของ value1, value2,... เพื่อตีความลําดับของกระแสเงินสด ตรวจสอบให้แน่ใจว่าใส่ค่าการชําระเงินและรายได้ของคุณตามลําดับที่ถูกต้อง อาร์กิวเมนต์ที่เป็นตัวเลข ค่าว่าง ค่าตรรกะ หรือข้อความที่ใช้แทนจํานวนจะถูกนับ อาร์กิวเมนต์ที่เป็นค่าความผิดพลาดหรือข้อความที่ไม่สามารถแปลเป็นตัวเลขจะถูกละเว้น
ข้อสังเกต
-
การลงทุน NPV จะเริ่มต้นหนึ่งงวดก่อนวันที่ของกระแสเงินสด value1 และสิ้นสุดด้วยกระแสเงินสดสุดท้ายในรายการ การคํานวณ NPV ขึ้นอยู่กับกระแสเงินสดในอนาคต ถ้ากระแสเงินสดแรกของคุณเกิดขึ้นในตอนต้นของคาบเวลาแรก ค่าแรกต้องถูกเพิ่มลงในผลลัพธ์ NPV ไม่รวมอยู่ในอาร์กิวเมนต์ value สําหรับข้อมูลเพิ่มเติม โปรดดูตัวอย่างด้านล่าง
-
ถ้า n เป็นจำนวนกระแสเงินสดในรายการ value จะได้สูตรสำหรับ NPV ดังนี้
-
NPV จะคล้ายกับฟังก์ชัน PV (มูลค่าปัจจุบัน) ผลต่างหลักระหว่าง PV และ NPV คือ PV อนุญาตให้กระแสเงินสดเริ่มต้นที่ตอนท้ายหรือต้นงวดได้ กระแสเงินสด PV ต้องเป็นค่าคงที่ตลอดการลงทุน ซึ่งต่างจากค่าผันแปร NPV กระแสเงินสด สําหรับข้อมูลเกี่ยวกับฟังก์ชันเงินรายปีและการเงิน ให้ดูที่ ฟังก์ชัน PV
ตัวอย่าง 1
ในตัวอย่างต่อไปนี้:
-
Rate คืออัตราส่วนลดรายปี
-
Value1 คือต้นทุนเริ่มต้นของการลงทุนหนึ่งปีนับจากวันนี้
-
Value2 คือผลตอบแทนจากปีแรก
-
Value3 คือผลตอบแทนจากปีที่สอง
-
Value4 คือผลตอบแทนจากปีที่สาม
ในตัวอย่าง คุณจะรวมค่าใช้จ่าย $10,000 เริ่มต้นเป็นหนึ่งในค่า เนื่องจากการชําระเงินจะเกิดขึ้นเมื่อสิ้นสุดช่วงเวลาแรก
|
อัตรา |
ค่า 1 |
ค่า 2 |
ค่า 3 |
ค่า 4 |
สูตร |
คำอธิบาย (ผลลัพธ์) |
|---|---|---|---|---|---|---|
|
10% |
-10000 |
3000 |
4200 |
6800 |
=NPV([Rate], [Value1], [Value2], [Value3], [Value4]) |
มูลค่าปัจจุบันสุทธิของการลงทุนนี้ (1,188.44) |
ตัวอย่าง 2
ในตัวอย่างต่อไปนี้:
-
Rate คืออัตราส่วนลดรายปี ซึ่งอาจเป็นอัตราเงินเฟ้อหรืออัตราดอกเบี้ยของการลงทุนที่แข่งขันกัน
-
Value1 คือต้นทุนเริ่มต้นของการลงทุนหนึ่งปีนับจากวันนี้
-
Value2 คือผลตอบแทนจากปีแรก
-
Value3 คือผลตอบแทนจากปีที่สอง
-
Value4 คือผลตอบแทนจากปีที่สาม
-
Value5 คือผลตอบแทนจากปีที่สี่
-
Value6 คือผลตอบแทนจากปีที่ห้า
ในตัวอย่าง คุณไม่รวมค่าใช้จ่าย $40,000 เริ่มต้นเป็นหนึ่งในค่า เนื่องจากการชําระเงินจะเกิดขึ้นเมื่อเริ่มต้นช่วงเวลาแรก
|
อัตรา |
ค่า 1 |
ค่า 2 |
ค่า 3 |
ค่า 4 |
ค่า 5 |
ค่า 6 |
สูตร |
คำอธิบาย (ผลลัพธ์) |
|---|---|---|---|---|---|---|---|---|
|
8% |
-40000 |
8000 |
9200 |
10000 |
12000 |
14500 |
=NPV(Rate, [Value2], [Value3], [Value4], [Value5], [Value6])+[Value1] |
มูลค่าปัจจุบันสุทธิของการลงทุนนี้ (1,922.06) |
|
8% |
-40000 |
8000 |
9200 |
10000 |
12000 |
14500 |
=NPV(Rate, [Value2], [Value3], [Value4], [Value5], [Value6], -9000)+[Value1] |
มูลค่าปัจจุบันสุทธิของการลงทุนนี้ โดยขาดทุนในปีที่หกของ 9000 (-3,749.47) |