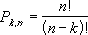บทความนี้จะอธิบายเกี่ยวกับไวยากรณ์ของสูตรและการใช้ฟังก์ชัน PERMUT ใน Microsoft Excel
คำอธิบาย
ส่งกลับจํานวนวิธีการเรียงสับเปลี่ยนตามจํานวนวัตถุที่กําหนดซึ่งสามารถเลือกได้จากวัตถุจํานวนหนึ่ง วิธีการเรียงสับเปลี่ยนคือชุดหรือชุดย่อยของวัตถุหรือเหตุการณ์ที่ลําดับภายในมีความสําคัญ วิธีการเรียงสับเปลี่ยนจะแตกต่างจากการรวมกันซึ่งลําดับภายในไม่สําคัญ ใช้ฟังก์ชันนี้สําหรับการคํานวณความน่าจะเป็นแบบลอตเตอรี
ไวยากรณ์
PERMUT(number, number_chosen)
ไวยากรณ์ของฟังก์ชัน PERMUT มีอาร์กิวเมนต์ดังนี้
-
หมายเลข จำเป็น จํานวนเต็มที่อธิบายจํานวนวัตถุ
-
Number_chosen จำเป็น จํานวนเต็มที่อธิบายจํานวนวัตถุในการเรียงสับเปลี่ยนแต่ละวิธี
ข้อสังเกต
-
อาร์กิวเมนต์ทั้งสองจะถูกปัดให้เป็นจำนวนเต็ม
-
ถ้า number หรือ number_chosen ไม่ใช่ตัวเลข ฟังก์ชัน PERMUT จะส่งกลับ #VALUE! เป็นค่าความผิดพลาด
-
ถ้า number ≤ 0 หรือถ้า number_chosen < 0 ฟังก์ชัน PERMUT จะส่งกลับ #NUM! เป็นค่าความผิดพลาด
-
ถ้า number < number_chosen ฟังก์ชัน PERMUT จะส่งกลับ #NUM! เป็นค่าความผิดพลาด
-
สมการสำหรับจำนวนวิธีการเรียงสับเปลี่ยนคือ
ตัวอย่าง
คัดลอกข้อมูลตัวอย่างในตารางต่อไปนี้ และวางในเซลล์ A1 ของเวิร์กชีต Excel ใหม่ สำหรับสูตรที่จะแสดงผลลัพธ์ ให้เลือกสูตร กด F2 แล้วกด Enter ถ้าคุณต้องการ คุณสามารถปรับความกว้างของคอลัมน์เพื่อดูข้อมูลทั้งหมดได้
|
ข้อมูล |
คำอธิบาย |
|
|
100 |
จำนวนวัตถุ |
|
|
3 |
จำนวนวัตถุในแต่ละการเรียงสับเปลี่ยน |
|
|
สูตร |
คำอธิบาย |
ผล ลัพธ์ |
|
=PERMUT(A2,A3) |
วิธีการเรียงสับเปลี่ยนที่เป็นไปได้สำหรับอาร์กิวเมนต์ที่ระบุใน A2:A3 |
970200 |
|
=PERMUT(3,2) |
วิธีการเรียงสับเปลี่ยนที่เป็นไปได้สำหรับกลุ่มที่มี 3 วัตถุโดยมี 2 วัตถุถูกเลือกไว้ |
6 |